多元统计分析R语言建模| 11 多维标度法MDS

定义：利用客体间相似性数据去解释它们之间的空间关系的统计分析方法
多维变量——二维三维空间表示，标度到低维空间上
种类：
- 度量化模型：相似性数据游距离、比例尺度测得
- 非度量化模型：顺序量表（有序）水平的相似数据
MDS的古典解
- 欧式型距离阵及其判定定理
- 距离矩阵构造A矩阵 *-0.5*d^2
- B=(bij)
- 求B的特征根，若>=0，则说明B是欧式型距离矩阵，得到的特征根是古典解
Shepard-Kruskal算法
计算步骤：
- 确定研究目的
- 选择样品和变量
- 计算样品间的距离矩阵
- 分析样品间的距离矩阵
- 计算距离阵的古典解
- 检验模型的拟合效果

#美国十个城市间公路的距离阵
d12.1=read.table('clipboard',header = T)
D=matrix(c(0,1,sqrt(3),2,sqrt(3),1,1,
           1,0,1,sqrt(3),2,sqrt(3),1,
           sqrt(3),1,0,1,sqrt(3),2,1,
           2,sqrt(3),1,0,1,sqrt(3),1,
           sqrt(3),2,sqrt(3),1,0,1,1,
           1,sqrt(3),2,sqrt(3),1,0,1,
           1,1,1,1,1,1,0),nrow=7,ncol=7)      
D
cmdscale(D)
round(cmdscale(D),3)

#MDS的古典解，线性
d12.1
MDS1=cmdscale(d12.1)
MDS1
plot(MDS1[,1],MDS1[,2],type='n',asp=1)           # asp=1确保欧氏距离正确显示
text(MDS1[,1],MDS1[,2],labels=rownames(d12.1))

#非度量化模型，非线性
#Shepard-Kruskal算法
library('MASS')
D=as.matrix(d12.1)
MDS2=isoMDS(D,k = 2)
MDS2

x=MDS2$points[,1]; 
y=MDS2$points[,2]   #降维后的两维度数据
plot(x,y,type="n")    #降维数据作散点图
text(x,y,labels=rownames(D))   #标记各点对应地区

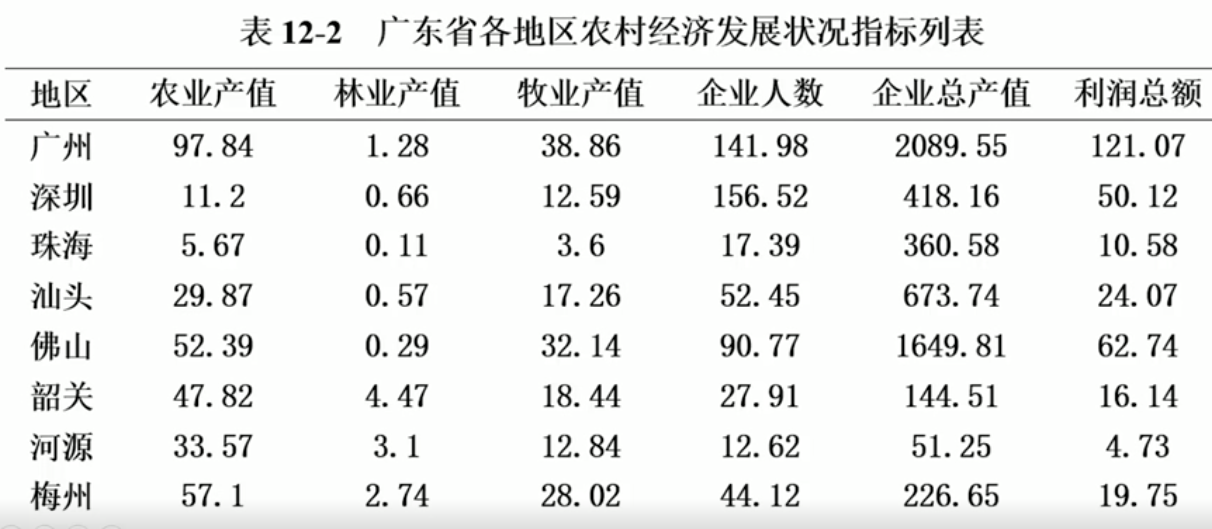
#广东省各地区农村发展状况评价分析
d12.4=read.table('clipboard',header = T)
D=dist(d12.4)
MDS3=isoMDS(D)
MDS3

x=MDS3$points[,1]; 
y=MDS3$points[,2]   #降维后的两维度数据
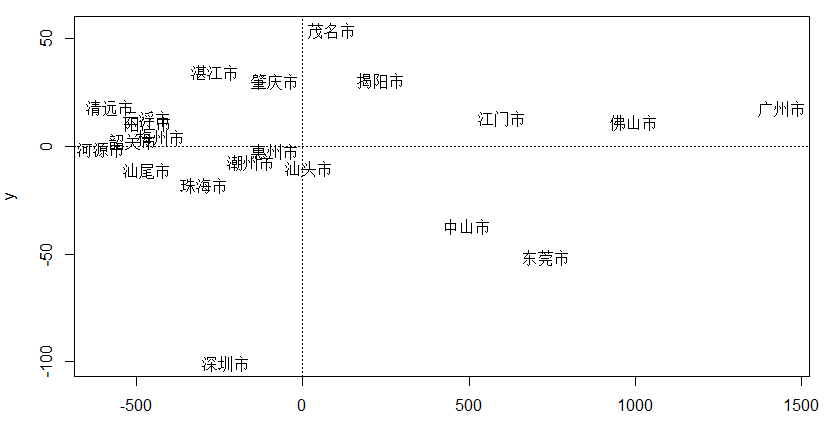
plot(x,y,type="n")    #降维数据作散点图
abline(h=0,v=0,lty=3)
text(x,y,labels=rownames(d12.4))   #标记各点对应地区

来源：oschina

链接：https://my.oschina.net/jiangroubao/blog/3231326

标签

R语言