POJ - 1426 (Find The Multiple )

题意：给定一个整数 n (<=200) 求它的一个倍数 m ，m全部由 1 或 0 组成；

 

分析：这题有三种解法；

①打表，预先处理出1~200的所有答案；

②因为答案最多只有18位，所以可以用BFS队列维护，数据用 long long 存就好；

③线段树思想；

前面两种应该很好想，说说第三种，我们以 n=6 为例子，则可以模拟一下求解过程；

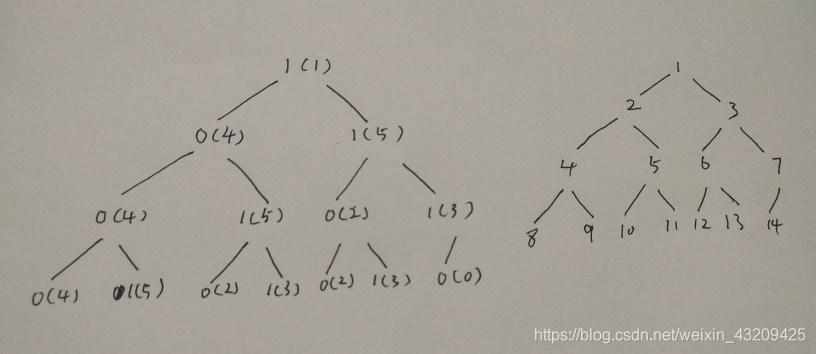
先要知道同余模定理：

(a*b)% n = (a%n*b%n)%n

(a+b)%n = (a%n+b%n)%n

所以我们每次选择当前位之后都可以只留下取模之后的数：

左边的数每一个节点 a(b) 代表当前位置选择 a 后模上 n 的余数是 b；右边则是每个节点对应的线段树编号；

可以看出，我们每次先选 0 再选1 ，对应的线段树编号则是偶数为 0 ，奇数为 1 ； 这样我们可以模拟维护一个线段树找出答案；

 

代码：

#include<queue>
#include<cstdio>
#include<iostream>
using namespace std;

int mod[1000000+10];
int n;
int ans[100];

int main()
{
    while(~scanf("%d",&n)&&n){
    	mod[1]=1%n;
    	int i;
        // i 是模拟线段树节点编号
    	for(i=2;;i++){  
    		mod[i]=(mod[i/2]*10+i%2)%n;
    		if(mod[i]==0) break;
		}
		int m=0;
		while(i){
			ans[m++]=i%2;  //偶数是0，奇数是1
			i>>=1;
		}
		while(m--){
			printf("%d",ans[m]);
		}
		puts("");
	}
} 

参考博客：(https://blog.csdn.net/lyy289065406/article/details/6647917)

来源：CSDN

作者：伴君

链接：https://blog.csdn.net/weixin_43209425/article/details/104572730