蓝桥杯 算法提高 最大值路径Python实现（动态规划）

资源限制
时间限制：1.0s 内存限制：256.0MB
问题描述
　　刷微博，编程序。如下图所示，@北京发布 提出了如下“头脑震荡”问题。对此问题做一般化描述：
　　有n阶方阵，从矩阵的左下角元素为起点，从行或列（水平或垂直）两个方向上移动，直到右上角。求出有多少条路径可以使得经过的元素累加值最大，最大值是多少。
　　

输入格式
　　共有n+1行。
　　第一行整数n，表示矩阵的阶数，2<=n<=10。
　　第二行起，每行n个整数，以空格分隔，共n行。。
输出格式
　　一行，两个空格分隔的数，第一个表示最大值路径的条数，第二个表示最大值。
样例输入
5
4 5 4 5 6
2 6 5 4 6
2 6 6 5 2
4 5 2 2 5
5 2 5 6 4
样例输出
3 47

分析：
最大的路径肯定是要动态规划出来，我直接在输入的数组上面动态规划的，直接给出题给例子动规之后的结果：

[17, 31, 35, 40, 47]
[13, 26, 31, 35, 41]
[11, 20, 26, 31, 33]
[9, 14, 16, 20, 27]
[5, 7, 12, 18, 22]

最左上角的数字就是最大的路径值。
需要我们搞定的是路径的数量。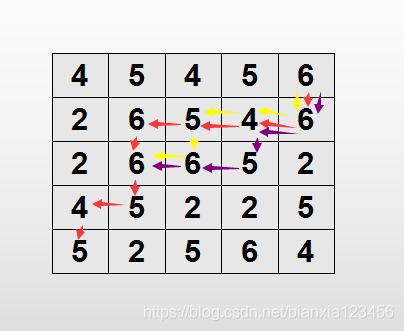

就是从数组的右上角开始往下搜索，遇到左侧下方和正下方的数字一样的时候会兵分两路，就是路径数会加一。
但是代码只能通过60%，后面的案例过不了。
后来我把搜索的数组换成动态规划之后的，就可以了，因为我们要看整体的最大步数，而不是每一步的。

AC代码：

while True:
    try:
        n = int(input())
        s = []
        for i in range(n):
            s.append(list(map(int,input().split())))   #完成输入
        ans = s[n-1][0]
        temp = []
        res = 1

        def road(i, j):
            global res
            if i == n - 1 or j == 0:  #到左边最后一列或者下面最后一行，就出来
                return
            elif s[i + 1][j] < s[i][j - 1]:
                road(i, j - 1)
            elif s[i + 1][j] > s[i][j - 1]:
                road(i + 1, j)
            else:
                res += 1
                road(i, j - 1)
                road(i + 1, j)

        for i in range(1,n):
            s[n-1][i] += s[n-1][i-1]
        for i in range(n-2,-1,-1):
            s[i][0] += s[i+1][0]
        for i in range(n-2,-1,-1):
            for j in range(1,n):
                s[i][j] += max(s[i+1][j],s[i][j-1])
        road(0, n - 1)
        print(res, s[0][n-1])
    except:
        break

编程小白记录成长

来源：CSDN

作者：干啥啥不会～

链接：https://blog.csdn.net/bianxia123456/article/details/104569574