时间复杂度O(nlogn),但是空间复杂度O(n).

算法

递归的将前半部分数据和后半部分数据各自归并排序

1.申请空间，使其大小为两个已经排序序列之和，该空间用来存放合并后的序列。
2.设定两个指针left[0]和right[0]，最初位置分别为两个已经排序序列的起始位置。
3.比较两个指针所指向的元素，选择相对小的元素pop出来，append到合并空间，并移动指针到下一位置（因为用了pop函数，所以下一位置是新的left[0或right[0]).
4.重复步骤 3 直到某一指针达到序列尾，将另一序列剩下的所有元素直接复制到合并序列尾。

算法分析

采用了经典的分治策略，它将问题分成一些小的问题然后递归求解，而治的阶段则将分的阶段解得的各个答案修补到一起。

图解

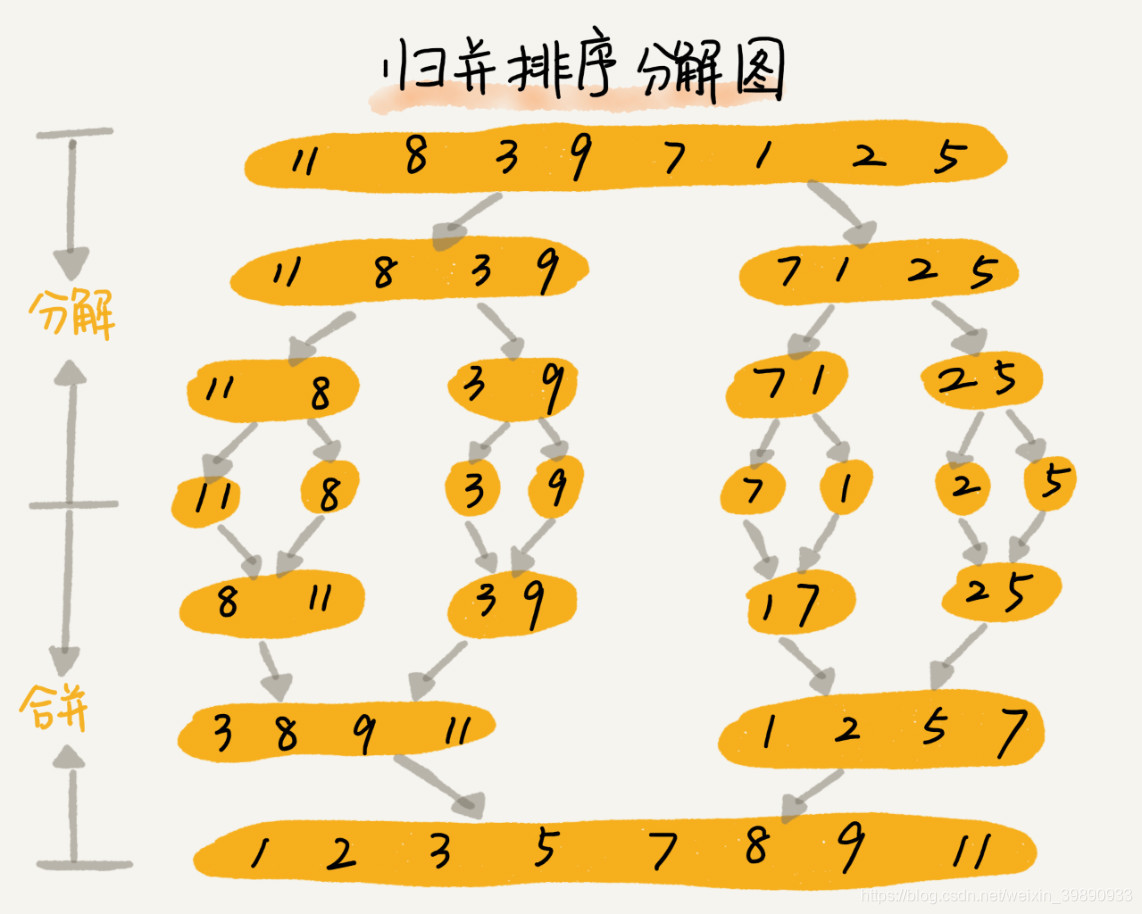
在这里插入图片描述

代码

这里我们定义两个函数，一个用于递归的进行排序，另一个用于合并两个已经排序的部分。

import math         #用到math.floor函数 向下取整
def mergesort(arr):        #递归的拆分排序
    if len(arr)<2:
        return arr
    mid=math.floor(len(arr)/2)
    left=arr[0:mid]
    right=arr[mid:]
    a=mergesort(left)
    b=mergesort(right)
    return merge(a,b)

def merge(left,right):      #用于合并已排序数组
    re=[]
    while left and right:
        if left[0]<=right[0]:
            re.append(left.pop(0))
        else:
            re.append(right.pop(0))
    while left:
        re.append(left.pop(0))
    while right:
        re.append(right.pop(0))
    return re


#实例化
array=[3,4,23,64,423,2,342,5353]
print(mergesort(array))

输出：

[2, 3, 4, 23, 64, 342, 423, 5353]

来源：CSDN

作者：qjy82

链接：https://blog.csdn.net/weixin_39890933/article/details/104471736

标签

归并排序

排序算法

arr