数据结构
一、线性表
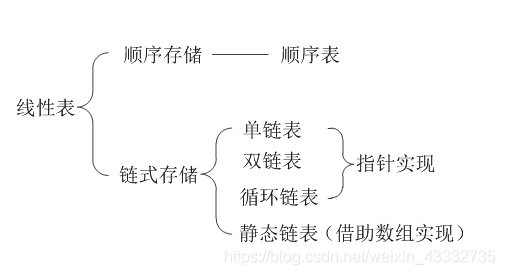
1. 顺序存储结构(顺序表)
一个线性表是n个具有相同特性的数据元素的有限序列。数据元素是一个抽象的符号,其具体含义在不同情况下不同。
2. 链表
链表里面节点的地址不是连续的,而是通过指针进行链接的。
二、哈希表
1. 哈希的导入
数组的特点是:寻址容易,插入和删除困难;
链表的特点是:寻址困难,插入和删除容易。
那么,我们综合两者的特性,做出一种寻址容易,插入和删除也容易的数据结构,这就是哈希表。
下面是哈希表的一种实现方法:拉链法。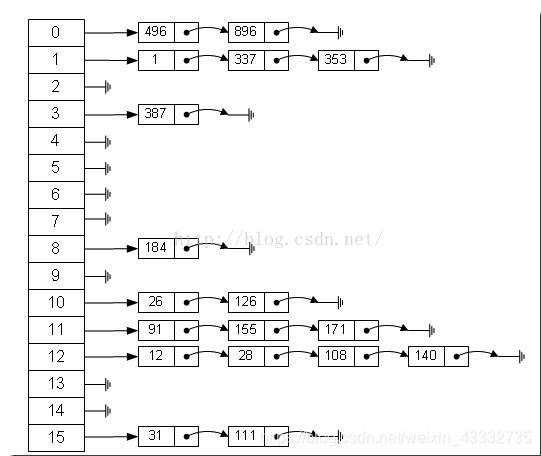
在图的左边是一个数组,数组的每个成员包括一个指针,指向一个链表的头,根据元素的特征将元素分配到不同的链表中去,我们也是根据这些特征,找到正确的链表,再从链表中找到正确的元素。
2. 哈希表
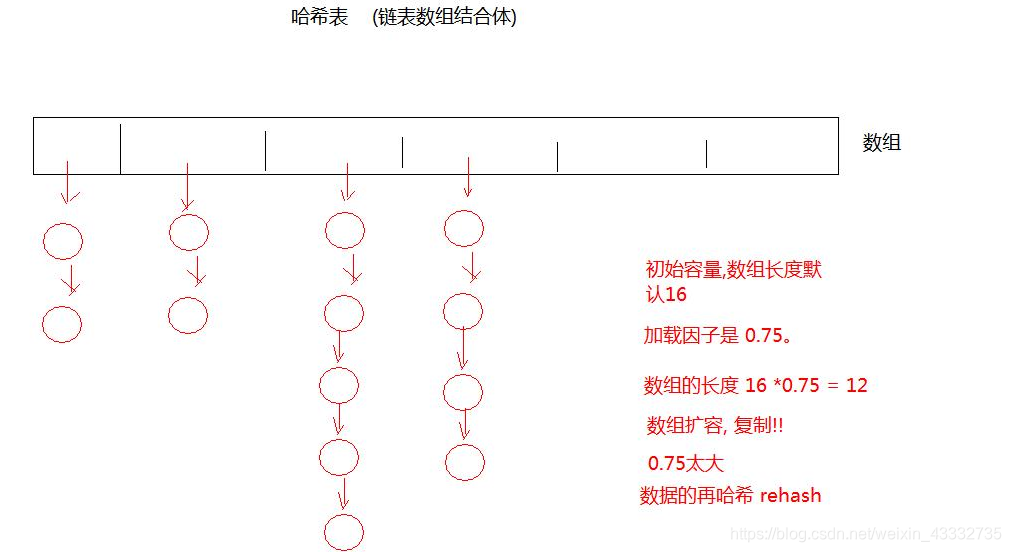
哈希表就是把Key通过一个固定的算法函数——哈希函数,转换成一个整形数字,然后就将该数字对数长度进行取余,取余结果当作数组的下标,将value存储在以该数字为下表的数组空间里。
3. 哈希表的优缺点
优点
- 时间少:无论哈希表中的数据量,我们在操作时的插入,删除,查询都只需要O(1)的时间级。
- 速度快:在日常程序中,在特定时间内哈希表的查找速度总比树快。
- 编程简单:相对树来讲,哈希表编程实现相对简单。
缺点
- 哈希表基于数组,数组创建后难以扩展,故当哈希表被基本填满时,性能下降会非常严重,所以在创立哈希表时我们必须清楚表中将要存储多少数据。
三、数组
采用一段连续存储单元来存储数据。
数组对于指定下标的查找,时间复杂度为O(1);
通过给定值进行查找,需要遍历数组,时间复杂度为O(n);
对于有序数组,可采用二分查找、插值查找、斐波那契查找等方式,将时间复杂度提升为O(logn);
对于一般的删除操作,其时间复杂度为O(n)。
三者的区别
| 基本数据结构 | 优点 | 缺点 |
|---|---|---|
| 数组 | 随机访问效率高;搜索效率高。 | 内存连续且固定,存储效率低;插入和删除效率低。 |
| 链表 | 不要求连续内存,内存利用率高;插入和删除效率高。 | 不支持随机访问;搜索效率低 |
| Hash表 | 搜索效率高;插入和删除效率高 | 内存利用率低;存在散列冲突 |
集合类的基本概念
1. 泛型
Java重要概念,在集合内应用广泛。
集合的元素,可以是任意类型对象的引用,如果把元素放入集合,则会忽略它的类型,把它当作Object类型处理。
但由于Object所描述的数据类型过大,在实际使用中就会数据类型不匹配而出现传入数据类型错误,从而引发ClassCastException异常,且这类错误在编译时不会告诉开发者,实际运行中才会产生安全隐患。
泛型可以在编译时检测出程序的安全隐患,增加程序的健壮性。
泛型则规定了某个集合只能存放特定类型对象的引用,会在编译期间进行类型检查,可以直接指定类型来获取集合元素。
泛型的核心数据思想是:类中的属性或方法的参数与返回值的类型采用动态标记,在对象实例化的时候动态地配置要使用的数据类型。
注意:泛型只允许设置引用数据类型。
//定义
class Point<T>{// 此处可以随便写标识符号
private T x ;
private T y ;
public void setX(T x){//作为参数
this.x = x ;
}
public void setY(T y){
this.y = y ;
}
public T getX(){//作为返回值
return this.x ;
}
public T getY(){
return this.y ;
}
};
//IntegerPoint使用
Point<Integer> p = new Point<Integer>() ;
p.setX(new Integer(100)) ;
System.out.println(p.getX());
//FloatPoint使用
Point<Float> p = new Point<Float>() ;
p.setX(new Float(100.12f)) ;
System.out.println(p.getX());
泛型的好处:
- 提高了安全性(将运行期的错误转到编译期)。
- 省去了强制转换。
2.哈希值
-
就是一个十进制的整数,有操作系统随机给出
-
可以使用
Object类中的方法hashCode获取哈希值 -
Object中源码:int hashCode()返回该对象的哈希码值;
3.平衡二叉树(AVL树)
平衡二叉树的特点是左右子树高度差的绝对值不超过1,且左右两个子树都是一棵平衡二叉树。
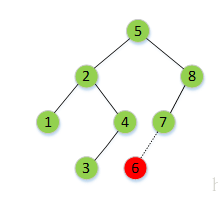
如上图,如果插入6这一元素, 则8的左子树深度就为2, 右子树深度就为0,绝对值就为2, 就不是一个平衡二叉树。
4. 红黑树
红黑树是一种自平衡的二叉查找树。它的检索效率是O(log n)
红黑树的几大特点:
- 每个节点要么是红的要么是黑的。
- 根节点是黑的。
- 每个叶节点都是黑的。(叶节点指树尾端NIL指针或NULL节点)
- 如果一个节点是红的,那么它的两个儿子是黑的。(反之不一定)
- 对于任意节点而言,其到叶节点树尾端NIL指针的每条路径都包含相同数目的黑节点。
来源:CSDN
作者:木头人i
链接:https://blog.csdn.net/weixin_43332735/article/details/104474400