最小生成树–prim算法

应用背景：
	最节省经费的前提下，在n个城市之间建立通信联络网
	定点表示城市
	边表示城市之间的线路
	边的权值表示相应的代价

生成树的代价：树上各边权值之和
最小代价生成树（Minimum Cost Spanning Tree,简称最小生成树）
无相连通网的最小代价生成树

左边的就是连通图，右边的就是最小代价生成树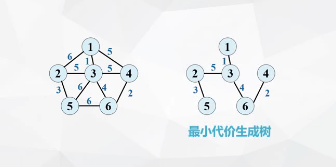
在这里插入图片描述
一个连通图的最小生成树不一定唯一，但最小生成树的代价（权值之和）一定是相同的

构造最小生成树有多种算法，其中多数利用了最小生成树的MST性质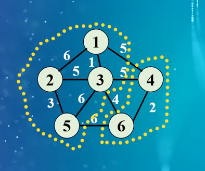
在这里插入图片描述
在这个图中我们去任意划分这个图的两个集合，一定存在某个边跨越这两个数的集合，这条边一定是在我们最小生成树上面

MST性质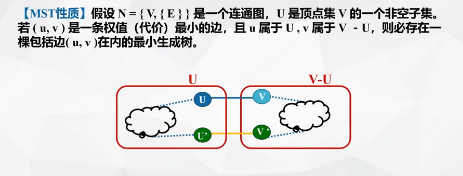
在这里插入图片描述

树的概念：只要在树的任意一条加上一条边，一定会产生回路

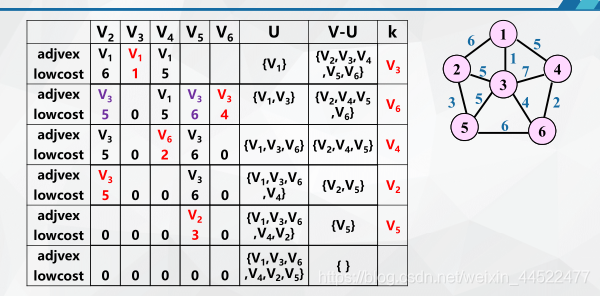
Prim算法

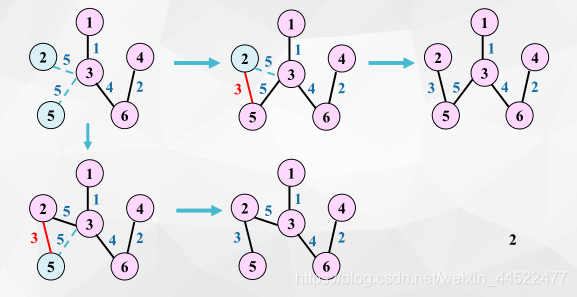
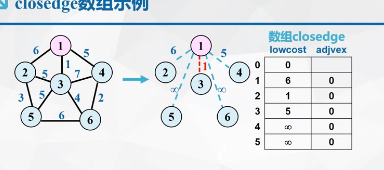
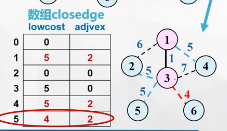
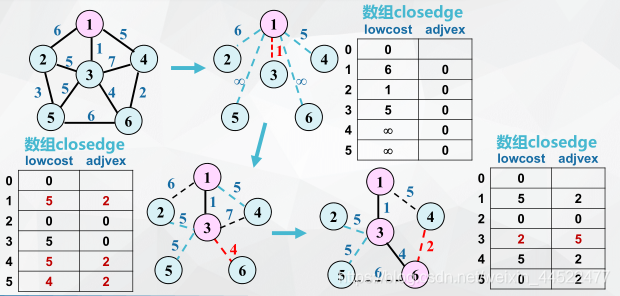
在这里插入图片描述

closedge数组

附设一个辅助数组closedge,用记录从V-U的各个顶点到U的具有最小代价的边

对每个顶点vi属于V-U,相应的分量为closedge[i-1],它包括两个域：
1.lowcost存储该边上的权，即
	closedge[i-1].lowcost=min{cost(u,vi)|u∈U}
	网用领接矩阵表示法
2.Adjvex存储该边依附的在U中的顶点
	U中每增加一个顶点，只要考虑该新增顶点到vi的这条边上的权值会不会更小即可