图论中的经典问题:给一个图,求出起点到终点的最短路径。
Graph Representation
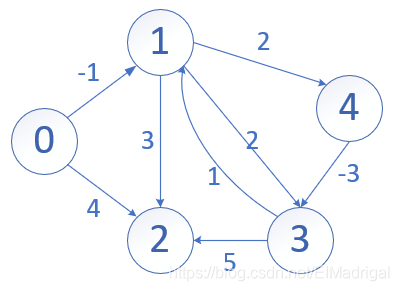
- adjacency matrix
| i/j | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| 0 | \(\infty\) | -1 | 4 | \(\infty\) | \(\infty\) |
| 1 | \(\infty\) | \(\infty\) | 3 | 2 | 2 |
| 2 | \(\infty\) | \(\infty\) | \(\infty\) | \(\infty\) | \(\infty\) |
| 3 | \(\infty\) | 1 | 5 | \(\infty\) | \(\infty\) |
| 4 | \(\infty\) | \(\infty\) | \(\infty\) | -3 | \(\infty\) |
用vector<vector<int>> g(n, vector<int>(n, INF))表示,g[i][j]表示从顶点\(i\)到顶点\(j\)的权重,空间复杂度\(O(|V|^2)\),适用于稠密图,用的不多;
- adjacency list
链表比较少用,基本都用动态数组:
| 0 | (1,-1) | (2,4) | - | - | - |
|---|---|---|---|---|---|
| 1 | (2,3) | (3,2) | (4,2) | - | - |
| 2 | - | - | - | - | - |
| 3 | (1,1) | (2,5) | - | - | - |
| 4 | (3,-3) | - | - | - | - |
用vector<vector<pair<int, int>>> g表示,g[i][j].first表示从顶点\(i\)出发到达的顶点\(k\),g[i][j].second表示从顶点\(i\)到顶点\(k\)的权值,空间复杂度\(O(|V|+|E|)\)。
edge list
(0,1,-1),(0,2,4),(1,2,3),(1,3,2),(1,4,2),(3,1,1),(3,2,5),(4,3,-3)
用vector<vector<int>> e表示,e[i][0]表示顶点\(u\),e[i][1]表示顶点\(v\),e[i][2]表示\(u\)到\(v\)的权值,空间复杂度\(O(|E|)\)。Dijkstra
单源最短路径算法,只能用于所有边权值为正的图,本质上还是贪心,思想:
- 将所有结点分为两类:已经确定最短路径的点集\(u\)、未确定最短路径的点\(v\);
- 初始化\(dis[start]=0\),其余结点\(dis\)设为无穷大;
- 找出一个\(dis\)最小的\(v\)中的点\(x\),将其标记为\(u\),遍历\(x\)的所有出边,若\(dis[y]>dis[x]+weight\),则更新\(y\)点到源点的最短路径长度\(dis[y]=dis[x]+weight\);
- 重复,直到所有点都在\(u\)中。
/*邻接矩阵版,适合顶点比较少的图,复杂度O(V^2)*/
int vertexNum, adjMatrix[MAXN][MAXN];
int dis[MAXN]; //起点到各点最短路径长度
bool visited[MAXN] = {false};
void Dijkstra(int start)
{
for (int i = 0; i < vertexNum; i++)
{
dis[i] = INFINITY;
}
dis[start] = 0;
for (int i = 0; i < vertexNum; i++)
{
//寻找未访问点中dis最小的
int u = -1, minDis = INFINITY;
for (int j = 0; j < vertexNum; j++)
{
if (visited[j] == false && dis[j] < minDis)
{
u = j;
minDis = dis[j];
}
}
if (u == -1) //剩余的点与起点不连通
return;
visited[u] = true;
//以u为中介试图优化dis[j]
for (int j = 0; j < vertexNum; j++)
{
//未访问、u可达、路过u可以使dis[j]更优
if (visited[j] == false && adjMatrix[u][j] != INFINITY && dis[u] + adjMatrix[u][j] < dis[j])
dis[j] = dis[u] + adjMatrix[u][j];
}
}
}
/*邻接表版,复杂度O(V^2+E)*/
int vertexNum;
int dis[MAXN]; //dis[i]表示源点到i点的最小距离
bool visited[MAXN] = {false};
struct Edge{
int des; //边的目标顶点
int weight; //边的权值
};
vector<Edge> adjList[MAXN]; //邻接表
void dijkstra(int start)
{
for(int i = 0;i < vertexNum;i++)
{
dis[i] = INT_MAX;
}
dis[start] = 0;
for(int i = 0;i < vertexNum;i++)
{
int u = -1,minDis = INT_MAX;
for(int j = 0;j < vertexNum;j++)
{
if(visited[j] == false && dis[j] < minDis)
{
u = j;
minDis = dis[j];
}
}
if(u == -1)
return;
visited[u] = true;
for(int j = 0;j < adjList[u].size();j++)
{
//直接获得u能到达的点
int v = adjList[u][j].des;
if(visited[v] == false && dis[v] > dis[u] + adjList[u][j].weight)
{
dis[v] = dis[u] + adjList[u][j].weight;
}
}
}
}
寻找\(dis[u]\)的循环可以用堆来优化,使得复杂度降为\(O(VlogV+E)\)。
Bellman-Ford
可以计算含有负权的边,检测是否存在一个从源结点可以到达的权重为负值的环路(负权环):
bool bellmanFord(vector<vector<int>>& edge, vector<int>& dis, int start) {
for (int i = 0; i < dis.size(); ++i) {
if (i == start)
dis[i] = 0;
else
dis[i] = 0x3f3f3f3f;
}
for (int i = 0; i < dis.size(); ++i)
for (int j = 0; j < edge.size(); ++j)
dis[edge[j][1]] = min(dis[edge[j][1]], dis[edge[j][0]] + edge[j][2]);
bool negCycle = false;
for (int i = 0; i < edge.size(); ++i)
if (dis[edge[i][1]] > dis[edge[i][0]] + edge[i][2]) {
negCycle = true;
break;
}
return negCycle;
}
复杂度\(O(VE)\)。
Floyd-Warshall
多源最短路径算法。
void floyd(vector<vector<int>>& m) {
for(size_t k = 0;k < m.size();++k)
for(size_t i = 0;i < m.size();++i)
for (size_t j = 0; j < m.size(); ++j) {
// m不能用INT_MAX初始化,会溢出,用0x3f3f3f3f
if (m[i][k] + m[k][j] < m[i][j])
m[i][j] = m[i][k] + m[k][j];
}
}
不能用于含有负权环的图,这种图不存在最短路径。
来源:https://www.cnblogs.com/EIMadrigal/p/12328847.html