误差回传神经网络(BP)
BP网络是一种无反馈的前向网络,网络中的神经元分层排列,每一层内的神经元的输出均传送到下一层,这种传送由联接权来达到输出的作用。工作过程分为学习期和工作期两个部分,计算关键在于学习期中的误差反向传播过程,使目标函数最小化来完成的。
1) BP神经网络的设计
如图1为BP神经网络基本结构图。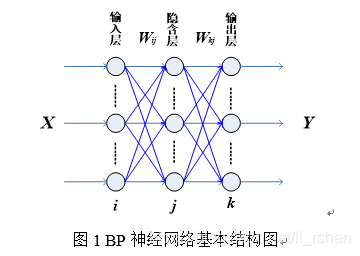
输入层、隐含层、输出层神经元分别以 予以编号。
具体的计算公式如下:
隐含层与输出层的各个神经元的输入分别为
隐含层与输出层的各个神经元的输出分别为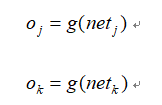
其中激活函数 均为单极性 Sigmiod函数,即: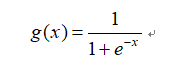
2)计算网络误差
网络的输出 与实际输出 (期望值)不相等时,存在训练的误差,则系统的平均误差为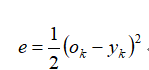
网络的总误差表示为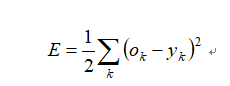
上式便是BP神经网络的目标函数,学习期中的误差反向传播过程,就是使目标函数最小化来完成的。
3)各层权值的调整
每一层的权值的调整都是反向的一个过程,也就是说由实际输出值yk与实际相比得到的误差信号δ_k ,对隐含层与输出层之间的权重 w_kj进行调整。
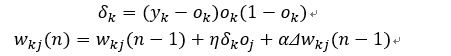
然后由误差信号 反向传至输入层,得到输入层误差信号 ,由此起到对输入层与隐含层之间的权值调整。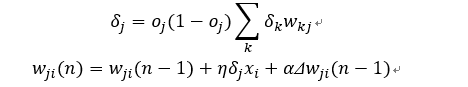
其中η 为学习率,α 为动量项,以此提高BP神经网络的训练速度,且能够保持一定的稳定性。
通过网络训练,达到要求后,网络各个节点之间的互联权值就完全确定,则称整个的BP网络已经学习好。
模型建立
确定BP神经网络的参数。
常见的BP神经网络为三层,分别为输入层、隐含层、输出层。其中输入层、输出层神经元的个数根据实际确定,而隐含层的神经元个数的确定可以依旧原则:隐含层的神经元个数大于输入输出层神经元个数和的一半,小于输入输出层神经元个数的和。
定义目标函数为式,影响训练的学习效率的学习率η∈(0,1) 和动量项 α∈(0,1)。
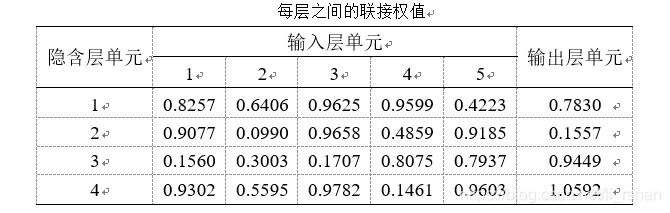
网络训练得到每一层之间的联接权值。
模型的各个参数确定后,将训练样本进行训练,当所有的训练样本训练结束后,得到输入层与隐含层、隐含层与输出层之间的联接权值。
训练的过程如下图2。
计算权重
(孙会君,王新华.应用人工神经网络确定评价指标的权重[J].山东科技大学学报(自然科学版),2001,20(3):84-86.)
对各个层之间的联接权值采用显著关联系数法分析个指标对全局可信度的影响程度,做归一化处理,可求得输入输出之间的关系,即指标的权向量 。
归一化公式为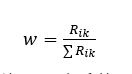
其中 R_ik为显著关联系数法中的绝对影响系数。
BP算法训练流程图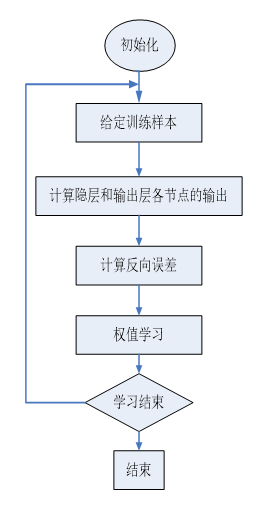
来源:https://blog.csdn.net/li_rshan/article/details/99691951