面试题7：重建二叉树

题目：输入某二叉树的前序遍历和中序遍历的结果，请重建该二叉树，假设输入的前序遍历和中序遍历的结果都不含重复的数字。例如：输入前序遍历序列{1,2,4,7,3,5,6,8}和中序遍历序列{4,7,2,1,5,3,8,6}则重建二叉树。

二叉树：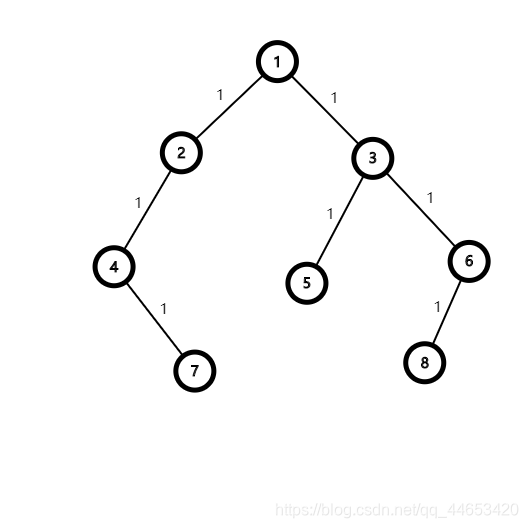

算法思路：

1. 确定二叉树的根节点：先序序列的第一个数字就是根结点的值
2. 确定左子树以及右子树：在中序序列中找到根节点，在根节点之前的都是左子树节点，在根节点之后的都是右子树节点
3. 递归以上两步

关键点：算法中及其重要的是，找到中序序列中根节点的位置，继而确定左右子树长度以及函数参数。

代码如下：

#include<iostream>
#include<exception>
using namespace std;

typedef struct Binarytree
{
	int data;
	Binarytree *lchild;
	Binarytree *rchild;
}tree;

tree* Construct(int *preorder,int *inorder,int length);
tree* ConstructCore(int *startPreorder,int *endPreorder,int *startInorder,int *endInorder);
void printBT(const std::string &prefix, tree *&node, bool isLeft) ;
void print(tree *node);


tree* Construct(int *preorder,int *inorder,int length)
{
	if(preorder == NULL || inorder == NULL || length < 0)
	{
		return NULL;
	}
	
	return ConstructCore(preorder,preorder + length - 1,inorder,inorder + length  - 1);
}
 
 
tree* ConstructCore(int *startPreorder,int *endPreorder,int *startInorder,int *endInorder)
{
	//创建根节点
	int rootvalue = startPreorder[0];
	tree* root  = new tree();
	root->data = rootvalue;
	root->lchild = root->rchild = NULL;
	
	
	//检查先序与中序字符串 
	if(startPreorder == endPreorder)
	{
		if(startInorder == endInorder && *startPreorder == *startInorder)
		{
			return root;//长度为一且相等 返回根节点 
		}
		else
		{
			cout<<"error！"<<endl;
		} 
	}
	
	//在中序遍历中找到根节点的值  
	//只有在找到根节点之后 才方便计算 先序序列的长度 进而计算先序序列与中序序列的起始点以及尾结点 
	int *rootInorder = startInorder;//初始化 
	while(rootInorder <= endInorder && *rootInorder != rootvalue)
	{
		++rootInorder;//循环条件 中序遍历未完成 未找到根节点 
	}
	if(rootInorder == endInorder && *rootInorder != rootvalue)
	{
		cout<<"error!"<<endl;//没找到 
	} 
	
	
	int leftLength = rootInorder - startInorder;//找出左子树的所有根节点 计算长度 （少一个） 
	int* leftPreorderEnd = startPreorder + leftLength; //左子树先序序列的尾结点。 
	
	if(leftLength > 0) 
	{
		//构建左子树 递归 
		
		//先序序列的 起始点 是原来的先序序列根节点的后面一个节点 
		//先序序列的 尾结点 是左子树长度加一 
		//中序序列的 起始点 没有变 
		//中序序列的 尾结点 根节点前面一个节点 
		
		root->lchild = ConstructCore(startPreorder + 1,leftPreorderEnd,startInorder,rootInorder - 1); 
	}
	
	if(leftLength < endPreorder - startPreorder)
	{
		//构建右子树 递归 
		
		//先序序列的 起始点 是在左子树先序序列的尾部节点的后面一个节点
		//先序序列的 尾结点 是原先二叉树的先序序列的尾结点
		//中序序列的 起始点 是在根节点后面一个节点
		//中序序列的 尾结点 是原先二叉树的中序序列的尾结点
		 
		root->rchild = ConstructCore(leftPreorderEnd + 1,endPreorder,rootInorder + 1,endInorder); 
	}
	
	return root;
}

void Test(char *testname,int *preorder,int *inorder,int length)
{
	if(testname != NULL)
	{
		cout<<"Test begins"<<endl;
	}
	
	cout<<"The preorder sequence is: ";
	for(int i = 0; i < length; ++i)
	{
		cout<<preorder[i]<<" ";
	}
	
	cout<<endl;
	
	cout<<"The inorder sequence is: ";
	for(int i = 0; i < length; ++i)
	{
		cout<<inorder[i]<<" ";
	}
	cout<<endl;
	
	try
	{
		tree *root = Construct(preorder,inorder,length);
		print(root);
	}
	catch(std::exception& exception)
	{
		cout<<"Invalid Input.\n"<<endl; 
	}
	
 } 

//改造先序遍历 打印二叉树 
void printBT(const std::string &prefix, tree *&node, bool isLeft) 
{
    if (node!= NULL)
	{
        std::cout << prefix;
        std::cout << (isLeft ? "├── " : "└── ");
        std::cout << node->data << std::endl;
        printBT(prefix + (isLeft ? "│   " : "    "), node->lchild , true);
        printBT(prefix + (isLeft ? "│   " : "    "), node->rchild , false);
    }
}
void print(tree *node)
{
    printBT("", node, false);
}

// 普通二叉树
//              1
//           /     \
//          2       3  
//         /       / \
//        4       5   6
//         \         /
//          7       8

void Test1(void)
{
	const int length = 8;
	int preorder[length] = {1,2,4,7,3,5,6,8};
	int inorder[length] = {4,7,2,1,5,3,8,6};
	
	Test("Test1",preorder,inorder,length);
}

int main(void)
{
	Test1();
	return 0;
}
 

来源：CSDN

作者：Summer&Vibe

链接：https://blog.csdn.net/qq_44653420/article/details/104277343