各种招式筛素数 | 易学教程

筛选素数方法归纳

我也不知道为什么突然好奇筛选素数，不过去查如何列举出n以内素数还是有一定原因的。有一天闲着没事干去翻了翻某佬的blog，看到有一道竞赛题是dp+筛选素数的，好奇之下就点了进去，dp思路看懂了，可这个筛素数愣是不知道什么原理，最后差不多琢磨一天才搞懂，（菜鸡警告~）。
筛素数，这一听，感觉就挺简单的，傻瓜式(无脑)的解法就是写两个for循环，然后开始遍历，i%j是否可以为0，假如可以，说明不是素数，不展开讲这种我都能想得到的东西了.

Code:

#include<bits/stdc++.h>
using namespace std;
int prime[1000];
int main(){
    int n,cnt=0,flag;
    memset(prime,0,sizeof(prime));
    prime[++cnt]=2;
    scanf("%d",&n);
    for(int i=3;i<=n;i++)
    {
        flag=1;
        for(int j=2;j<i;j++)//可以把i换成sqrt(i); 
        {
            if(i%j==0)
                flag=0; 
        }
        if(flag==1)
            prime[++cnt]=i;
    }
    printf("%d\n",cnt);
    for(int i=1;i<=cnt;i++)
        printf("%d ",prime[i]);
    return 0;
}

复杂度：O（n^2），自己想想都后怕,不过稍微改一下循环终止条件,换成j<sqrt(i)，也许好些。

不扯了不扯了，接下来先说埃拉特斯特尼筛法，主要刚开始我根本看不懂欧拉筛(小声bb)。
埃拉特斯特尼的筛法的原理主要是从2开始，将每个素数的倍数标记为合数，最后未标记的就是素数。
伟人想的，我也不知道为啥，不过我自己手动模拟了一下。

下面是一个5x5的表格，也就是说我现在要求25以内的质数有多少个.

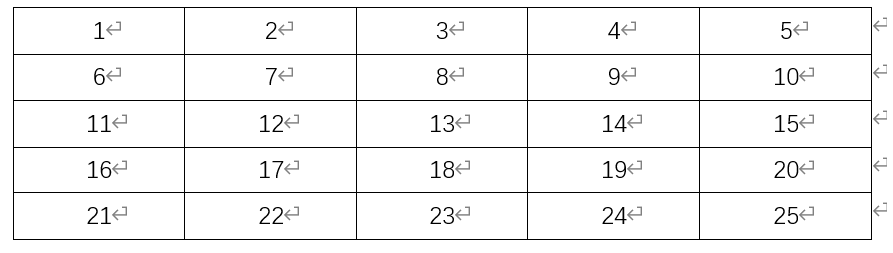
无底纹的则为素数，橙色底纹为非素数。

因为1什么都不是就先标记为不是素数咯

接着i=2开始，2为素数，这时我们开始找2的倍数（第一次找合数）.

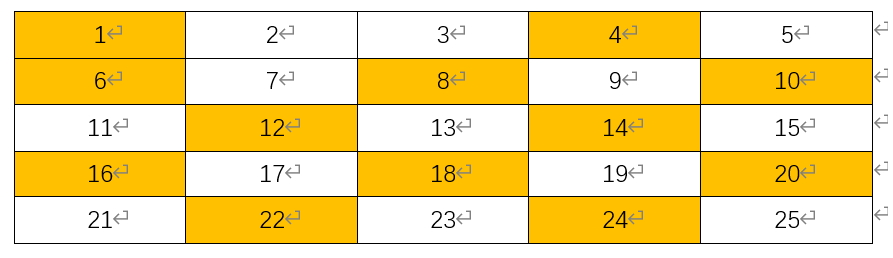
第一次素数找完，接着i++,i=3，这里说明一下，虽然说可以直接找3的倍数，但是我们可以优化一下，原因是3x2=2x3=6，6这个合数会被找第二遍，为了进行优化直接让j=i*i；
所以直接第一个kill掉的合数就是3x3=9。

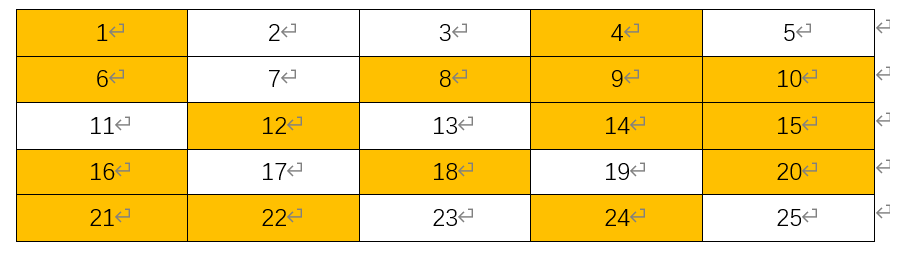
接着i++，4是合数，直接pass掉，i++，i此时为5,直接就是5x5=25，kill掉最后一个合数

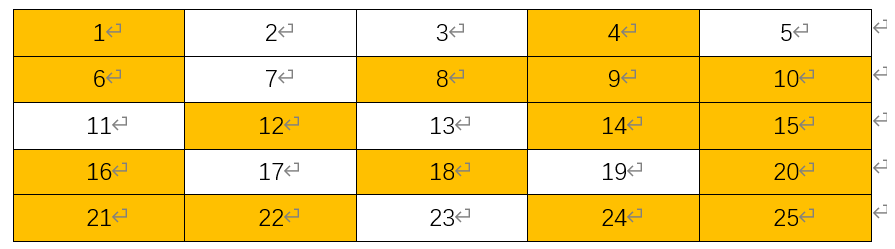
大功告成，这时候没有橙色底纹的均为素数.

Code:

#include<stdio.h>
#include<iostream>
#include<algorithm>
#include<stdlib.h>
#include<string.h>
#include<math.h>
using namespace std;
typedef long long LL;
const int maxn=1e5+7;
const int maxm=2e5+7;
const long long INF=0x3f3f3f3f;
const long long mod=1e9+7;
int vis[maxm],prime[maxm];
int n,cnt=0;
void solve()
{
    memset(vis,1,sizeof(vis)); //用vis标记1为素数 ,0不是素数. 
    for(int i=2;i<=n;i++)
    {
        if(vis[i])//判断是否为素数. 
        {
            prime[++cnt]=i;//用cnt记录素数的个数. 
            for(int j=i*i;j<=n;j+=i)
                vis[j]=0;//标记j为合数 
        }
    }
    return;
}

int main()
{
    scanf("%d",&n);
    solve();
    printf("%d\n",cnt);//前n的素数总数
    for(int i=1;i<=cnt;i++)
        printf("%d ",prime[i]);  
    return 0;
}

这种算法的复杂度为O(nloglogn)稍微好点，但是还有更好的，可以使复杂度达到O(n)。

欧拉筛法基本原理：在埃拉特斯特尼的筛法上进行优化，每个合数只被自己最小的质数筛选一次，不会被重复筛，任何的合数都可以表示为一个数与一个质数的乘积。

举个简单的例子：12这个合数会最小的质数是2，那么就会是6x2=12，而不会是4x3=12，因为2比3小。埃拉特斯特尼的缺陷就是会重复筛，例如40这个合数，在前面220=40已经kill过一次，接着58=40又kill一次，看着就有点累.

Code:

#include<stdio.h>
#include<iostream>
#include<algorithm>
#include<string.h>
#include<stdlib.h>
#include<math.h>
using namespace std;
typedef long long LL;
const int maxn=1e5+7;
const int maxm=2e5+7;
const long long INF=0x3f3f3f3f;
const long long mod=1e9+7;
int n,cnt=0;
int vis[maxm],prime[maxm];
void solve()
{
    memset(vis,1,sizeof(vis));//值为1的为素数. 
    memset(prime,0,sizeof(prime));
    for(int i=2;i<=n;i++)
    {
        if(vis[i])
            prime[++cnt]=i;
        for(int j=1;j<=cnt&&i*prime[j]<=n;j++)
        {
            vis[i*prime[j]]=0;
            if(i%prime[j]==0)
                break;
        }
    } 
}

int main()
{
    scanf("%d",&n);
    solve();
    printf("%d\n",cnt);//输出n以内的素数 
    for(int i=1;i<=cnt;i++)
        printf("%d ",prime[i]);
    return 0;
}

其实我也不知道去怎么理解，不过整体的理解可以举个例子去捋清这个算法的思路。
I其实遍历的是前n的数,然后prime[j]里面放的是素数。
循环终止条件也好理解，算出来的合数不能大于n，不然就不是求n以内的合数，j<=cnt，就不用说了，有多少个素数就用多少个，大于cnt也没有素数存在prime数组里面。
接着我看网上一些文章都给这句代码写上了注释，if(i%prime[j]==0)，说这是重点所在，
然后我就想这是什么原理，后来我觉得拿4x3=12，6x2=12这个例子理解比较生动形象，当i=4,j=1，
i x prime[j]=4x2=8,这时候4%2=0就让循环终止，假设我们循环继续，这时候j=2,i x prime[j]=4x3=12. 而当i=6的时候,6 x prime[1]=12，就重复了，也就是说只要i%prime[j]=0，i x prime[j+1]得到的合数可以被prime[j] x 某个数得到。
实在理解不了就枚举吧，暴力出奇迹。

来源：https://www.cnblogs.com/K2MnO4/p/12296496.html

标签

判断素数