马拉车 Manacher

Manacher，人称马拉车。是用来查找一个字符串的最长回文子串的线性算法。

对于一个子串长度有可能是偶数也可能是奇数。为了实现简单与准确，对原串更改。如 ababca 为 $#a#b#a#b#c#a#，令新串为 $s$。

定义 $p_i$ 为以 $i$ 为对称中心的最长回文半径。刚刚栗子的 $p$ 为

$ # a # b # a # b # c # a # 
1 1 2 1 4 1 4 1 2 1 2 1 2 1

可以发现：非字母字符对应的 $p_i$ 为奇数，字母字符对应的 $p_i$ 为偶数。在新串中，因为有其它的字符，所以以 $i$ 为中心的最长回文子串长度为 $p_{i} - 1$。那么初始化是简单明了的。

void init(){
	str[1] = '$'; str[2] = '#';
	for (int i = 1; i <= n; i++) str[i * 2 + 1] = s[i], str[i * 2 + 2] = '#';
	n = (n + 1) * 2 + 1; 
}

难点在构造 $p$，从左到右构造 $p$ 数组。令 $mx$ 为以 $id$ 为中心的最长回文子串的右边界，有 $id + p_{id} = mx$。对于当前的 $i$，如果有 $i < mx$，那么 $p_i = \min \{ p_{2 \times id - i}, mx - i\}$。

略证：令 $j$ 为 $2 \times id - i$，那么 $p_i = \min \{ p_j, mx-i \}$。有 $\frac{i + j}{2} = id$，故根据中点公式知 $id$ 为 $i$ 与 $j$ 的中点。

如下图，对于取 $p_j$ 的情况为 $i$ 与 $j$ 那一段相等。那么 $i$ 的那一段能更长吗？不能的，因为如果更长，意味着 $s_{l-1} = s_{r+1}$ 了。如果成立，有 $l-1$ 与 匹配 $l-1$ 的点相同，进而有蓝线的成立关系，蓝线成立则与 $p_j$ 已经求出矛盾。

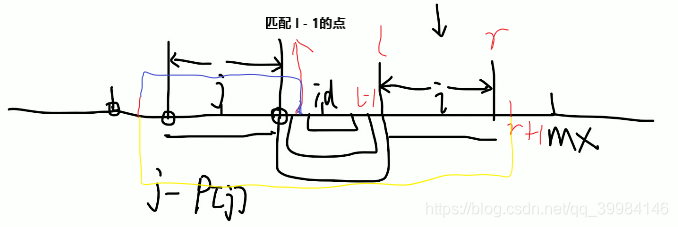
刚才讨论的情况是 $p_j$ 在 $id$ 的覆盖范围的，若超出，那么不满足限定 $i$ 与 $j$ 那一段相等。如下图，根据 $id$ 是 $i$ 与 $j$ 的中点，可知 $p_i$ 最短也是 $mx-i$，那么可能更大即为 $i$ 扩展到 $mx$ 往右呢？不能的，因为若想让蓝线成立，那么有绿线成立，进而有橙线成立，而橙线成立超出了以 $id$ 为对称中心 的 $mx$ 的边界而矛盾。

综上所述。 $p_i = \min \{ p_{2 \times id - i}, mx - i\}$，并随时更新 $id$ 与 $mx$。

void manacher(){
	int mx = 0, id = 0;
	for (int i = 2; i <= n; i++){
		if (i < mx) p[i] = min(p[id * 2 - i], mx - i);
		else p[i] = 1;
		for (; str[i + p[i]] == str[i - p[i]]; p[i]++) 
			if (p[i] + i > mx) id = i, mx = p[i] + i;
	}
}

马拉车还可用于 hash，所以不一定是字母回文，还可能是数字回文。

#include <bits/stdc++.h>
using namespace std;
#define re register
#define F first
#define S second
typedef long long ll;
typedef pair<int, int> P;
const int N = 3e7 + 1e6 + 5;
const int INF = 0x3f3f3f3f;
int read() {
	int x = 0, f = 0; char ch = 0;
	while (!isdigit(ch)) f |= ch == '-', ch = getchar();
	while (isdigit(ch)) x = (x << 3) + (x << 1) + (ch ^ 48), ch = getchar();
	return f ? -x : x;
}
int n, p[N];
char s[N], str[(N << 1) + 100];
void init(){
	str[0] = '$'; str[1] = '#';
	for (int i = 0; i < n; i++) str[(i << 1) + 2] = s[i], str[(i << 1) + 3] = '#';
	n = (n << 1) + 2;
}
void manacher(){
	int mx = 0, id = 0;
	for (int i = 1; i < n; i++){
		if (i < mx) p[i] = min(p[(id << 1) - i], mx - i);
		else p[i] = 1;
		for (; str[i + p[i]] == str[i - p[i]]; p[i]++) 
			if (p[i] + i > mx) id = i, mx = p[i] + i;
	}
}
int main(){
	scanf("%s", s); n = strlen(s);
	init(); manacher();
	int ans = 0;
	for (int i = 0; i < n; i++) ans = max(ans, p[i]);
	printf("%d\n", ans - 1);
	return 0;
}

来源：CSDN

作者：ylxmf2005

链接：https://blog.csdn.net/qq_39984146/article/details/104226062