前向星 | 易学教程

什么是前向星？

一种数据结构，以储存边的方式来存储图。构造方法如下：读入每条边的信息，将边存放在数组中，把数组中的边按照起点顺序排序(可以使用基数排序，如下面例程)，前向星就构造完了。通常用在点的数目太多，或两点之间有多条弧的时候。一般在别的数据结构不能使用的时候才考虑用前向星。除了不能直接用起点终点定位以外，前向星几乎是完美的。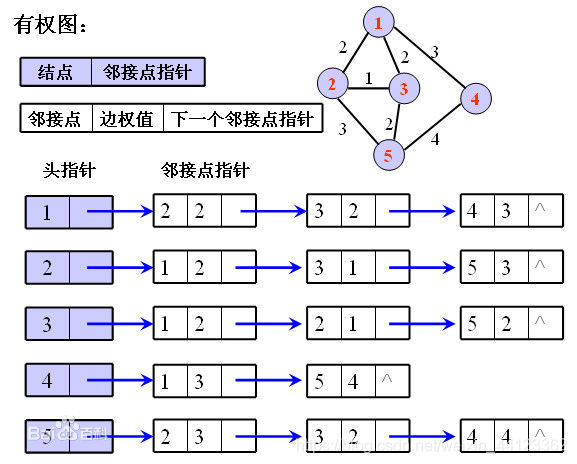
在这里插入图片描述

效率：

时间复杂度O(m)，m为边数，总体时间并不会逊色于邻接表。

代码如下：

其中edge[i].to表示第i条边的终点,edge[i].next表示与第i条边同起点的下一条边的存储位置,edge[i].dis为边权值
另外还有一个数组head[],它是用来表示以i为起点的第一条边存储的位置,实际上你会发现这里的第一条边存储的位置其实在以i为起点的所有边的最后输入的那个编号

#include<iostream>
#include<algorithm>
#include<stdio.h>
#define MAXE 600
#define MAXN 600
using namespace std;

int m,cnt=0,head[MAXN];
//另外还有一个数组head[],它是用来表示以i为起点的第一条边存储的位置,实际上你会发现这里的第一条边存储的位置其实
//在以i为起点的所有边的最后输入的那个编号

struct edge{
    int to;//其中edge[i].to表示第i条边的终点
    int nxt;//edge[i].next表示与第i条边同起点的下一条边的存储位置
    int dis;//edge[i].dis为边权值
}e[MAXE];

void add(int u,int v,int dis){//加边
    e[cnt].dis=dis;
    e[cnt].to=v;
    e[cnt].nxt=head[u];
    head[u]=cnt++;
}

int main(){
    memset(head,-1,sizeof(head));//head[]数组一般初始化为-1
    scanf("%d",&m);
    int a,b,len;
    for(int i=0;i<m;i++){
        scanf("%d%d%d",&a,&b,&len);
        add(a,b,len);
    }
    return 0;
}

我们以这张图为例：

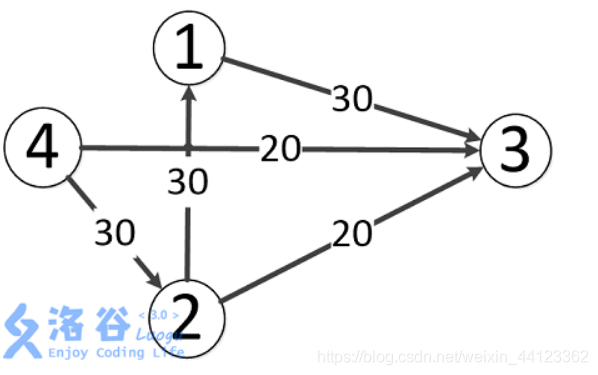
在这里插入图片描述

输出的数据如下：

1 3 30

2 1 30

2 3 20

4 2 30

4 3 20

初始化cnt = 0,这样,现在我们还是按照上面的图和输入来模拟一下:

edge[0].to = 3; edge[0].next = -1; head[1] = 0;

edge[1].to = 1; edge[1].next = -1; head[2] = 1;

edge[2].to = 3; edge[2].next = 1; head[2] = 2;

edge[3].to = 2; edge[3].next = -1; head[4] = 3;

edge[4].to = 3; edge[4].next = 3; head[4] = 4;

很明显,head[i]保存的是以i为起点的所有边中编号最大的那个,而把这个当作顶点i的第一条起始边的位置。这样在遍历时是倒着遍历的,也就是说与输入顺序是相反的,不过这样不影响结果的正确性。
比如以上图为例,以节点2为起点的边有2条,它们的编号分别是1,2 而head[2] = 2，我们在遍历以u节点为起始位置的所有边的时候是这样的:
for(int i = head[u] ; i != -1; i = edge[i].next)
那么就是说先遍历编号为2的边,也就是head[2],然后就是edge[2].next,也就是编号1的边。然后因为edge[1],next==-1，所以就退出了，这样就遍历完成了

来源：CSDN

作者：化身孤岛的鲸o

链接：https://blog.csdn.net/weixin_44123362/article/details/104212039

标签

遍历

数组