96. 不同的二叉搜索树

思路：参考解答
假设n个节点存在二叉排序树的个数是G(n)，令f(i)为以i为根的二叉搜索树的个数，则：
G(n)=f(1)+f(2)+f(3)+f(4)+...+f(n)
当i为根节点时，其左子树节点个数为i-1个，右子树节点为n-i，则：
f(i)=G(i−1)∗G(n−i)
综合两个公式可以得到 卡特兰数 公式：
G(n)=G(0)∗G(n−1)+G(1)∗G(n−2)+...+G(n−1)∗G(0)
递推公式：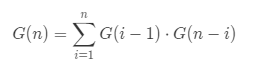

class Solution:
    def numTrees(self, n: int) -> int:
        # f(j)=G(j−1)∗G(i−j)
        # G(i)=f(1)+f(2)+f(3)+f(4)+...+f(i)
        if n<=1:return 1
        G = [0 for _ in range(n+1)]
        G[0],G[1] = 1,1
        for i in range(2,n+1):# 求解G[2]到G[n]
            for j in range(1,i+1): # 叠加求G[i]
                G[i] += G[j-1]*G[i-j]
        return G[n]

来源：CSDN

作者：三岁与十八

链接：https://blog.csdn.net/qq_27921205/article/details/104202088