最短路径问题
最短路径问题的抽象
在网络中,求两个不同顶点之间的所有路径中,边的权值之和最小的那一条路径。
- 这条路径就是两点之间的最短路径
- 第一个顶点为源点
- 第二个顶点为终点
问题分类
- 单源最短路径问题:从某个固定源点出发,求其到所有其他顶点的最短路径: 1. 无权图 2.有权图
- 多源最短路径问题:求任意两顶点间的最短路径
无权单源最短路径算法 --BFS
按照递增的顺序找出到各个顶点的最短路,从而算出到终点的最短路。也可以想象为权值为1的有权单源最短路问题,解决这类问题最好的办法就是上次讲的BFS宽度优先搜索算法去解决。
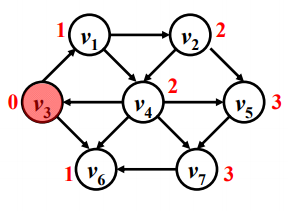
这里以这个图为例,求从v1到v7的最短路径。
#include <iostream>
#include <stdlib.h>
#include <stack>
#include <queue>
#include <string.h>
using namespace std;
int mat[100][100];
int v, e;
int start;
int stop;
void draw()
{
cin >> v >> e;
cin >> start >> stop;
for (int i = 0; i < e; i++)
{
int v1, w1;
cin >> v1 >> w1;
mat[v1][w1] = 1;
}
}
void BFS(int start, int stop)
{
int dis[v+1];
int path[v+1];
memset(path, -1, sizeof(path));
int find = 1;
queue<int> q;
q.push(start);
int Find = 0;
dis[start] = 0 ;
while (!q.empty() && Find == 0)
{
int item = q.front();
q.pop();
for (int i = 1; i <= v; i++)
{
if (mat[item][i] == 1 && path[i] == -1)
{
path[i] = item;
dis[i] = dis[item] + 1 ;
if (i == stop)
{
Find = 1;
break;
}
q.push(i);
}
}
}
if (Find == 0)
{
cout << "Not path!" << endl;
}
else
{
stack<int> s;
cout << "最短路径长度"<<dis[stop]<<" : ";
while (true)
{
s.push(stop);
if (stop == start)
break;
stop = path[stop];
}
while (!s.empty())
{
cout << s.top() << " ";
s.pop();
}
}
}
int main()
{
memset(mat, 0, sizeof(mat));
draw();
BFS(start, stop);
return 0;
}
/*
7 12
1 7
1 2
1 4
2 4
2 5
3 1
3 6
4 3
4 5
4 7
4 6
5 7
7 6
*/
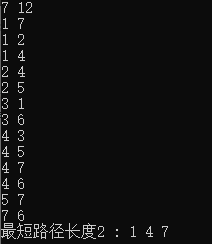
带权单源最短路径算法 --Dijkstra
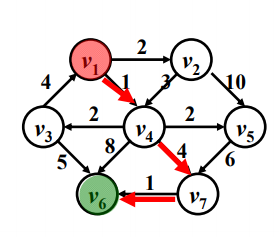
以这幅有向带权图为例,找出从1到6的最短路径。
这个写法是借鉴紫书的,虽然会看起来比较复杂但是效率是很高的,而且可以打印起点到任意点的最短路径。很值得学习!!!!
#include <iostream>
#include <queue>
#include <stdlib.h>
#include <stack>
#include <string.h>
#define maxn 1000
#define INF 1<<30
using namespace std;
struct edge { //定义边结构 储存 起点 终点 权值 可直接 edge(u,v,w)
int from, to, dist;
edge(int u, int v, int w) :from(u), to(v), dist(w) {}
};
struct HeapNode { //优先队列结构 存放 起点到u的最短距离
int d, u;
HeapNode(int d, int u) :d(d) , u(u){}
bool operator < (const HeapNode& rhs) const { //定义 < 符号,用于优先队列排序 最小堆
return d > rhs.d;
}
};
struct Dijkstra { // 将算法封装到结构中,便于使用
int n, m;
vector<edge> edges; //用于储存边 每条边按输入顺序标记 edgs【0】 代表第一条边
vector <int > G[maxn]; // G【i】储存从i点出发的边的序号
bool down[maxn];//判断是否计算过
int dis[maxn];//记录距离
int p[maxn]; // 记录路径
void init(int n)//清空所有数据,初始化结点数n
{
this->n = n;
for (int i = 0; i <= n; i++) G[i].clear();
edges.clear();
memset(p,-1,sizeof (p));
}
void addedges(int u, int v, int w) //插入边
{
edges.push_back(edge(u, v, w));
m = edges.size();
G[u].push_back(m - 1);
}
void dijkstra(int s)// dijkstra算法核心
{
priority_queue<HeapNode> q; //创建一个优先队列
for (int i = 0; i <=n; i++) dis[i] = INF; //将距离初始化为无穷大 1<<30
dis[s] = 0;
q.push(HeapNode(0, s ));//将起点放入队列
memset(down, 0, sizeof(down));
while (!q.empty())
{
HeapNode x = q.top(); q.pop(); //从队列中弹出一个距离最小的结点
int u = x.u;
if (down[u]) continue;
down[u] = true;
for (int j = 0; j < G[u].size(); j++) //更新和这个结点相连的点的最小值,
{
edge& e = edges[G[u][j]];
if (dis[e.to] > dis[u] + e.dist) //注意一点,距离没更新过的话是无穷大的
{
dis[e.to] = dis[u] + e.dist; //距离更小的话 更新距离
p[e.to] = G[u][j]; //记录指向这个点的边 便于后面输出路径
q.push(HeapNode (dis[e.to], e.to ));
}
}
}
}
void printpath(int start,int stop)
{
stack<int> s;
s.push(stop); //寻找到路径是倒着的要用栈去反转下
while (p[stop]!=-1) //只有起点的p值是-1 找到起点后就可以推出循环了
{
stop = edges[p[stop]].from;
s.push(stop);
}
while (!s.empty())
{
cout <<s.top()<<" ";
s.pop();
}
}
};
int main()
{
int n, m;
int start, stop;
Dijkstra d;
cin >> n >> m;
cin >> start >> stop;
d.init(n);
d.m = m;
for (int i = 0; i < m; i++)
{
int u, v, w;
cin >> u >> v >> w;
d.addedges(u, v, w);
}
d.dijkstra(start);
cout << start<<"到"<<stop<<"的最短路径长度:"<<d.dis[stop]<<endl;
d.printpath(start,stop);
return 0;
}
/*
7 12
1 6
1 2 2
1 4 1
2 4 3
2 5 10
3 1 4
3 6 5
4 3 2
4 5 2
4 7 4
4 6 8
5 7 6
7 6 1
*/
注意:迪杰斯特拉算法只适用于权值为正的路径
Dijkstra 衍生问题
-
要求数最短路径有几条
设count[m]计数 条数 -
count[s] = 1 ;起点为1条
-
如果找到更短路: count[w] =count[v]
-
如果找到等长路: count[w] +=count[v] 不是加一
-
要求边数最小的最短路
-
count【s】 = 0 ;
-
如果找到更短路 :count【w】 = count【v】 +1 ;
-
如果找到等长路: count【w】 = count【v】 + 1;
多权最短路算法(Floyd)

同样以这个图为演示示例
#include <iostream>
#include <algorithm>
using namespace std ;
#define INF 1<<25
int main ()
{
int dis[100][100];
fill(dis[0],dis[0]+10000,1<<25);
int n, m ;
cin >> n >> m;
for (int i = 0;i<m;i++)
{
int u,v,w ;
cin >> u>>v>>w ;
dis[u][v]=w ;
}
for (int i=1;i<=n;i++) dis[i][i] = 0;
for (int k=1;k<=n ;k++)
for (int i=1;i<=n;i++)
for (int j=1;j<=n;j++)
dis[i][j] = min(dis[i][j],dis[i][k]+dis[k][j]);
for (int i=1;i<=n;i++)
for (int j=1;j<=n;j++)
{
if (i==j) continue ;
if (dis[i][j] ==1<<25 ) continue ;//无路径
cout <<i<<"->"<<j<<" "<<dis[i][j]<<endl;
}
return 0;
}
/*
7 12
1 2 2
1 4 1
2 4 3
2 5 10
3 1 4
3 6 5
4 3 2
4 5 2
4 7 4
4 6 8
5 7 6
7 6 1
*/

习题:旅游规划
有了一张自驾旅游路线图,你会知道城市间的高速公路长度、以及该公路要收取的过路费。现在需要你写一个程序,帮助前来咨询的游客找一条出发地和目的地之间的最短路径。如果有若干条路径都是最短的,那么需要输出最便宜的一条路径。
输入格式:
输入说明:输入数据的第1行给出4个正整数N、M、S、D,其中N(2≤N≤500)是城市的个数,顺便假设城市的编号为0~(N−1);M是高速公路的条数;S是出发地的城市编号;D是目的地的城市编号。随后的M行中,每行给出一条高速公路的信息,分别是:城市1、城市2、高速公路长度、收费额,中间用空格分开,数字均为整数且不超过500。输入保证解的存在。
输出格式:
在一行里输出路径的长度和收费总额,数字间以空格分隔,输出结尾不能有多余空格。
输入样例:
4 5 0 3
0 1 1 20
1 3 2 30
0 3 4 10
0 2 2 20
2 3 1 20
输出样例:
3 40
这题只需要再更新距离的位置加一个跟新费用的条件,在距离相同但是费用更低的情况下也要更新!
#include <iostream>
#include <stdlib.h>
#include <vector>
#include <queue>
#include <string.h>
#include <algorithm>
#define INF 99999999
#define Max 600
using namespace std ;
struct edge{
int from , to ,dis ,fare ;
edge(int u, int v ,int d ,int f):from(u),to(v),dis(d),fare(f){}
};
struct node{
int dis , n ;
node(int d, int n ):dis(d),n(n) {}
bool operator < (const node& rhs)const{
return dis > rhs.dis;
}
};
struct Dijkstra {
int v ,e ;
vector <edge> edges ;
vector <int> m[Max];
bool down[Max];
int dis[Max];
int far[Max];
void ini(int n)
{
this->v = n;
for (int i=0;i<n;i++)
m[i].clear();
edges.clear();
memset(down,0,sizeof (down));
fill(dis,dis+Max , INF);
fill(far,far+Max , INF);
}
void insertedge(int u ,int v ,int w ,int f)
{
edges.push_back(edge(u,v,w,f));
e = edges.size();
m[u].push_back(e-1);
}
void dijkstra(int start)
{
priority_queue <node> q ;
//ini(v);
dis[start] = 0 ;
q.push(node(0,start));
far[start] = 0;
while (!q.empty())
{
node x = q.top();q.pop();
int u = x.n ;
if (down[u] == true)
continue ;
down[u] = true ;
for(int i=0;i<m[u].size();i++)
{
edge &E = edges[m[u][i]];
if (dis[E.to] >dis[u]+E.dis || (dis[E.to] == dis[u]+E.dis && far[E.to] > far[u] + E.fare))
{
dis[E.to] = dis[u]+E.dis ;
far[E.to] = far[u] + E.fare;
q.push(node(dis[E.to],E.to));
}
}
}
}
};
int main ()
{
int v ,e ,start , stop ;
cin >> v>>e>>start >>stop;
Dijkstra D ;
D.ini(v+1);
for (int i=0 ;i<e;i++)
{
int from ,to ,weight, fare ;
cin >> from >> to >> weight >> fare ;
D.insertedge(from,to,weight,fare);
D.insertedge(to,from,weight,fare);
}
D.dijkstra(start);
cout <<D.dis[stop]<<" "<<D.far[stop]<<endl;
}
这题卡了很久,最后发现是输入上出了问题,模板是有向边,而这题是无向边,所以插入边的地方需要小小的修改!!!!
来源:CSDN
作者:闽院ACMer
链接:https://blog.csdn.net/qq_20225851/article/details/104172850