leetcode11 盛最多的水

利用双指针方法解决本题。。（貌似还可以利用栈来解决，不过思路可能要复杂一些。）

本题抛开具体问题，想到双指针解决是降低时间复杂度的关键一步，本题如果利用暴力法解决，时间复杂度为O(n^2)，

但是采用双指针法解决，时间复杂度会降低到O(n)。

时间复杂度为O(n)，说明问题必须要在遍历一遍数组就解决。

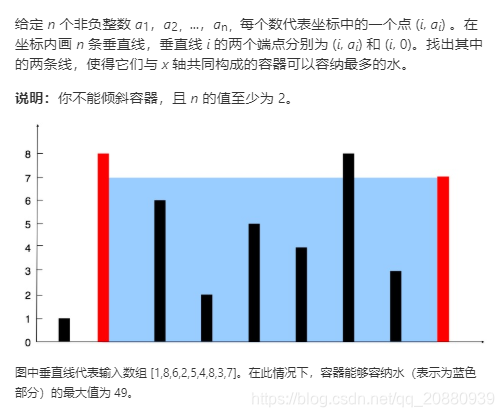
从图上可直观看出，两线段之间形成的区域总是会受到其中较短那条长度的限制。此外，两线段距离越远，得到的面积就越大。

我们在由线段长度构成的数组中使用两个指针，一个放在开始，一个置于末尾。 此外，我们会使用变量 maxarea来持续存储到目前为止所获得的最大面积。 在每一步中，我们会找出指针所指向的两条线段形成的区域，更新 maxarea，并将指向较短线段的指针向较长线段那端移动一步。

class Solution {
public:
    int maxArea(vector<int>& height) {
        int L = 0;
        int R = height.size()-1;
        int max_Area = 0;
        while(L!=R){
            int temp = min(height[L],height[R])*(R-L);
            if(temp>max_Area)
                max_Area = temp;
            if(height[L]<height[R]){
                L++;
            }else{
                R--;
            }
        }
        return max_Area;
    }
};

来源：CSDN

作者：qq_20880939

链接：https://blog.csdn.net/qq_20880939/article/details/104072038