感悟数据结构的实验真的很重要,感觉实验做的好一般都能得高分,所以大家做完正式实验后尽量做一下补充实验有好处。时间和精力有限,我只是整理了正式实验的,好了上干货。
1.实验一 递归练习
1)要求:

(我只是完善逻辑,并没有关于输入输出格式的代码。)
2)逻辑
以四个数为例:全排列数为24,只以一为开头的有6种
1.2.3.4为第一个。
1.2.4.3
1.3.2.4
1.3.4.2
1.4.3.2
1.4.2.3
每当长度等于4时就输出结果,递归地将位置交换
for (int i = start; i < end; ++i) {
swap(list[start],list[i]);
permutation(list,start+1,end);
swap(list[start],list[i]);
}
3)代码:
//输出方法
void system(int list[],int end){
for (int i = 0; i < end ; ++i) {
cout<<list[i];
if(i!=end-1){
cout<<",";
}
}
cout<<endl;
}
//实现方法
void permutation(int list[],int start,int end){
if(start == end){
system(list,end);
} else{
for (int i = start; i < end; ++i) {
swap(list[start],list[i]);
permutation(list,start+1,end);
swap(list[start],list[i]);
}
}
}
结果:
2.排序算法
1)要求:
使用排序方法1-Bubble Sort,2-Insert Sort,3-Radix Sort对 2-20 个不为零的正整数进行排序。
Bubble Sort:
冒泡排序又称为泡式排序,是一种简单的排序算法。它重复地走访过要排序的数列,一次比较两个元素,如果他们的顺序错误就把他们交换过来。走访数列的工作是重复地进行直到没有再需要交换,也就是说该数列已经排序完成。这个算法的名字由来是因为越小的元素会经由交换慢慢“浮”到数列的顶端
Insert Sort:
插入排序是一种简单直观的排序算法。
Radix Sort:
基数排序是一种非比较型整数排序算法,其原理是将整数按位数切割成不同的数字,然后按每个位数分别比较。
2)逻辑
冒泡排序:
1.比较相邻的元素。如果第一个比第二个大,就交换他们两个。
2.对每一对相邻元素作同样的工作,从开始第一对到结尾的最后一对。这步做完后,最后的元素会是最大的数。
3.针对所有的元素重复以上的步骤,除了最后一个。
4.持续每次对越来越少的元素重复上面的步骤,直到没有任何一对数字需要比较。
插入排序:
它的工作原理是通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入。
基数排序:
将所有待比较数值(正整数)统一为同样的数字长度,数字较短的数前面补零。然后,从最低位开始,依次进行一次排序。这样从最低位排序一直到最高位排序完成以后,数列就变成一个有序序列。(利用箱子排序的稳定性!)
3)代码
冒泡排序:
//及时终止的冒泡排序
void bubbleSort(int a[],int n){
bool sorted = false;//用于控制终止程序
for(int i=1;i<n&&!sorted;i++){//控制进行冒泡的次数,冒n-1次
sorted = true;//如果数组没有经过一次交换说明当前数组已经处于有序状态,则无需进行排序了
for(int j=0;j<n-i;j++){
if(a[j+1]<a[j]) {
swap(a[j],a[j+1]);
sorted = false;
}
}
}
}
插入排序:
//插入排序法
void insert(int a[],int n,const int x ){
int i = 0;
for(i=n-1;i>=0&&x<a[i];i--) a[i+1] = a[i];//凡是比x大的就右移一格!!!重要的一点数组的长度必须大于n
a[i+1] = x;
}
void insertSort(int a[],int n){
for(int i=1;i<n;i++){
int t = a[i];
insert(a,i,t);//将右边的元素逐渐插入到左边有序的序列中
}
}
基数排序:
这个比较难理解:参考
//基数排序
bool radixSort(int a[],int n){
for (int i = 0; i < sizeof(a)/ sizeof(int) ; ++i) {
if (a[i]>9){
cout<<"0"<<endl;
return false;
}
}
int box[10][20];//定义二维数组,并赋初值
for (int k = 0; k < 10; ++k) {
for (int i = 0; i < 20; ++i) {
box[k][i] = -1;
}
}
for (int j = 0; j < n; ++j) {
int t = 0;
while (box[a[j]][t] != -1){
t++;//相同基数的数字也能正常排序
}
box[a[j]][t] = a[j];
}
int num = 0;
for (int l = 0; l < 10; ++l) {
for (int i = 0; i < 20 ; ++i) {
if (box[l][i]!=-1){
a[num] = box[l][i];
num++;
} else{
break;
}
}
}
return true;
}
3.线性表的操作
这个比较简单几乎就是书上的代码,这里就不赘述了。
4.堆栈的应用
这个我当时做的非常之艰难,查了好多博文,但是当思路真正弄清楚后一切就豁然开朗了。
1)要求

2)逻辑
我一开始想的是把所有符号全部放入堆栈然后一个一个取出然后计算,但是总是不对,栈(stack)又名堆栈,它是一种运算受限的线性表。限定仅在表尾进行插入和删除操作的线性表。 既然这样那么如果将所有符号全部压入栈在计算就会变得异常困难,不如边压入栈边计算。
我设置两个栈一个放数字,一个放符号
数字的关键在于将多位数压入栈中
符号的关键在于判断优先级和括号的处理
将输入的运算式作为字符串,每个字符依次输入,当其为数字时看前一个是否为数字,是则合为一起压入数字栈,否则直接压入数字栈。当其为符号时,对前面的符号判断优先级,如果前面的高,则将前面的运算结果压入数字栈,然后将符号压入符号栈,否则直接将符号压入符号栈。
3)代码
在思路之外,提前将符号栈压入一个特殊符号,利于判断符号栈是否到头和符号的压入栈。
1.判断字符是否是数字
//判断字符是否为数字
bool isnum(char location) {
int num_lo = location;
if (num_lo>=48&&num_lo<=57){
return true;
}
return false;
}
2.计算数字的运算结果
//用与计算结果的方法,参数是数字堆栈和运算符判断
template <class T>
void result(char ch,linkedStack<T> &figures) //计算并将计算结果压入栈中
{
T x,y,result;
x=figures.top();
figures.pop();
y=figures.top();
figures.pop();
switch(ch)
{
case '+':result=y+x;break;
case '-':result=y-x;break;
case '*':result=y*x;break;
case '/':result=y/x;break;
}
figures.push(result);
}
3.判断符号的优先级
//运算符和前一个运算符的优先级比较
bool prev(char s1,char s2 ){
if(s1=='*'||s1=='/') //如果栈顶符号为* / 则不用考虑输入拿来比较的符号,直接返回真
return true;
else if((s1=='+'||s1=='-')&&(s2=='+'||s2=='-'))//如果栈顶符号和拿来比较的符号为+或者-,也返回真
return true;
else
return false; //其他情况都返回假
}
4.主运算函数
int calculate(string str){
char *ch = (char*)str.c_str();//可以将string赋给char*
linkedStack<char> symbols;//存运算符
linkedStack<int> figures;//存整数,只舍不入
symbols.push('O');//添加一个结束(开始)的标记位,省去很多判断的麻烦
char previous;//用于记录栈顶运算符
for (int i = 0; i <str.size() ; ++i) {
char temp = ch[i];
int figure = 0;
if (isnum(temp)){
if (i==0){//如果第一个字符是数字则无序判断前面是否也是数字
figure = (temp-'0');//char->int
figures.push(figure);
} else{
if (isnum(ch[i-1])){
figures.top() = figures.top()*10+(temp-'0');
} else{//前面不是数字则将自己压入栈中
figure = (temp-'0');
figures.push(figure);
}
}
} else if (temp=='('){
symbols.push(temp);
} else if (temp==')'){//右括号不如符号栈
previous = symbols.top();
while (previous!='('){
result(previous,figures);
symbols.pop();
previous = symbols.top();
}
symbols.pop();//将( 弹出栈
}
//是运算符
else{
previous = symbols.top();
while (prev(previous,temp)){
result(previous,figures);
symbols.pop();//将已经运算过的运算符弹出栈
previous = symbols.top();//再比较更前面的
}
symbols.push(temp);//将未运算的符号压入栈中
}
}
previous = symbols.top();
while (previous!='O'){//只要还有运算符计算就没结束
result(previous,figures);
symbols.pop();
previous=symbols.top();
}
return figures.top();
}
栈的数据结构实现形式可以是数组可以是链表,个人倾向于链表。将头结点作为栈顶十分便捷,插入和删除操作都集中在头结点。
插入:
void push(const T& theElement){//压栈时无需判断栈是否为空
stackTop = new chainNode<T>(theElement,stackTop);//很巧妙!
stackSize++;
}
删除:
void pop(){
if (stackSize == 0) throw;
//stackTop = stackTop->next;错误删除方法,只是改变头结点位置并没有真正删除第一个元素。
chainNode<T> *temp = stackTop->next;
delete stackTop;
stackTop = temp;
stackSize--;
}
5.二叉树操作
1)要求
二叉树(英语:Binary tree)是每个节点最多只有两个分支(即不存在分支度大于2的节点)的树结构。通常分支被称作“左子树”或“右子树”。二叉树的分支具有左右次序,不能随意颠倒。
二叉树是本课程最为重要的部分之一,可考的很多,遍历,节点数目,高度,叶子节点的数目……
1、输入一个完全二叉树的层次遍历字符串,创建这个二叉树,输出这个 二叉树的前序遍历字符串、中序遍历字符串、后序遍历字符串、结点 数目、二叉树高度(上述每一个结果独立一行显示)。
2、输入二叉树前序序列和中序序列(各元素各不相同),创建这个二叉 树,输出该二叉树的后序序列、层次遍历。
2)逻辑
1、由完全二叉树的层次遍历创建二叉树比较简单。利用队列将元素逐渐放到完全二叉树上。
2、由前序和中序序列创建二叉树,比较难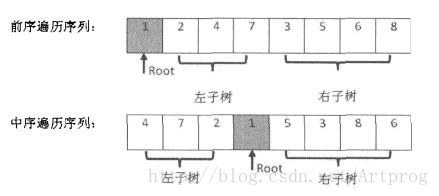
根据前序判断根节点,根据中序和根节点的位置确定左右子树一直这样逐渐形成一棵树。
3)代码
1.由层次遍历创建完全二叉树
template<class T>
//按层次遍历的顺序创建树
void linkedBinaryTree<T>::LevelCreateTree(int nodeSize,char* string) {
treeSize = nodeSize;
//层次遍历有关的都要结合队列来做
arrayQueue<binaryTreeNode<T>*> *queues = new arrayQueue<binaryTreeNode<T>*>;
int count = 1;
binaryTreeNode<T> *node = new binaryTreeNode<T>();//用来移动的节点Node
root = new binaryTreeNode<T>();
node = root;
root->element = string[count-1];//头结点
//只有一个元素时
if (count == nodeSize){
return;
}
queues->push(node);//将头节点放入队列中
while (!queues->empty()) {
node = queues->front();
queues->pop();
if (node->leftChild == NULL) {
binaryTreeNode<T> *left = new binaryTreeNode<T>();
left->element = string[count];
node->leftChild = left;
queues->push(left);
count++;
if (count == nodeSize)//这时候中止并不会有数组越界的bug
break;
}
if (node->rightChild == NULL) {
binaryTreeNode<T> *right = new binaryTreeNode<T>;
right->element = string[count];
node->rightChild = right;
queues->push(right);
count++;
if (count == nodeSize)
break;
}
}
}
2.树的高度
template <class T>
//计算树的高度
int linkedBinaryTree<T>::height_tree(binaryTreeNode<T>* tree){
if(tree==NULL) return 0;
else return 1+max(height_tree(tree->leftChild),height_tree(tree->rightChild));//!!!!不要忘记1是父节点
}
3.树的节点数目
template <class T>
//计算树的结点个数
int linkedBinaryTree<T>::getNodesNum(binaryTreeNode<T> *root) {
if (root==NULL) return 0;
else return 1+getNodesNum(root->leftChild)+getNodesNum(root->rightChild);
}
4.由前序和中序遍历创建二叉树
//利用前序遍历和中序遍历创建二叉树
template <class T>
binaryTreeNode<T>* linkedBinaryTree<T>::CreateByPreIn(T *VLR, T *LVR, int n) {//n是前序或者中序结果的长度
if (n == 0)
return NULL;
int k = 0;
while (VLR[0] != LVR[k])
k++;
binaryTreeNode<T> *t = new binaryTreeNode<T>();
t->element = VLR[0];//父节点创建
t->leftChild = CreateByPreIn(VLR + 1, LVR, k);
t->rightChild = CreateByPreIn(VLR + k + 1, LVR + k + 1, n - k - 1);
return t;
}
6.堆和搜索树
1)要求
1、输入一系列不为零的正整数(最多不超过 20 个),遇到 0 代表输入 结束(不包含 0)。
2、根据上面输入的数据序列,用初始化方法创建最大堆(不要用节点依 次插入的办法创建最大堆),然后输出最大堆的层次序列。
3、输出用堆排序后的排序结果。
4、根据上面输入的数据,创建二叉搜索树(关键字不允许重复,如遇重 复,则不重复插入该关键字),输出二叉搜索树的前序序列、中序序 列(分行输出)。
二叉查找树(英语:Binary Search Tree),也称为二叉搜索树、有序二叉树(ordered binary tree)或排序二叉树(sorted binary tree),是指一棵空树或者具有下列性质的二叉树:
1.若任意节点的左子树不空,则左子树上所有节点的值均小于它的根节点的值;
2.若任意节点的右子树不空,则右子树上所有节点的值均大于它的根节点的值;
3.任意节点的左、右子树也分别为二叉查找树;
4.没有键值相等的节点。
2)逻辑
1.堆的初始化:
最大堆一定为完全二叉树所以用数组表示最为方便。
以最小堆的初始化为例
为了将图一的完全二叉树转变为最小堆,从最后一个具有孩子的节点(97)开始将孩子中最小的与自己比较,如果比孩子大则交换(如果以这个节点为根的节点不是最小堆则将其转换为最小堆。)一直转换到根。
2.堆排序
将堆初始化然后依次删除根节点即可得到有序的数列。
3.二叉搜索树
将元素依次插入到二叉搜索树中:
3)代码
1.堆的初始化:
//堆的初始化,时间复杂度为Θ(n),比一个一个的插入性能要好一些
template <class T>
void maxHeap<T>::initialize(T *theHeap, int theSize) {
delete [] heap;
heap = theHeap;
heapSize = theSize;
//从第一个有孩子的节点开始排查
for (int root = heapSize/2; root >=1 ; --root) {
T theElement = heap[root];
int child = 2*root;
while (child<=heapSize){
if (child<heapSize&&heap[child]<heap[child+1]){
child++;//获取大孩子
}
if (theElement>=heap[child]){
break;
}
//父子交换
heap[child/2] = heap[child];
child *= 2;
}
heap[child/2] = theElement;
}
}
2.堆排序:
template <class T>
T* sort2(T a[],int n){
maxHeap<T> heap(1);
heap.initialize(a,n);
for (int i = n-1; i >=1 ; --i) {
T x = heap.top();
heap.pop();
a[i+1] = x;
}
return a;
}
3.二叉树的插入:
template <class K>
void binarySearchTree<K>::insert(int & thePair) {
// cout<<thePair<<endl;检验代码
binaryTreeNode<int> *pp = NULL;
binaryTreeNode<int> *p = this->root;//问题:c++模板类在继承中子类无法访问父类的成员 解决方法:在子类访问父类时加上父类的前缀或使用this->调用
while (p!=NULL){
pp = p;//记录p的位置
if(thePair<p->element){//要插入的元素比当前元素小,往左子树走
p = p->leftChild;
} else{
if (thePair>p->element){
p = p->rightChild;
} else{
return;//不重复插入元素,并不覆盖
}
}
}
binaryTreeNode<int> *newNode = new binaryTreeNode<int>(thePair);
if (this->root!=NULL){
if (pp->element>thePair){
pp->leftChild = newNode;
} else{//不存在=的情况
pp->rightChild = newNode;
}
} else{
this->root = newNode;
}
this->treeSize++;
}
7.图的操作
1)要求
1.输出从第 1 节点到第 n 节点最短路径的长度,如果没有路经,输出 0。(单源最短路径)
2.输出最小生成树的所有边。
2)逻辑
1.使用迪杰斯特拉算法
2.使用最小生成树算法
迪杰斯特拉:(伪码)(提示考试让你写代码,如果真的写不出C++代码建议写伪码)


最小生成树算法
有三种算法:
Kruskal算法,Prim算法,Sollin算法。(重点掌握前两种)
1.Kruskal算法
从剩下的边集中选出一条成本最小的且不会与已加入的边产生环路
难点如何判读加入边后不会产生环路,使用等价类。
2.Prim算法
从剩余的边中选出一条成本最小的边并能加入已选入的边集中形成树。

3)代码:
迪杰斯特拉算法:
//3.迪杰斯特拉算法
void Dijkstra(int n, int v){
int maxnum = 100;
int **c = a;
int dist[n+1];
int prev[n+1];
bool s[maxnum]; // 判断是否已存入该点到S集合中
for(int i=1; i<=n; ++i)
{
dist[i] = c[v][i];
s[i] = 0; // 初始都未用过该点
if(dist[i] == noEdge)
prev[i] = 0;
else
prev[i] = v;
}
dist[v] = 0;
s[v] = 1;
// 依次将未放入S集合的结点中,取dist[]最小值的结点,放入结合S中
// 一旦S包含了所有V中顶点,dist就记录了从源点到所有其他顶点之间的最短路径长度
// 注意是从第二个节点开始,第一个为源点
for(int i=2; i<=n; ++i){
int tmp = noEdge;
int u = v;
// 找出当前未使用的点j的dist[j]最小值
for(int j=1; j<=n; ++j)
if((!s[j]) && dist[j]<tmp)
{
u = j; // u保存当前邻接点中距离最小的点的号码
tmp = dist[j];
}
s[u] = 1; // 表示u点已存入S集合中
// 更新dist
for(int j=1; j<=n; ++j)
if((!s[j]) && c[u][j]<noEdge)
{
int newdist = dist[u] + c[u][j];
if(newdist < dist[j])
{
dist[j] = newdist;
prev[j] = u;
}
}
}
if (dist[n]==noEdge){
cout<<0;
} else{
cout<<dist[n];
}
}
Kruskal算法
返回值是bool主要是如果没有生成树则返回false
//4.Ktuskal算法 计算最小生成树
bool kruskal(Edges spanning[]){
int n = this->n;
int e = this->e;
//边集合E
Edges edges[e];
//对边集合E初始化
int k = 0;
for (int i = 1; i <= n ; ++i) {
for (int j = 1; j <= n ; ++j) {
if(existsEdge(i,j)&&i<j){
edges[k].start = i;
edges[k].end = j;
edges[k].weight = a[i][j];
k++;
}
}
}
//并查集问题!
fastUnionFind uf(n+1);
k =0;
while (e>0&&k<n-1){
Edges x = min_from(edges,this->numberOfEdges());
e--;
int a = x.start;
int b = x.end;
if(uf.find(a) != uf.find(b)){//!!!!!!!!!!!!!!!!!!!判断新加入的边是否成环
//加入生成树中
spanning[k++] = x;
uf.unite(a,b);
}
}
return (k == n-1);
}
并查集:也是这门课贯穿始终的问题很重要,也很常用参考博文
class fastUnionFind{
private:
int n;//节点数目
int *node; //每个节点
int *rank; //树的高度
public:
//初始化n个节点
void Init(int n){
for(int i = 0; i < n; i++){
node[i] = i;
rank[i] = 0;
}
}
//构造函数
fastUnionFind(int n) : n(n) {
node = new int[n];
rank = new int[n];
Init(n);
}
//析构函数
~fastUnionFind(){
delete [] node;
delete [] rank;
}
//查找当前元素所在树的根节点(代表元素)
int find(int x){
if(x == node[x])
return x;
return node[x] = find(node[x]); //在第一次查找时,将节点直连到根节点
}
//合并元素x, y所处的集合
void unite(int x, int y){
//查找到x,y的根节点
x = find(x);
y = find(y);
if(x == y)
return ;
//判断两棵树的高度,然后在决定谁为子树
if(rank[x] < rank[y]){
node[x] = y;
}else{
node[y] = x;
if(rank[x] == rank[y]) rank[x]++;
}
}
//判断x,y是属于同一个集合
bool same(int x, int y){
return find(x) == find(y);
}
};
Prim算法
//最小生成树的prim算法
bool Prim(Edges spanning[]){
int n = this->n;
int e = this->e;
//边集合E
Edges edges[e];
//对边集合E初始化
int k = 0;
for (int i = 1; i <= n ; ++i) {
for (int j = 1; j <= n ; ++j) {
if(existsEdge(i,j)&&i<j){
edges[k].start = i;
edges[k].end = j;
edges[k].weight = a[i][j];
k++;
}
}
}
/*
* 链表储存已经加入到TV中的点
*/
chain<int> theVs;
k =0;
theVs.insert(0,1);//起始点是1
while (e>0&&k<n-1){
Edges x = min_from_vs(theVs,edges,this->numberOfEdges());
e--;
spanning[k++] = x;
/*
* 将另一个顶点加入到点集中
*/
if (theVs.indexOf(x.start)==0){
theVs.insert(0,x.start);
} else{
theVs.insert(0,x.end);
}
}
return (k == n-1);
}
关键是判断最小的边加入后是否还是一棵树:
/*
* prim的辅助方法
*/
Edges min_from_vs(chain<int> vs,Edges es[],int bianshu){
Edges temp = es[0];
int index = 0;
int sum = 0;
while(true){
for (int i = 1; i < bianshu-sum ; ++i) {
if (es[i].weight<temp.weight){
temp = es[i];
index = i;
}
}
/*
* 一个顶点在vs中一个顶点不在vs中
*/
if ((vs.indexOf(temp.start)!=0&&vs.indexOf(temp.end)==0)||(vs.indexOf(temp.end)!=0&&vs.indexOf(temp.start)==0)){
es[index].weight = 10000;//相当于删除最小的边
return temp;
} else{
swap(es[index],es[e-1-sum]);
sum++;
}
}
}
好了实验全部写完,希望SDU们在学习的同时能够多敲代码,多看别人的博客,写好实验,这样这门课程一般会是一个不错的成绩。
来源:https://www.cnblogs.com/fxk2020/p/12257369.html