codeforces 1295E 线段树维护

codeforces 1295E 线段树

题目描述：

题面链接：http://codeforces.com/contest/1295/problem/E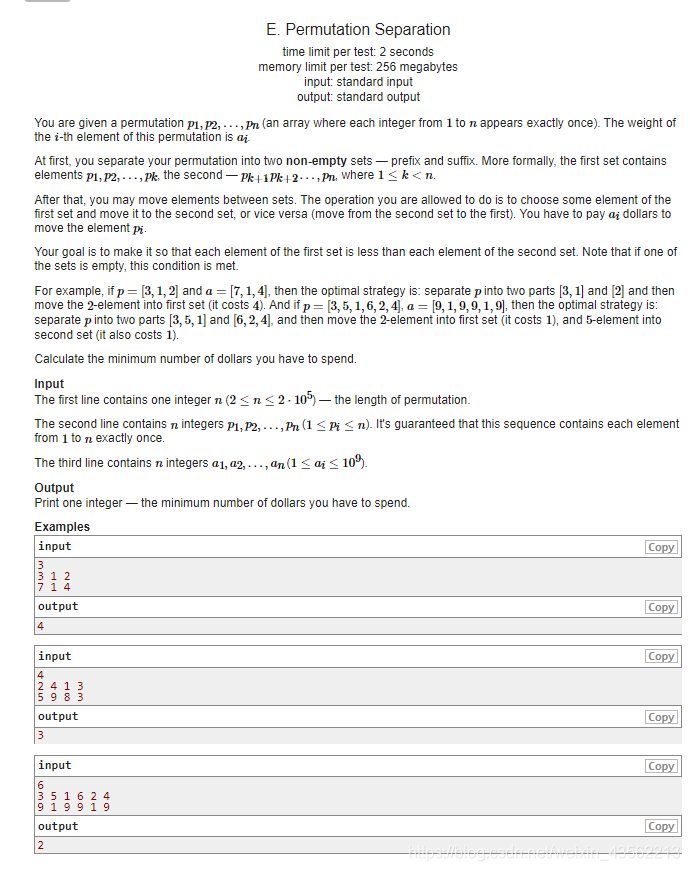

给两个数组p和a，将p数组分割成两部分，然后可以将前部分移动到后部分，反之也可，移动一个数p[i]为对应数的a[i]，问最少花费多少使前部分的值都小于后部分。

解题思路

线段树维护最后前部分的数为0到i的花费的最小值，先初始化将所有数都分到后部分，然后再依次维护分割点为p[1]到p[n-1]所对应的花费最小值，详细看代码。

代码

#include<cmath>
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
typedef long long ll;
ll n;
ll tr[200005*4],tag[200005*4],p[200005],a[200005];
void pushd(ll i){
    tr[i*2]+=tag[i];
    tr[i*2+1]+=tag[i];
    tag[i*2]+=tag[i];
    tag[i*2+1]+=tag[i];
    tag[i]=0;
}
void update(ll i){
    tr[i]=min(tr[i*2],tr[i*2+1]);
}
void meter(ll i,ll L,ll R,ll l,ll r,ll v){
    //cout<<i<<' '<<L<<' '<<R<<' '<<l<<' '<<r<<' '<<v<<endl;
    if(l<=L&&r>=R) {
        tr[i]+=v,tag[i]+=v;return ;
    }
    pushd(i);
    if(r>((L+R)/2)) meter(i*2+1,(L+R)/2+1,R,l,r,v);
    if(l<=((R+L)/2)) meter(i*2,L,(L+R)/2,l,r,v);
    update(i);
}
int main(){
    scanf("%lld",&n);
    for(int i=1;i<=n;i++) scanf("%lld",&p[i]);
    for(int i=1;i<=n;i++){
        scanf("%lld",&a[i]);
        meter(1,0,n,p[i],n,a[i]);//初始化将所有的值都放到后部分
    }
    ll ans=1e18;
    for(int i=1;i<n;i++){
        meter(1,0,n,p[i],n,-a[i]);//将p[i]放回前部分，分割点后移
        meter(1,0,n,0,p[i]-1,a[i]);//由于p[i]此时在前部分，所以所有最后前部分结果为0到k(k<n)的花费要加上将p[i]放到后部分。
      //  cout<<tr[1]<<endl;
        ans=min(ans,tr[1]);
    }
    printf("%lld\n",ans);
}

来源：CSDN

作者：HRBU_Bigspot

链接：https://blog.csdn.net/weixin_43562213/article/details/104117708