一、冒泡排序和插入排序(简单的排序)
冒泡排序原理:依次比较相邻的两个数,将更大的数移到右侧,这样进行一轮,被移到最右边的数肯定是这组数字里最大的。再进行一轮,倒数第二位置放的一定是第二大的数字...以此类推。
时间复杂度分析:顺序 T=O(n) 逆序

JAVA语言:
public static void bubbleSort(int[] arr){
//一定要记住判断边界条件
if(arr==null||arr.length<2){
return;
}
//需要进行arr.length趟比较
for(int i = 0 ;i<arr.length-1;i++){
//第i趟比较
for(int j = 0 ;j<arr.length-i-1;j++){
//开始进行比较,如果arr[j]比arr[j+1]的值大,那就交换位置
if(arr[j]>arr[j+1]){
int temp=arr[j];
arr[j]=arr[j+1];
arr[j+1]=temp;
}
}
}
}
插入排序:每一步将一个待排序的数据插入到前面已经排好序的有序序列中,直到插完所有元素为止。
时间复杂度:平均情况:N^2/4 次比较,N^2/4次交换;
最坏情况:N^2/2次比较,N^2/2次交换;
最好情况:N-1次比较,0次交换;
平均时间复杂度: O(N^2)
最好时间复杂度: O(N)
JAVA代码实现:
public class InsertionSorted extends AbstractSorted {
public <T extends Comparable<T>> void sort(T[] arrays) {
// 开始一趟有序列扫描,当前i之前的数据视为有序序列
for (int i = 1; i < arrays.length; i ++) {
// 寻找位置,从后向前与i之前的有序序列一一比较,找到比当前元素小的位置
for (int j = i; j >= 0 && less(arrays[j], arrays[j - 1]; j --)) {
exch(arrays, j, j - 1);
}
String msg = String.format("第%2d次 ->: %s", i, Arrays.toString(arrays));
System.out.println(msg);
}
}
}
二、希尔排序(shell sort)
希尔排序有时也被叫做缩减增量排序,有一个增量序列来逐步排序。例如下面的例子,先进行间隔5排序,即81、35、41三个数。然后进行3排序,最后进行1排序,逐步地完成排序。
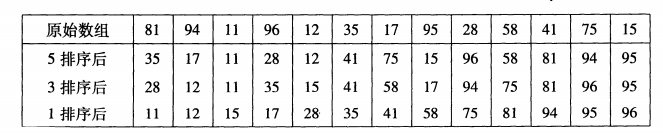
JAVA代码实现:
public static void Shellsort(int [] a){
for(int gap = a.length /2;gap > 0;gap /= 2){
//这里gap指的就是增量序列,这里选择的是不断除以2,这样增量序列其实并不好
for(int i=gap;i<a.length;i++){
int tmp = a[i];//新建一个临时变量用于交换
for(int j=i;j >= gap && tmp.compareTo(a[j-gap]);j-=gap){
//将间隔gap两个元素比较
a[j] = a[j-gap]; //交换
}
a[j] = tmp; //不调换
}
}
}
使用希尔排序依赖于增量序列的选择,最坏的时间复杂度也是

Hibbard增量:1、3、7...
 ,这样最坏时间复杂度
,这样最坏时间复杂度
Sedgewick增量:
 或者
或者 这样最坏的时间复杂度是
这样最坏的时间复杂度是
三、堆排序
在堆排序前,先来看选择排序
算法思想:选择排序,从头至尾扫描序列,找出最小的一个元素,和第一个元素交换,接着从剩下的元素中继续这种选择和交换方式,最终得到一个有序序列。
举个例子方便理解:

JAVA实现:
public static void selectSort(int [] arr,int n){
for (int i = 0; i < n - 1; i++) {
int index = i;
int j;
// 找出最小值得元素下标
for (j = i + 1; j < n; j++) {
if (arr[j] < arr[index]) {
index = j;
}
}
int tmp = arr[index];
arr[index] = arr[i];
arr[i] = tmp;
System.out.println(Arrays.toString(arr));
}
}
堆排序:
堆本身就有最小堆和最大堆,所以这里就直说最小堆。用DeleteMin()弹出最小元素,赋值给有序序列中第一个元素,再在无序序列里弹出最小元素,赋值给有序序列中第二个元素,依次类推。
时间复杂度 T(N) = O(NlogN),但需要O(N)的空间。
JAVA实现:
public void Heapsort(int [] a){
int [] arr = Arrays.copyOf(a,a.length);
int len = a.length;
buildMaxHeap(arr,len);
for(int i = len - 1;i>0;i--){
swap(arr,0,i);
len--;
heapify(arr,0,len);
}
}
private void buildMaxHeap(int[] arr,int len){//创建一个最大堆
for(int i = (int)Math.floor(len/2);i>=0;i--){
heapify(arr,i,len);
}
}
private void heapify(int[] arr,int i,int len){//堆化,就是乱序堆变成最大堆
int left = 2*i+1;
int right = 2*i+2;
int largest = i;
if(left <len && arr[left] > arr[largest]){
largest = left;
}
if(right <len && arr[right] > arr[largest]){
largest = right;
}
if(largest != i){
swap(arr,largest,i);
heapify(arr,largest,len);
}
}
private void swap(int[] arr,int i,int j ){//用于交换的方法
int tmp = arr[i];
arr[i] = arr[j];
arr[j] = tmp;
}
四、归并排序
归并排序基本排序原理:典型的基于分治的递归算法。它不断地将原数组分成大小相等的两个子数组,最终当划分的子数组大小为1时,将划分的有序子数组合并成一个更大的有序数组。先把两个子数组排成有序后,再将其合并成一个有序序列。
JAVA实现:
public void Mergesort(int [] a,int [] tmp,int left,int right){
if(left < right){
int center = (left+right)/2;
Mergesort(a,tmp,left,center);
Mergesort(a,tmp,center+1,right);
merge(a,tmp,0,center+1,right);
}
}
private void merge (int[] a,int[] tmp,int leftPos,int rightPos,int rightEnd){//创建一个最大堆
int leftEnd = rightPos - 1;
int temPos =leftPos;
int numElements = rightEnd - leftPos + 1;
while (leftPos<=leftEnd && rightPos<=rightEnd){
if(a[leftPos].compareTo(a[rightPos]) <= 0){
tmp[temPos++] = a[leftPos];
}else {
tmp[temPos++] = a[rightPos];
}
}
while (leftPos<=leftEnd){
tmp[temPos++] = a[leftPos];
}
while (rightPos<=rightEnd){
tmp[temPos++] = a[rightPos];
}
//tmp数组就已经按从小到大排序好了
}
五、快速排序(面试重点)
快速排序的基本思想原理:
1、先从数列中取出一个数作为基准数
2、分区过程,将比这个数大的数全放到它的右边,小于或等于它的数全放到它的左边
3、再对左右区间重复第二步,直到各区间只有一个数
这里选取的主元也就是基准数的大小就很关键,会直接影响到时间复杂度,一般选取方法是:使用左端、右端、和中心位置上的三个元素的中值作为主元。
举个例子,这里的例子就用书上的例子了:

之后依次对6左边和右边两堆数字再次递归调用快速排序算法。
JAVA实现:
public void quicksort(int [] a,int left,int right){
if(left < right){
int pivot = median3(a,left,right);//设置中值为主元
int i = left, j = right -1;
while(true){
while (a[++i].compareTo(pivot) < 0){}
while (a[--j].compareTo(pivot) > 0){}
if(i < j){
swap(a,i,j);
}else {
break;
}
}
swap(a,i,right-1);//排序完将放在末位置的主元换到应该在的位置
quicksort(a,left,i-1);//将小于主元的一堆数同样递归调用这个方法
quicksort(a,i+1,right);//将大于主元的一堆数同样递归调用这个方法
}
}
private int median3(int [] a,int left,int right){
int center = (left + right) / 2;
if(a[center].compareTo(a[left]) < 0){
swap(a,center,left);
}
if(a[right].compareTo(a[left]) < 0){
swap(a,right,left);
}
if(a[right].compareTo(a[center]) < 0){
swap(a,center,right);
}
swap(a,center,right-1);//将中值放到right-1的位置上
return a[right-1];
}
private void swap(int[] arr,int i,int j ){//用于交换的方法
int tmp = arr[i];
arr[i] = arr[j];
arr[j] = tmp;
}
这里有一种情况:如果元素正好等于pivot怎么办?
我们选择停下来交换这两个元素
tips:当需要排序的数据规模充分小的时候,直接使用插入排序更快;可以使用一个if语句进行判定一下数据规模。
六、基数排序
1.桶排序
基数排序建立在桶排序的基础上,先说说桶排序。
假设我们有N个学生,他们的成绩是0到100之间的整数,如何在线性时间内将学生按成绩排序?
我们准备0到100,共101个桶
将学生成绩对应的放入桶中,然后依照桶的顺序将学生成绩依次输出。
2.基数排序
但是,如果我们有10个整数,每个整数值在0到999之间(M),M>>N,我们不可能去建立1000个桶来放置这10个数。
那我们怎么做呢?
只建立10个桶,0,1,2,3...9
分别按照个位,十位,百位的数字分别插入桶中进行排序。

JAVA实现:
public class BasicSort {
public static void basicSort(int[] array) {
//创建叠加数组
List<ArrayList> dyadic = new ArrayList<>();
//给大数组dyadic添加子数组
for(int i = 0; i < 10; i++) {
ArrayList<Integer> arr = new ArrayList<>();
dyadic.add(arr);
}
//找出数组中的最大值
int max = 0;
for(int i = 0; i <array.length; i++) {
if(array[i] > max) {
max = array[i];
}
}
//判断最大值为几位数,其位数就是应该循环的次数
int times = 0;
while(max > 0) {
max /= 10;
times++;
}
//循环times次,每次将对应位的数分配到相应的自数组中
for(int i = 0; i < times; i++) {
for(int j = 0; j < array.length; j++) {
//找出每个数对应的位的数值
int x = array[j] % (int)Math.pow(10, i + 1) / (int)Math.pow(10, i);
//将该数组作为下标,找到对应的子数组
ArrayList arr = dyadic.get(x);
//将该元素添加到子数组中
arr.add(array[j]);
//因为子数组改变,因此更新大数组
dyadic.set(x, arr);
}
//将重新排好的子数组的值依次将需要被排序的数组的值覆盖
int index = 0; //用index作为数组array的下标
//将子数组依次遍历,将每个子数组中的元素添加到array中
for(int k = 0; k < 10; k++) {
//当下标为k的子数组中有元素时
while(dyadic.get(k).size() > 0) {
//得到该数组
ArrayList arr = dyadic.get(k);
///将该数组的第一个元素添加到array中
array[index] = (int)arr.get(0);
//移除子数组中的第一个元素,这样就能在第一个元素被使用之后,后面元素替换
arr.remove(0);
//将array数组中下标也后移一位
index++;
}
}
}
}
七、排序算法比较
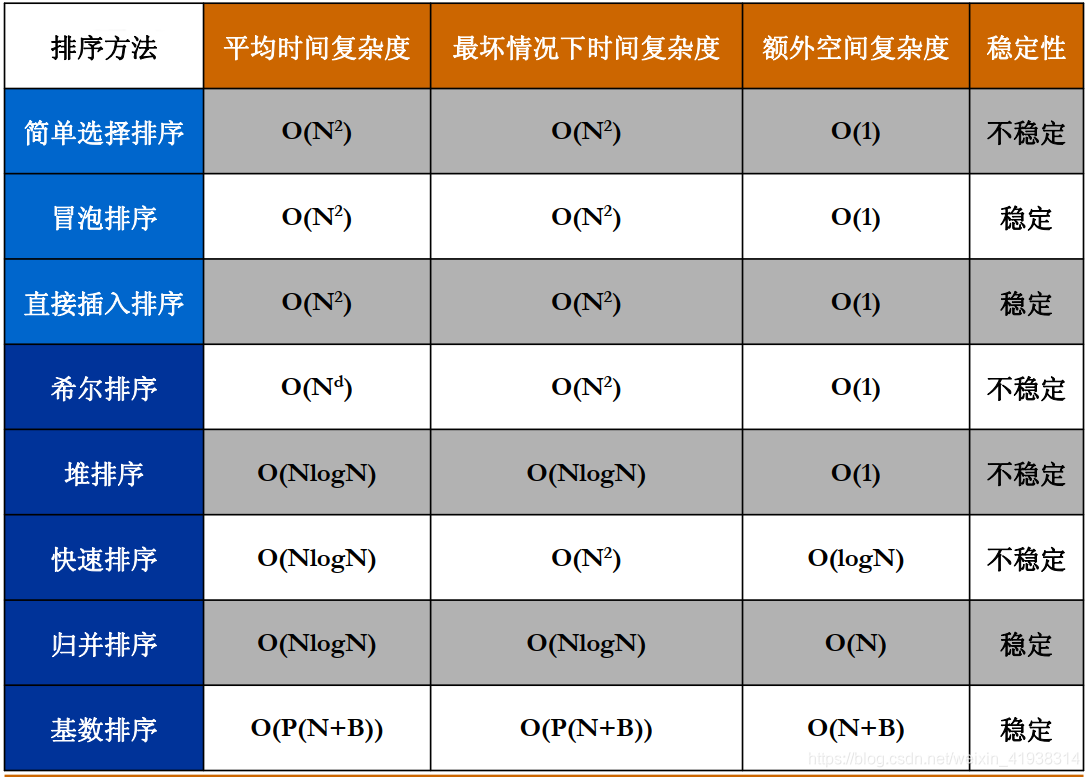
来源:CSDN
作者:半城抹茶
链接:https://blog.csdn.net/weixin_41938314/article/details/104094707