最优二叉搜索树是建立在搜索树的基础上的一种最优解,一开始我也很纠结为什么会有查找不成功和查找成功的概念,后来才开始明白后来懂了如何去做,如果这点还没有明白那很难去懂什么是最优二叉搜索树,下面按照题目讲解主要内容:
我们先来声明一下如何求二叉搜索树的权重
形状1的平均查找次数
形状2的平均查找次数
计算的方程
知道了如何计算平均查找次数,我们下面求解一下如何求解最优二叉搜索树问题
将四个合起来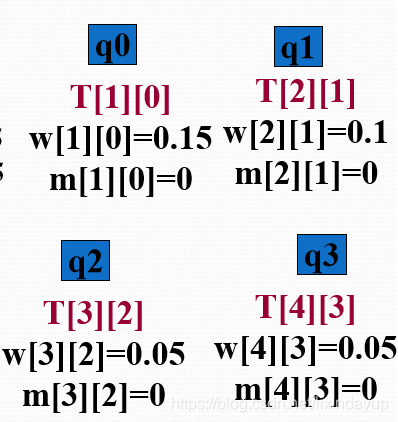
拼成一个个基本的子树暂时命名为a1,a2,a3
a1和a2合并有两种情况
计算得出第一种权重较小,故选择第一种形状为T[1][2]
同理计算出T[2][3]应该为第一种模型
这是最终有a1和a2以及a2和a3形成的最小二叉搜索树的子树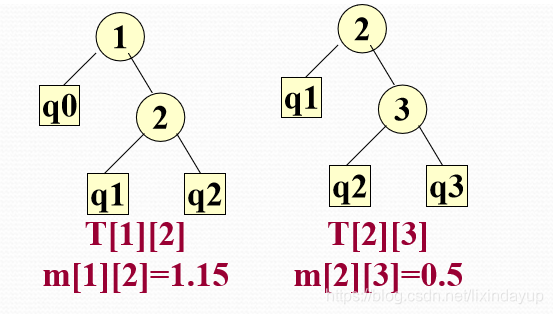
当我们求解T[1][3]时,实际上我们求解的是由T[1][2]与a3构成的,以及a1与T[2][3]构成的其中找到最优解
得出最优解由形状一取得
这是动态规划的动态矩阵以及状态转移方程
来源:CSDN
作者:李小白努力努力努力ing
链接:https://blog.csdn.net/lixindayup/article/details/104098907