软件工程网络15结对编程作业

一、结对编程

• 陈凯欣：学号 201521123034+邱晓娴：学号 201521123037
• 码云地址：https://gitee.com/carolfantasy/software_engineering__pair_programming.git

二、需求分析

1、原项目分析

1.1项目类图

1.2存在的不足

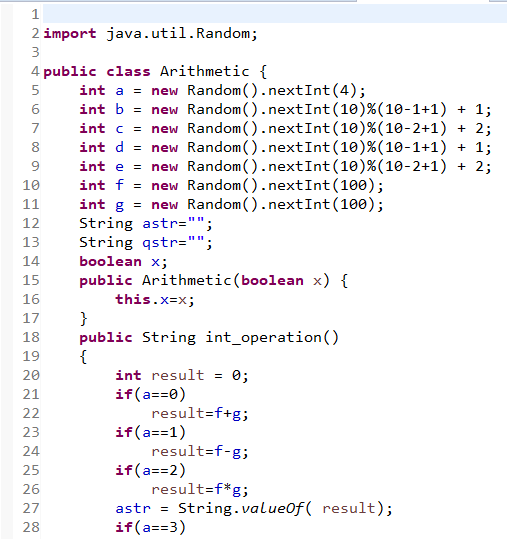
• 变量的命名使用abc，不够规范。a既然表示操作符可以改名为oprator。

• 运行该程序，初次选择计算题数并进行计算，程序会将错题存在错题集中。之后所有的计算练习是在错题集中抽取。需要重新运行该程序才能选择新的题目进行练习。
• 复习错题选择的题数若超过错题集题数，未提示错误。
• 在做题界面中点击开始后修改计时时间，计时器停止运行，最后做题显示时间为手动修改的时间。
• 在做题界面点击开始后，再次点击开始，计时器重新计时。
• 错题集的题目根据每次做题的情况依次累加。若某题错误率高，随机选题复习的话很有可能选的题目都是该题，显得累赘。

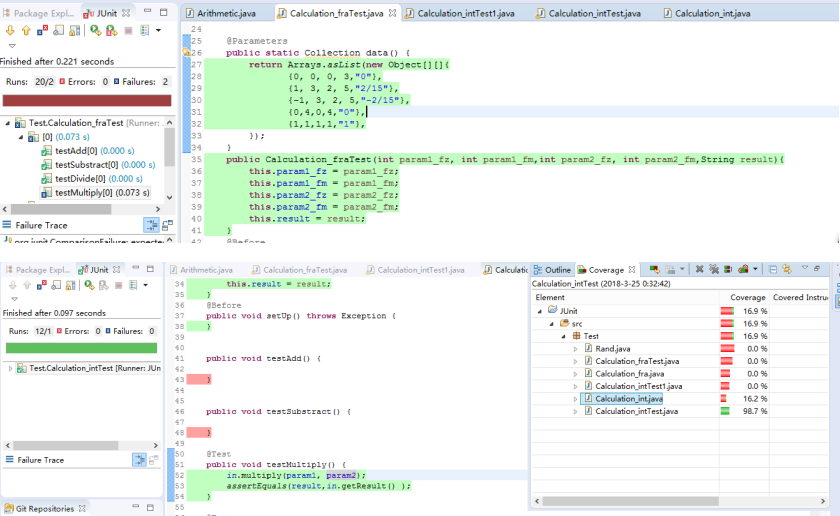
1.3原项目测试用例

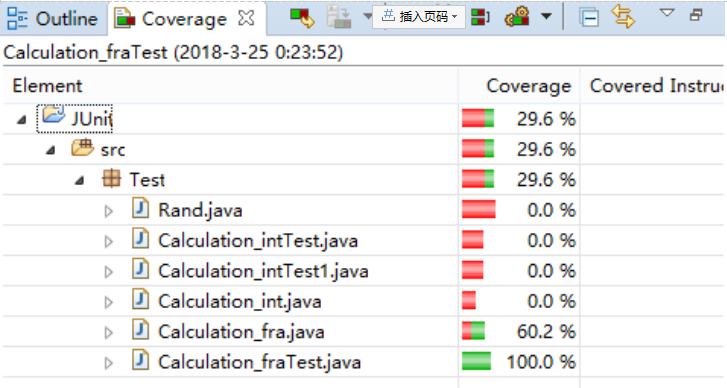
• （以整数和分数的乘法为例）原项目的单元测试分别对整数和分数的加减乘除进行测试，每个测试用了五个用例。

2、改进分析

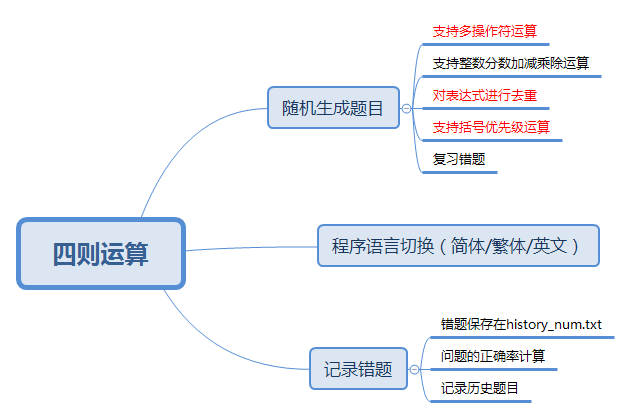
2.1改善部分

• 修改的代码中加入多操作符的运算
• 加入支持括号优先级运算
• 对表达式进行去重

2.2思维导图

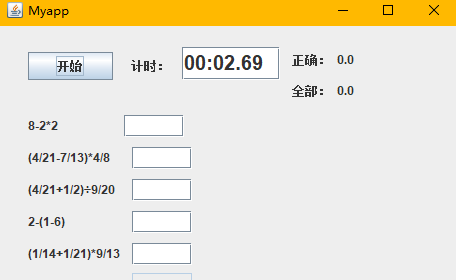
2.3支持括号优先级运算

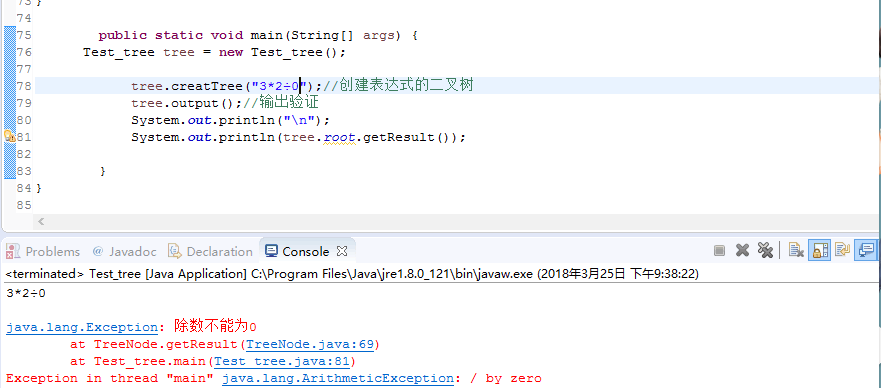
2.4算式去重

• 暂时还没实现，但是写的算法大概如下：

 int Isomorphic(Tree t1,Tree t2){
     if((t1==NULL)&&(t2==NULL))return 1;//都为空
     if(((t1==NULL)&&(t2!=NULL))||((t1!=NULL)&&(t2==NULL))) return 0;//一个为空另一个不为空
     if(t1->root!=t2->root) return 0;//根节点的值不一样
     if((t1->lchild==NULL)&&(t2->lchild==NULL)) return Isomorphic(t1->lchild,t2->rchild);
     if(((t1->lchild!=NULL)&&(t2->lchild!=NULL))&&(t1->lchild->data==t2->lchild->data))//没有交换
         return (Isomorphic(t1->lchild,t2->lchild)&&Isomorphic(t1->rchild,t2->rchild));//如果两个都不为空且左儿子相等，应该递归的找左对应左，右对应右
     else
         return (Isomorphic(t1->lchild,t2->rchild)&&Isomorphic(t1->rchild,t2->lchild));//否则就是交换了，递归的判断左对应右，右对应左

 };

2.5测试用例

• 新功能测试用例

3、PSP表格

PSP2.1	个人开发流程	预估耗费时间（分钟）	实际耗费时间（分钟）
Planning	计划	8	15
·Estimate	明确需求和其他相关因素，估计每个阶段的时间成本	8	6
Development	开发	240	284
·Analysis	需求分析 (包括学习新技术）	6	10
·Design Spec	生成设计文档	5	10
·Design Review	设计复审	4	15
·Coding Standard	代码规范	5	10
·Design	具体设计	20	30
·Coding	具体编码	288	300
·Code Review	代码复审	20	30
·Test	测试（自我测试，修改代码，提交修改）	15	25
Reporting	报告	9	10
·	测试报告	3	5
·	计算工作量	2	1
·	并提出过程改进计划	3	3

4、附加题

4.1支持乘方运算

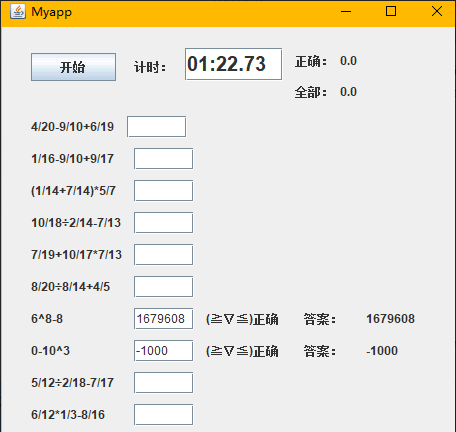
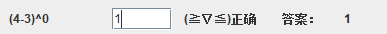
三、代码展示

BinaryTree类//构建二叉树
import java.util.ArrayList;

public class BinaryTree   
{  
      
    private TreeNode root;  
    private int num;  
    private ArrayList<TreeNode> opeList = new ArrayList<TreeNode>();  
      
    public BinaryTree(int num){  
        this.num = num;  
    }  
      
    public int getNum(){  
        return num;  
    }  
      
    public void setNum(int num){  
        this.num = num;  
    }  
      
    public void setTreeNode(TreeNode root){  
        this.root = root;  
    }  
      
      
    /** 
     * 获取最终的表达式，必须在CalAndVal()方法后调用 
     *  
     * @return str 
     */  
    public String toString(){  
        String str = root.toString();  
        str = str.substring(1, str.length()-1);  
        return str;  
    }  
      
    /** 
     * 计算并验证表达式 
     *  
     * @return result 
     */  
    public String CalAndVal(){  
        return root.getResult();  
    }  
      
    /** 
     * 计算二叉树的深度(层数)  
     *  
     * @return deep 
     */  
    public int getDeep(){  
        int i = this.num;  
        int deep = 2;  
        while(i/2 > 0){  
            deep++;  
            i /= 2;  
        }  
        return deep;  
    }  
      
    /** 
     * 生成二叉树 
     *  
     */  
    public void createBTree(){  
        TreeNode lchild, rchild, lnode, rnode;  
        int ran= Ran.getNumber(2),x,y;
        if(num == 1){
            if(ran==0){
                lchild = new TreeNode(String.valueOf(Ran.getNumber(10)), null, null);  
                rchild = new TreeNode(String.valueOf(Ran.getNumber(10)), null, null);  
            }
            else{
                x=Ran.getNumber(9)+1;
                y=Ran.getNumber(20)+1;
                for(int j=0;y<=x;j++){
                    y=Ran.getNumber(20)+1;
                }
                lchild = new TreeNode(String.valueOf(x)+"/"+String.valueOf(y), null, null); 
                x=Ran.getNumber(9)+1;
                y=Ran.getNumber(20)+1;
                for(int j=0;y<=x;j++){
                    y=Ran.getNumber(20)+1;
                }
                rchild = new TreeNode(String.valueOf(x)+"/"+String.valueOf(y), null, null); 
            }
            root = new TreeNode(String.valueOf(Ran.getOperator()), lchild, rchild);  
        }  
        else{  
            int num1 = 0;  
            int n = getDeep() - 3;  
            boolean[] place = Ran.getChildPlace(num);  
            root = new TreeNode(String.valueOf(Ran.getOperator()), null, null);  
            opeList.add(root);  
            for(int i = 0; i < n; i++){  
                for(int j = 0; j < (int)Math.pow(2, i); j++, num1++){  
                    lchild = new TreeNode(String.valueOf(Ran.getOperator()), null, null);  
                    rchild = new TreeNode(String.valueOf(Ran.getOperator()), null, null);  
                    opeList.get(j + num1).setChild(lchild, rchild);  
                    opeList.add(lchild);  
                    opeList.add(rchild);  
                }  
            }  
            for(int i = 0; i < place.length; i++){  
                if(place[i]){  
                    if(ran==0){
                        lnode = new TreeNode(String.valueOf(Ran.getNumber(10)), null, null);  
                        rnode = new TreeNode(String.valueOf(Ran.getNumber(10)), null, null);  
                    }
                    else{
                        x=Ran.getNumber(9)+1;
                        y=Ran.getNumber(20)+1;
                        for(int j=0;y<=x;j++){
                            y=Ran.getNumber(20)+1;
                        }
                        lnode = new TreeNode(String.valueOf(x)+"/"+String.valueOf(y), null, null); 
                        x=Ran.getNumber(9)+1;
                        y=Ran.getNumber(20)+1;
                        for(int j=0;y<=x;j++){
                            y=Ran.getNumber(20)+1;
                        }
                        rnode = new TreeNode(String.valueOf(x)+"/"+String.valueOf(y), null, null); 
                    }
                    if(i%2 == 0){  
                        lchild = new TreeNode(String.valueOf(Ran.getOperator()), lnode, rnode);  
                        opeList.add(lchild);  
                        opeList.get(num1).setLchild(lchild);  
                    }  
                    else{  
                        rchild = new TreeNode(String.valueOf(Ran.getOperator()), lnode, rnode);  
                        opeList.add(rchild);  
                        opeList.get(num1).setRchild(rchild);  
                    }  
                }  
                else{  
                    if(i%2 == 0){  
                        if(ran==0){
                            lchild=new TreeNode(String.valueOf(Ran.getNumber(10)), null, null);         
                        }
                        else{
                            x=Ran.getNumber(9)+1;
                            y=Ran.getNumber(20)+1;
                            for(int j=0;y<=x;j++){
                                y=Ran.getNumber(20)+1;
                            }
                            lchild = new TreeNode(String.valueOf(x)+"/"+String.valueOf(y), null, null); 
                        }  
                        opeList.get(num1).setLchild(lchild);  
                    }  
                    else{  
                
                            if(ran==0){
                                rchild = new TreeNode(String.valueOf(Ran.getNumber(10)), null, null);          
                            }
                            else{
                                x=Ran.getNumber(9)+1;
                                y=Ran.getNumber(20)+1;
                                for(int j=0;y<=x;j++){
                                    y=Ran.getNumber(20)+1;
                                }
                                rchild = new TreeNode(String.valueOf(x)+"/"+String.valueOf(y), null, null); 
                            }  
                        opeList.get(num1).setRchild(rchild);  
                         
                    }  
                num1 = num1 + i%2;  
            }  
        }  
    }  
}  
}

TreeNode类//树节点类，并进行递归计算
public class TreeNode {  
      
    private String str;  
    private TreeNode rchild = null;  
    private TreeNode lchild = null;  
      
    public TreeNode(String str){  
        this.str = str;  
    }  
      
    public TreeNode(String str, TreeNode lchild, TreeNode rchild){  
        this.str = str;  
        this.rchild = rchild;  
        this.lchild = lchild;  
    }  
      
    public void setChild(TreeNode lchild, TreeNode rchild){  
        this.lchild = lchild;  
        this.rchild = rchild;  
    }  
      
    public TreeNode getRchild() {    
        return rchild;    
    }    
    public void setRchild(TreeNode rchild) {    
        this.rchild = rchild;    
    }    
    public TreeNode getLchild() {    
        return lchild;    
    }    
    public void setLchild(TreeNode lchild) {    
        this.lchild = lchild;    
    }  
      
    public String getStr(){  
        return str;  
    }  
      
    /** 
     * 获取每个节点的运算结果，并检验除法 
     * 1)除数为0 
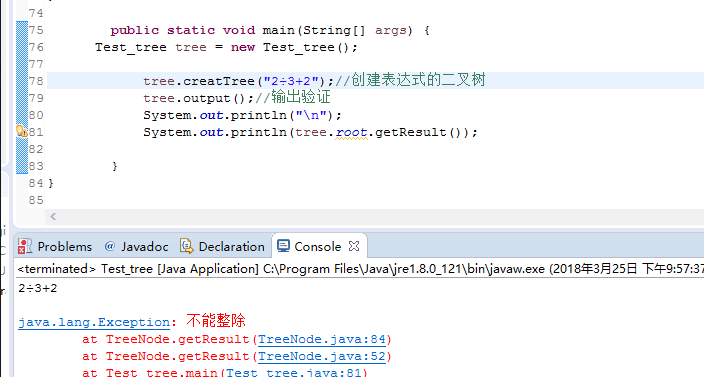
     * 2)不能整除 //不考虑，允许分数的出现
     * 出现以上两种情况的话将该运算符转换成其他三种运算符 
     *  
     * @return result 
     */  
    public String getResult(){  
        Compute com=new Compute();
        if(hasChild()){  
            switch(str){  
                case "+":
                    if(!getLchild().getResult().contains("/"))
                        return String.valueOf(Integer.parseInt(getLchild().getResult()) + Integer.parseInt(getRchild().getResult())); 
                    else
                        return com.Add(getLchild().getResult(),getRchild().getResult());
                case "-":  
                    if(!getLchild().getResult().contains("/"))
                        return String.valueOf(Integer.parseInt(getLchild().getResult()) - Integer.parseInt(getRchild().getResult()));  
                    else
                        return com.Subtract(getLchild().getResult(),getRchild().getResult());
                case "*":  
                    if(!getLchild().getResult().contains("/"))
                        return String.valueOf(Integer.parseInt(getLchild().getResult()) * Integer.parseInt(getRchild().getResult()));  
                    else    
                        return com.Multiply(getLchild().getResult(),getRchild().getResult());
                case "÷":  
                    if(getRchild().getResult().equals("0")||getRchild().getResult().contains("0/")){  
                        while(str.equals("÷")){  
                            str = String.valueOf(Ran.getOperator());  
                        }  
                        return this.getResult();  
                    }   
              
                    else{
                        if(!getLchild().getResult().contains("/")){
                            if(Integer.parseInt(getLchild().getResult()) % Integer.parseInt(getRchild().getResult()) != 0){  
                                while(str.equals("÷")){  
                                    str = String.valueOf(Ran.getOperator());  
                                }  
                                return this.getResult();  
                            }
                            else 
                                return String.valueOf(Integer.parseInt(getLchild().getResult()) / Integer.parseInt(getRchild().getResult())); 
                        }
                            
                        else{
                            
                            return com.Divide(getLchild().getResult(),getRchild().getResult());
                        }
                            
                    }
                case "^":
                    if(!getLchild().getResult().contains("/")){
                        if(Math.pow(Double.parseDouble(getLchild().getResult()),Double.parseDouble(getRchild().getResult()))<1){
                            while(str.equals("^")){  
                                str = String.valueOf(Ran.getOperator());  
                            }  
                            return this.getResult();
                        }
                        else
                            return String.valueOf((new Double (Math.pow(Double.parseDouble(getLchild().getResult()),Double.parseDouble(getRchild().getResult())))).intValue()); 
                    }
                        
                    else{
                        while(str.equals("^")){  
                            str = String.valueOf(Ran.getOperator());  
                        }  
                        return this.getResult();
                    }
                    
                    
                        
            }  
        }  
        return str;  
    }       
      
    /** 
     * 先对每个运算式添加括号，然后根据去括号法则，去掉多余的子式的括号 
     *  
     * @return string 
     */  
    public String toString(){  
        String Lstr = "", Rstr = "", Str = "";  
        if(hasChild()){  
            //右子树如果有孩子，说明右子树是一个表达式，而不是数字节点。  
            if(getRchild().hasChild()){                           
                //判断左邻括号的运算符是否为'/'  
                if(str.equals("÷")||str.equals("^")){  
                    //获取右子树的表达式，保留括号  
                    Rstr = getRchild().toString();                
                }  
                //判断左邻括号的运算符是否为'*'或'-'  
                else if(str.equals("*") || str.equals("-")){  
                    //判断op是否为'+'或'-'  
                    if(getRchild().str.equals("+") || getRchild().str.equals("-")){   
                        Rstr = getRchild().toString();            
                    }  
                    else{  
                        //获取右子树的表达式，并且去括号   
                        Rstr = getRchild().toString().substring(1, getRchild().toString().length()-1);    
                    }  
                }  
                else{  
                    //右子树除此之外都是可以去括号的。  
                    Rstr = getRchild().toString().substring(1, getRchild().toString().length()-1);        
                }  
            }  
            else{  
                Rstr = getRchild().str;  
            }  
            //左子树的情况同右子树类似  
            if(getLchild().hasChild()){                                               
                if(str.equals("*") || str.equals("÷")){  
                    if(getLchild().str.equals("+") || getLchild().str.equals("-")){  
                        Lstr = getLchild().toString();  
                    }  
                    else{  
                        Lstr = getLchild().toString().substring(1, getLchild().toString().length()-1);  
                    }  
                }  
                else{  
                    Lstr = getLchild().toString().substring(1, getLchild().toString().length()-1);  
                }  
            }  
            else{  
                Lstr = getLchild().str;  
            }  
            //获取当前的运算式，并加上括号  
            Str = "(" + Lstr + str + Rstr + ")";                                      
        }  
        else{  
            //若没有孩子，说明是数字节点，直接返回数字  
            Str = str;  
        }  
        return Str;  
    }  
      
    public boolean hasChild(){  
        if(lchild == null && rchild == null)  
            return false;  
        else  
            return true;  
    }  
}  

Compute类//对分数进行计算
public class Compute {
    
    public String Add(String str1,String str2){
        int mol1,mol2,den1,den2;
        int mol,den;
        mol1=Integer.parseInt(Trans(str1)[0]);
        den1=Integer.parseInt(Trans(str1)[1]);
        mol2=Integer.parseInt(Trans(str2)[0]);
        den2=Integer.parseInt(Trans(str2)[1]);
        mol=mol1*den2+mol2*den1;
        den=den1*den2;
        int gcd=Compute.GCD(mol,den);
        mol/=gcd;
        den/=gcd;
        return(mol+"/"+den);
    }
    public String Subtract(String str1,String str2){
        int mol1,mol2,den1,den2;
        int mol,den;
        mol1=Integer.parseInt(Trans(str1)[0]);
        den1=Integer.parseInt(Trans(str1)[1]);
        mol2=Integer.parseInt(Trans(str2)[0]);
        den2=Integer.parseInt(Trans(str2)[1]);
        mol=mol1*den2-mol2*den1;
        den=den1*den2;
        int gcd=Compute.GCD(mol,den);
        mol/=gcd;
        den/=gcd;
        return(mol+"/"+den);
    }
    public String Multiply(String str1,String str2){
        int mol1,mol2,den1,den2;
        int mol,den;
        mol1=Integer.parseInt(Trans(str1)[0]);
        den1=Integer.parseInt(Trans(str1)[1]);
        mol2=Integer.parseInt(Trans(str2)[0]);
        den2=Integer.parseInt(Trans(str2)[1]);
        mol=mol1*mol2;
        den=den1*den2;
        int gcd=Compute.GCD(mol,den);
        mol/=gcd;
        den/=gcd;
        return(mol+"/"+den);
    }
    public String Divide(String str1,String str2){
        int mol1,mol2,den1,den2;
        int mol,den;
        mol1=Integer.parseInt(Trans(str1)[0]);
        den1=Integer.parseInt(Trans(str1)[1]);
        mol2=Integer.parseInt(Trans(str2)[0]);
        den2=Integer.parseInt(Trans(str2)[1]);
        mol=mol1*den2;
        den=den1*mol2;
        int gcd=Compute.GCD(mol,den);
        mol/=gcd;
        den/=gcd;
        return(mol+"/"+den);
    }
    public static String[] Trans(String str){
        String[] strArray=new String[2];
        for(int i=0;i<str.length();i++){
            if(str.charAt(i)=='/'){
                strArray[0]=str.substring(0,i);
                strArray[1]=str.substring(i+1,str.length());
                break;
            }   
        }
        return strArray;
    }
    public static int GCD(int a,int b) {
        if(b==0)
            return a;
        else
            return GCD(b,a%b);
    }
}

QA_List类//输出界面根据题数调用式子及返回结果

import java.util.ArrayList;
import java.util.List;
import java.util.Random;

public class QA_List {

    public static int i;
    public static List<String> Qusetion=new ArrayList<String>();
    public static List<String> Answer=new ArrayList<String>();
    public QA_List(){
        for(int a=0;a<i;a++)
        {

            BinaryTree bTree;  

                bTree = new BinaryTree(2);//随机生成数与表达式的数字个数有关  
                bTree.createBTree();  
                String result = bTree.CalAndVal();
                if(result.contains("/")){
                    if(Compute.Trans(result)[0].equals("0")){
                        result="0";
                    }else if(Compute.Trans(result)[1].equals("1")){
                        result=Compute.Trans(result)[0];
                    }
                }
                Answer.add(result);
                Qusetion.add(bTree.toString());
    
        }
     for(int a=0;a<(10-i);a++){
        Answer.add("");
        Qusetion.add("");
     }
    }
     
}

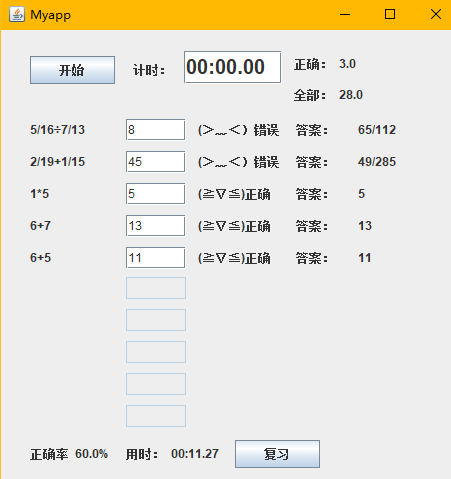
四、程序运行

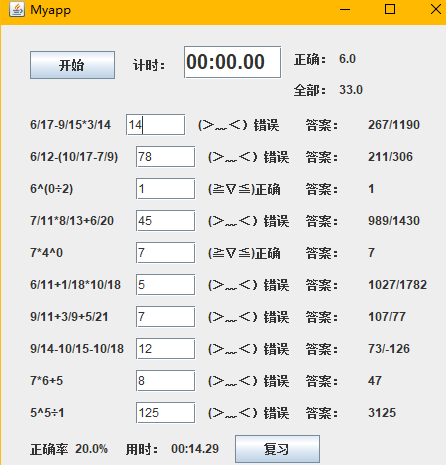
五、小结感受

1、结对照片

2、结对编程真的能够带来1+1>2的效果吗？通过这次结对编程，请谈谈你的感受和体会。

• 我觉得结对编程确实有1+1>2的效果。编程过程有时候出现的bug怎么找都找不到，都说旁观者清，说不定在小伙伴的检查下能够有意想不到的收获；编程的整个算法思路能够有人一起沟通，可以择较优者进行编程，会事半功倍。遇到困难时，有个人能够互相勉励，还是挺不错的。

  3、码云提交记录截图

  
  

来源：https://www.cnblogs.com/qxx-Ultraman/p/8641943.html