深度学习入门知识梳理（四）：卷积神经网络（CNN）

文章目录

• 前言
• 1、卷积层
• 1.1、卷积运算
• 1.2、填充
• 1.3、步幅
• 2、池化层
• 2.1 池化层的特征
• 2.1 池化层的功能

前言

  在卷积神经网络（CNN）中，卷积层的输入输出数据称为特征图。对应的，卷积层的输入数据称为输入特征图，输出数据称为输出特征图。
  相较于全连接神经网络，卷积神经网络有两个比较大的特点：
  （1）卷积网络有至少一个卷积层，用来提取特征。
  （2）卷积网络的卷积层通过权值共享的方式进行工作，大大减少权值 的数量，使得在训练中在达到同样识别率的情况下收敛速度明显快于全连接网络。

1、卷积层

1.1、卷积运算

  参考文章链接：如何通俗易懂地解释卷积
  一维卷积的数学定义如下：
$h(x)=\int_{-\infty}^{+\infty} f(\alpha)g(x-\alpha)d\alpha=f(x)*g(x) \tag{1-1}$
  可以从信号处理角度理解(需要有信号处理基础)：f(x)为系统输入信号，g(x)为单位脉冲响应，h(x)为系统输出响应。其实质就是一个翻转、滑动、加权叠加的过程，非常生动形象。
  二维卷积的数学定义如下：
$h(x,y)=\int_{-\infty}^{+\infty}\int_{-\infty}^{+\infty} f(m,n)g(x-m,y-n)dmdn=f(x,y)*g(x,y) \tag{1-2}$
  二维离散卷积的数学定义如下：
$h(x,y)=\sum_{m=0}^{M-1} \sum_{n=0}^{N-1}f(m,n)g(x-m,y-n)=f(x,y)*g(x,y) \tag{1-3}$
  在图像处理中，f(x)对应输入数据，g(x)对应滤波器，h(x)对应输出特征图。卷积运算可以理解为：随着窗口的滑动，g(x) 对输入图像进行取样，或者称为特征提取的过程。下图展示了图像卷积过程（其中，把g矩阵旋转了180°）。

  卷积神经网络中，卷积层进行的处理就是卷积运算。这里的卷积运算比图像处理中的卷积运算多加上一个偏置。即：
$\begin{cases} h_1(x,y)=\sum_{i=0}^{I-1}\sum_{m=0}^{M-1} \sum_{n=0}^{N-1}f(i,m,n)g_1(i,x+m,y+n) +b _1\\ h_2(x,y)=\sum_{i=0}^{I-1}\sum_{m=0}^{M-1} \sum_{n=0}^{N-1}f(i,m,n)g_2(i,x+m,y+n) +b _2 \\ \quad \quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\cdots \cdots \cdots\\ h_n(x,y)=\sum_{i=0}^{I-1}\sum_{m=0}^{M-1} \sum_{n=0}^{N-1}f(i,m,n)g_n(i,x+m,y+n) +b _n \end{cases} \tag{1-4}$
  图像是3维数据，除了高、长方向之外，还需要处理通道方向。当通道方向上有多个特征图时，会按通道进行输入数据和滤波器的卷积运算，并将结果相加，最后加上偏置，从而得到输出。
  例如，处理三维彩色RGB图像时，其包含有R、G、B三个通道，每个通道都需要对应一个滤波器，经过卷积运算后结果对应相加，再加上偏置信项，最终输出一个通道的特征图。若想要输入n个通道的特征图，则需要n组类似结构。
  我们可以在经典动图（图片来源于CS231n）的基础上深入理解卷积神经网络卷积层的卷积运算。

  从上图可以看出，对于输入特征图，卷积运算在特征图上以一定间隔滑动窗口，窗口和卷积核（滤波器）之间位置一一对应，其元素相乘后再相加求和(此计算也被称为乘积累加运算)，最后加上偏置，并将运算结果输出到输出特征图的对应位置。

1.2、填充

  在进行卷积层的处理之前，有时要向输入数据的周围填入固定的数据（比如0等），这称为填充（padding），是卷积运算中经常会用到的处理。
  在下图的例子中，对大小为(4, 4)的输入数据应用了幅度为1的填充。“幅度为1的填充”是指用幅度为1像素的0填充周围。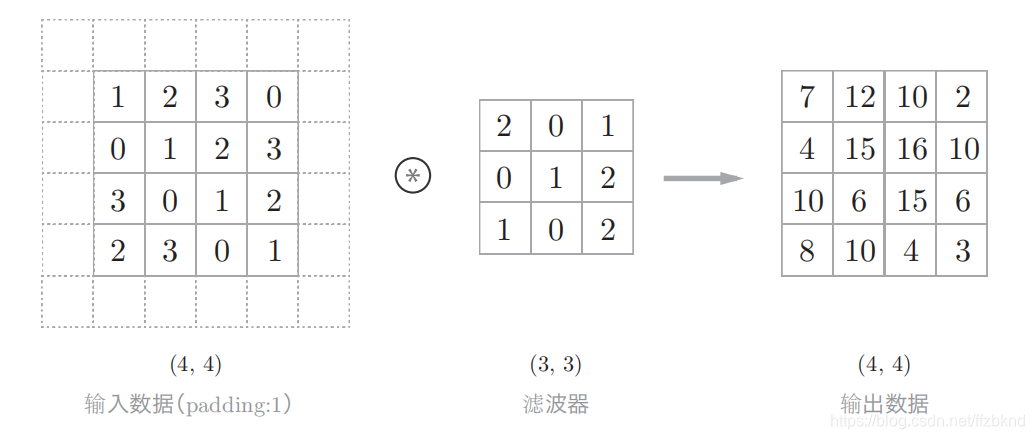

  使用填充主要是为了调整输出特征图的大小。

1.3、步幅

  窗口（目标区域）滑动的距离称为步幅（stride）。下图是步幅设为2的例子。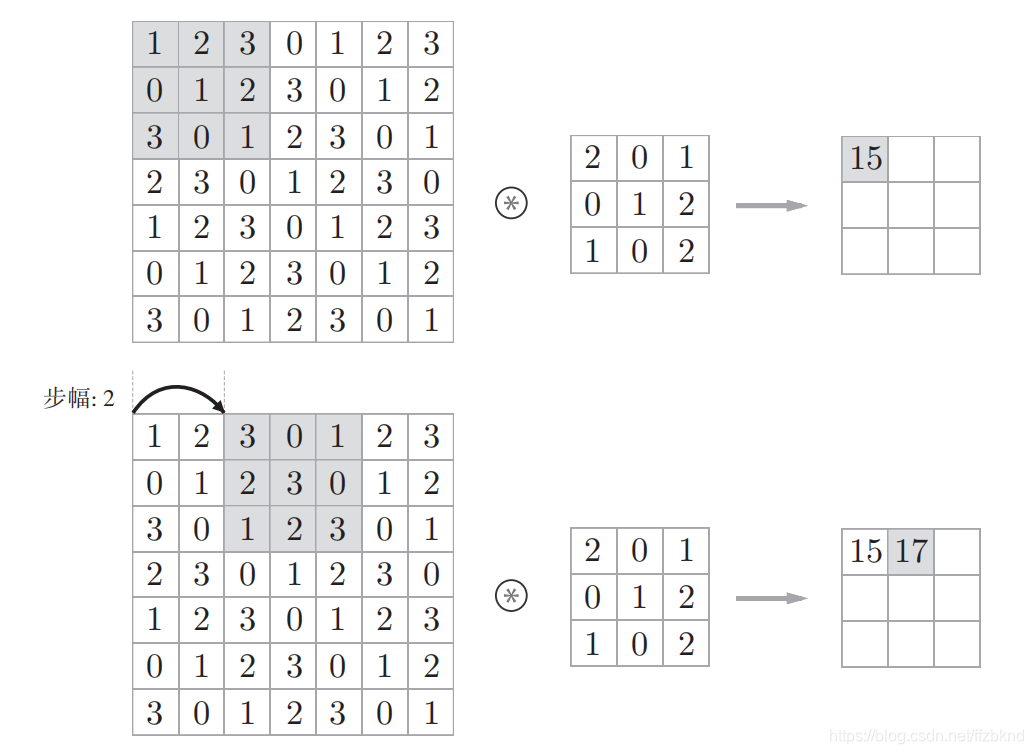

  增大步幅后，输出大小会变小。而增大填充后，输出大小会变大。
  对于卷积运算，设输入特征图尺寸大小为$(H, W)$,卷积核的大小为$(FH,FW)$，输出特征图大小为$(OH,OW)$，填充为$P$，步幅为$S$。输出特征图的大小可通过下列公式计算。
$OH = \frac{H+2P-FH}{S}+1 \tag{1-1}$
$OW = \frac{W+2P-FH}{S}+1 \tag{1-2}$

2、池化层

  池化层（Pooling Layer）实际上是对 Feature Map再进行了一次数据处理。
  池化层常用的数据处理有两种：
Max池化：计算目标区域的最大值。
Average池化：计算目标区域的平均值。

2.1 池化层的特征

  一、没有要学习的参数
  池化层和卷积层不同，没有要学习的参数。池化只是从目标区域中取最大值（或者平均值），所以不存在要学习的参数。
  二、通道数不发生变化
  经过池化运算，输入数据和输出数据的通道数不会发生变化，计算是按通道独立进行的。
  三、对微小的位置变化具有鲁棒性（健壮）
  输入数据发生微小偏差时，池化仍会返回相同的结果。因此，池化对输入数据的微小偏差具有鲁棒性。

2.1 池化层的功能

  第一，它又进行了一次特征提取，能够减小下一层数据处理量。
  第二，由于这个特征的提取，能够有更大的可能性进一步获取更为抽象的信息，从而
防止过拟合，或者说提高一定的泛化性。
  第三，由于这种鲁棒性，所以能够对输入的微小产生更大的容忍，也就是保持其不变性这里的容忍包括图形的少量平移 旋转以及缩放等变化。
  注：池化层在 CNN 网络中不是一个必需的组件。

来源：CSDN

作者：冰塘麻辣鱼

链接：https://blog.csdn.net/ffzbknd/article/details/102307449