矩阵连乘问题

由于矩阵乘法运算满足结合率，如果有矩阵A、B、C、D连续相乘，那么 A(BCD) = (AB)(CD) = … 。
所以可以找到一个好的加括号顺序使得计算量减少。可以使用动态规划问题解决。

动态规划解题步骤：
1， 找到最优子结构
即子问题最优可以令父问题也达到最优。本例中，若想(ABCDEFG)*(HIJKLMN)计算步骤最少，那么ABCDEFG加括号方式一定是最优的，同理HIJKLMN加括号也是最优的。可以尝试使用分治法（递归）先求出最优解。
2，使用空间换时间
使用一个空间保存子问题的解，另一个空间保存求解过程，计算某个子问题时，先判断子问题是否已经解决，如果已经解决，则直接返回已保存的解，否则计算这个子问题的解并存下。即，将上一步分治的计算结果存在一个数组里，并将分治的过程保存在另一个数组里。
3，找到最优解
根据保存的求解过程，找到最优解。

运行结果：

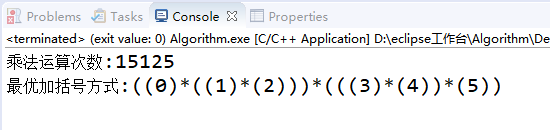
代码如下

#include <iostream>
using namespace std;

/* 递归求解最优的加括号方式
 * i 子问题下界
 * j 子问题上界
 * k 存储子问题的解
 * s 存储子问题求解过程
 * */
int mulSqlAct(int w[], int h[], int i, int j, int** k, int** s){
	if(j - i <= 1){
		return 0;
	}

	//动态规划：把子问题的解存下
	if(k[i][j] == 0){
		unsigned int min = 0xFFFFFFFF;
		unsigned int minIndex = 0;
		for(int p = i + 1; p < j; p++){

			int lValue = mulSqlAct(w, h, i, p, k, s);;
			int rValue = mulSqlAct(w, h, p, j, k, s);;
			int count = lValue + rValue + w[i] * h[j - 1] * w[p];
			if(count < min){
				min = count;
				minIndex = p;
			}
		}
		k[i][j] = min;
		s[i][j] = minIndex;
	}
	return k[i][j];
}

/* 找到最好的加括号方式
 * 即根据求解过程，找到问题的最优解
 * */
void trace(int** s, int i, int j){
	if(j - i <= 1){
		cout << i;
		return;
	}

	cout << "(";
	trace(s, i, s[i][j]);
	cout <<")" ;
	cout << "*";
	cout << "(" ;
	trace(s, s[i][j], j);
	cout << ")";
}

/* w 矩阵的长度
 * h 矩阵的宽度
 * n 相乘矩阵的个数
 * */
void mulSeq(int w[], int h[], int n){
	int** k = new int*[n + 1];
	int** s = new int*[n + 1];
	for(int i = 0; i <= n; i++){
		k[i] = new int[n + 1];
		s[i] = new int[n + 1];
		for(int j = 0; j <= n; j++){
			k[i][j] = 0;
			s[i][j] = 0;
		}
	}

	cout << "乘法运算次数:" << mulSqlAct(w, h, 0, n, k, s) << endl;
	cout << "最优加括号方式:";
	trace(s, 0, n);
}

int main()
{

	int w[] = {30, 35, 15, 5, 10, 20};
	int h[] = {35, 15, 5, 10, 20, 25};
	mulSeq(w, h, 6);
	return 0;
} 

来源：CSDN

作者：周者

链接：https://blog.csdn.net/u013749051/article/details/104062579