在数据结构中,树的定义如下:
树(tree)是n(n>=0)个节点的有限集,当n=0时,称为空树。在任意一个非空树中,有如下特点:
1.有且仅有一个特定的称为根的节点。
2.当n>1时,其余节点可分为m(m>0)个互不相交的有限集,每一个集合本身又是一个树,并称为根的子树。
树有以下概念:
根节点、父节点、兄弟节点、孩子节点。
树的最大层级数,被称为树的高度或深度。
二叉树:
二叉树(binary tree)是树的一种特殊形式。二叉,指的是这种树的每个节点最多有2个孩子节点。这里最多有2个,也可能只有1个,或者没有孩子节点。

二叉树的两个特殊概念:满二叉树和完全二叉树。
满二叉树:(每一个分支都是满的),所有非叶子节点都存在左右孩子,并且所有叶子节点都在同一层级上。
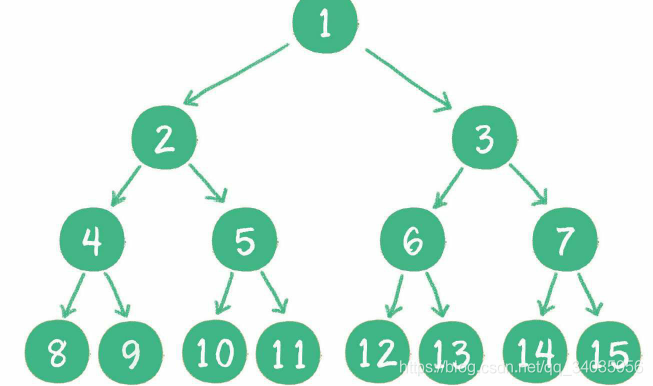
完全二叉树:对于一个有n个节点的二叉树,按层级顺序编号,则所有节点的编号为从1到n。如果这个树所有节点和同样深度的满二叉树的编号为从1到n的节点位置相同。则这个二叉树为完全二叉树。

二叉树可以用链式存储和数组两种物理存储结构来表达。
链式存储:

二叉树的一个节点最多指向左右两个孩子节点,所以二叉树一个节点包含3部分;
1.存储数据的data变量
2.指向左孩子的left指针
3.指向右孩子的right指针
使用数组存储:

使用数组存储时,会按照层级顺序把二叉树的节点放到数组中对应的位置上。如果某一个节点的左孩子和右孩子空缺,则数组的相应位置也空出来。
这样设计,可以更方便地在数组中定位二叉树的孩子节点和父节点。
假设一个父节点的下标是parent,那么它的左孩子节点下标就是2*parent+1;右孩子节点下标是2*parent+2。
反过来,一个左孩子的节点下标是leftChild,那么父节点下标就是(leftChild-1)/2。
二叉树的应用:
最主要的应用在于进行查找操作和维持相对顺序两个方面。
1.查找:二叉查找树(binary search tree)
二叉查找树在二叉树的基础上增加了以下几个条件:
1、若左子树不为空,则左子树所有节点的值均小于根节点的值;
2、若右子树不为空,则右子树所有节点的值均大于根节点的值;
3、左、右子树也都是二叉查找树。

对于一个节点分布相对均衡的二叉查找树,如果左节点总数是n,那么搜索节点的时间复杂度就是O(logn),和树的深度是一样的。
这种依靠比较大小来逐步查找的方式,和二分查找算法非常相似。
2.维持相对顺序
二叉查找树要求左子树小于父节点,右子树大于父节点,这样保证了二叉树的有序性,因此 二叉查找树也叫二叉排序树。
新插入的节点,遵循二叉排序树的原则:例如插入新元素5,由于5<6,5>3,5>4,所以5最终会插入到节点4的右孩子位置。

再如插入新元素10,由于10>6,10>8,10>9,所以10最终会插入到节点9的右孩子位置。

问题:如果依次插入9、8、7、6、5、4,就会让查询节点的时间复杂度退化成O(n)。

解决:二叉树的自平衡,如红黑树、ALV树、树堆等。
二叉堆:只要求父节点比它的左右孩子都大。
二叉树的遍历
从节点之间位置关系的角度看,二叉树的遍历可分为4种:
1.前序遍历:根节点、左子树、右子树。
2.中序遍历:左子树、根节点、右子树
3.后序遍历:左子树、右子树、根节点
4.层序遍历:一层一层遍历
从更宏观的角度看,二叉树的遍历归结为两大类。
1.深度优先遍历(前序遍历、中序遍历、后序遍历)。偏向于纵深,一头扎下去。
2.广度优先遍历(层序遍历)
前、中、后:



using System;
using System.Collections.Generic;
namespace CSharpTest01
{
public static class LinkedListExtension
{
public static int RemoveFirstEx(this LinkedList<int> list)
{
int value = Convert.ToInt32(list.First);
list.RemoveFirst();
return value;
}
}
public class TreeNode
{
public int data;
public TreeNode leftChild;
public TreeNode rightChild;
public TreeNode(int data)
{
this.data = data;
}
}
public class MyBinaryTree
{
/// <summary>
/// 创建二叉树
/// </summary>
public TreeNode CreateBinaryTree(LinkedList<int> inputList)
{
TreeNode node = null;
if (inputList == null || inputList.Count <= 0)
{
return null;
}
int data = inputList.RemoveFirstEx();
if (data != null)
{
node = new TreeNode(data);
node.leftChild = CreateBinaryTree(inputList);
node.rightChild = CreateBinaryTree(inputList);
}
return node;
}
/// <summary>
/// 二叉树前序遍历
/// </summary>
public void PreOrderTraveral(TreeNode node)
{
if(node == null)
{
return;
}
Console.WriteLine(node.data);
PreOrderTraveral(node.leftChild);
PreOrderTraveral(node.rightChild);
}
}
class Program
{
static void Main(string[] args)
{
Console.ReadLine();
}
}
}
来源:CSDN
作者:KERVEN_HKW
链接:https://blog.csdn.net/qq_34035956/article/details/104036671