【总结】矩阵快速幂

在学习矩阵快速幂之前，首先我们需要分别了解快速幂和矩阵乘法

快速幂

快速幂要求解的是这样一类问题：

给你A,B,C，求A的B次方模C的余数

A,C<=10^9,B<=10^18

如果我们线性去求，时间复杂度是O（n）的，但题目中给出的B是很大的数，这样显然会超时,我们可以用快速幂来加速这个过程。

我们可以想像一下小学的时候我们如何计算2^16

2^16=4^8=16^4=256^2=65536

那如何计算2^18呢？

2^18=4^9=44^8=416^4=4256^2=465536=262144

快速幂同理也是如此

我们可以按照上面做法，利用分治的思想求去解

这样原本O(n)的时间复杂度便降到了O(log n )

long long ans=1,base=a;
while(n>0){
        if(n&1){
            ans*=base;
        }
        base*=base;
        n=n/2;
    }

矩阵乘法

矩阵乘法可以先稍作了解，知道矩阵相乘的运算法则

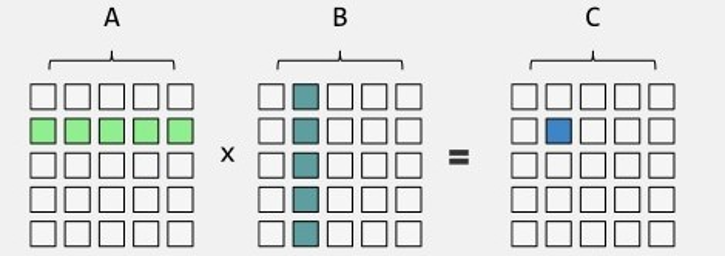
•\(C[i][j]= A[i][k]B[k][j]\)

矩阵快速幂

矩阵快速幂的原理同快速幂一样，只是转换为了矩阵之间的乘法操作

所以单纯的重载一下运算符，将普通的乘法转换为矩阵乘法就好了。

嗯，看一下代码就应该很好理解了x

#include<iostream>
#include<cstdio>
#include<cctype>
#define ll long long
#define Mod 1000000007
using namespace std;
ll read(){
    ll a=0;int f=0;char p=getchar();
    while(!isdigit(p)){f|=p=='-';p=getchar();}
    while(isdigit(p)){a=(a<<3)+(a<<1)+(p^48);p=getchar();}
    return f?-a:a;
}
ll n,k;
struct mat{
    ll m[101][101];
}a,b,c,e;
mat mul(mat x,mat y){
    mat k;
    for(int i=1;i<=n;i++)
        for(int j=1;j<=n;j++)
            k.m[i][j]=0;
    for(int i=1;i<=n;i++)
        for(int j=1;j<=n;j++)
            for(int q=1;q<=n;q++)
                k.m[i][j]=k.m[i][j]%Mod+x.m[i][q]%Mod*y.m[q][j]%Mod;
    return k;
}
mat pow(mat x,ll y){
    mat ans=b;
    while(y){
        if(y&1)ans=mul(ans,x);
        x=mul(x,x);
        y>>=1;
    }
    return ans;
}
int main(){
    n=read();k=read();
    for(int i=1;i<=n;i++)
        for(int j=1;j<=n;j++)
            a.m[i][j]=read();
    for(int i=1;i<=n;i++)b.m[i][i]=1;
    mat ans=pow(a,k);
    for(int i=1;i<=n;i++){
        for(int j=1;j<=n;j++)
            cout<<ans.m[i][j]%Mod<<" "; 
        cout<<endl;
    }
}

来源：https://www.cnblogs.com/huixinxinw/p/12207565.html