普利姆算法解决最小生成树问题

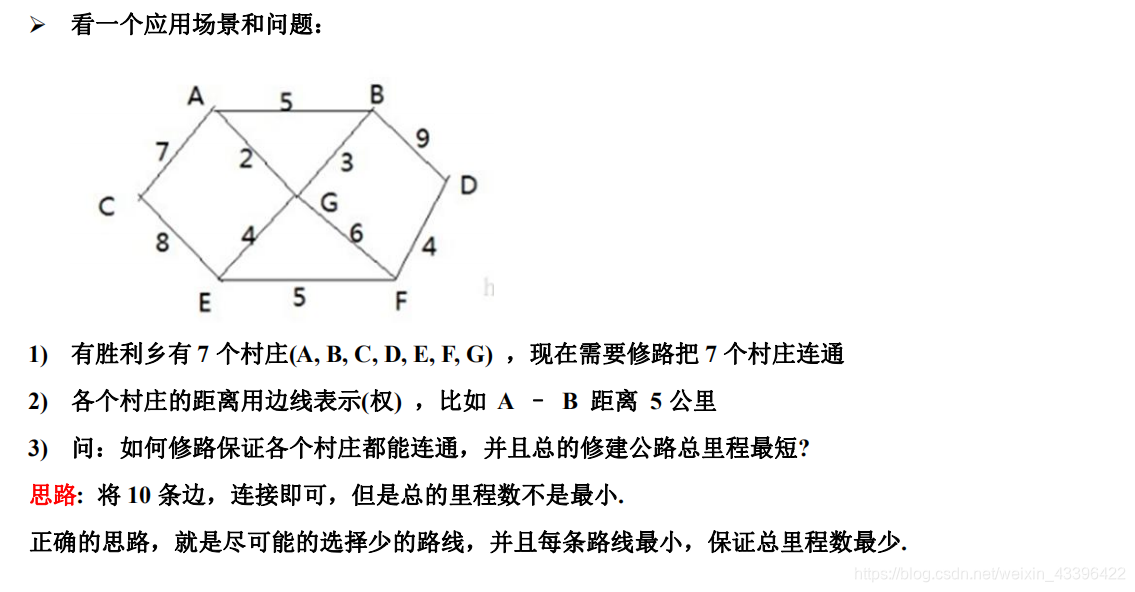
普利姆算法就是从第一个顶点出发，每次都选择已访问节点的最短相邻节点，最后将所有节点都访问，代码：

/**
 * 普利姆算法解决最小生成树问题
 */
public class PrimAlgorithm {
    public static void main(String[] args) {
       char[] data = {'A','B','C','D','E','F','G'};
       int verx = data.length;
       //二维数组表示邻接矩阵，10000表示两点不连通
       int[][] weight = {
               {10000,5,7,10000,10000,10000,2},
               {5,10000,10000,9,10000,10000,3},
               {7,10000,10000,10000,8,10000,10000},
               {10000,9,10000,10000,10000,4,10000},
               {10000,10000,8,10000,10000,5,4},
               {10000,10000,10000,4,5,10000,6},
               {2,3,10000,10000,4,6,10000}
       };

        MGraph mGraph = new MGraph(verx);
        MinTree minTree = new MinTree();
        minTree.createMGraph(mGraph,verx,data,weight);
        minTree.printMGraph(mGraph);
        //测试普利姆算法
        minTree.createMinTree(mGraph,0);
    }
}

//最小生成树
class MinTree{
    /**
     * 生成图的方法
     * @param mGraph  图对象
     * @param verx    图顶点个数
     * @param data    顶点数据
     * @param weight   图的邻接矩阵
     */
   public void createMGraph(MGraph mGraph,int verx,char[] data,int[][] weight){
       for(int i = 0;i<verx;i++){
           mGraph.data[i] = data[i];
           for(int j = 0;j<verx;j++){
               mGraph.weight[i][j] = weight[i][j];
           }
       }
   }

   //输出图的邻接矩阵的方法
    public void printMGraph(MGraph mGraph){
       for(int[] link:mGraph.weight){
           System.out.println(Arrays.toString(link));
       }
    }

    /**
     * 生成最小生成树
     * @param mGraph  图对象
     * @param v       表示从哪个顶点开始
     */
    public void createMinTree(MGraph mGraph,int v){
        //记录已经被访问过的顶点，默认为0，还没访问
        int[] visited = new int[mGraph.verx];
        //记录两个被连接的顶点
        int h1 = -1;
        int h2 = -1;
        int min = 10000;//记录每次遍历时，最短路径，初始值为10000
        //初始顶点设置为已访问
        visited[v] = 1;
        for(int k = 1;k<mGraph.verx;k++){//表示verx个顶点 需要 verx-1条边,所以循环verx-1次
            //遍历所有顶点
            for(int i = 0;i<mGraph.verx;i++){
                for(int j = 0;j<mGraph.verx;j++){
                    //表示筛选出已经访问过的节点  的未访问的邻节点，并且边最小的两个顶点
                    if(visited[i] == 1 && visited[j] == 0 && mGraph.weight[i][j]<min){
                        min = mGraph.weight[i][j];
                        h1 = i;
                        h2 = j;
                    }
                }
            }
            //找到一条边是最小的
            System.out.println("边<"+mGraph.data[h1]+","+mGraph.data[h2]+">:权值"+min);
            //将h1,h2设置为已访问
            visited[h2] = 1;
            //重置min
            min = 10000;
        }

    }
}

//图
class MGraph{
    int verx;//表示图节点的个数
    char[] data;//存放节点
    int[][] weight;//存放边，就是邻接矩阵

    public MGraph(int verx) {
        this.verx = verx;
        data = new char[verx];
        weight = new int[verx][verx];
    }
}

来源：CSDN

作者：疯狂的小蜗

链接：https://blog.csdn.net/weixin_43396422/article/details/104009041