最短路径 | 易学教程

在这里插入图片描述

要求最短的路径，首先得把这些边都存储起来，边的存储有邻接表和邻接矩阵两种，这个题数据最大20万个，用邻接矩阵肯定不行，只能使用邻接表来存储。
求最短路的算法 Dijkstra，Floyd，Bellman，spfa；
这个题想要100%通过测试用例，只能使用效率高但是不是很稳定的spfa算法。
需要注意的是，初始化给所有路径的长度定义的无穷大这个数值，不能太大，也不能太小，比如说0x3fffffff，具体大小根据题中所给的边权的范围来定。

Dijkstra（迪杰斯特拉）算法

Dijkstra算法所求的是单源的最短路径，从起点开始，每一次都找到当前起点的最短可到达的点，然后再进行松弛。
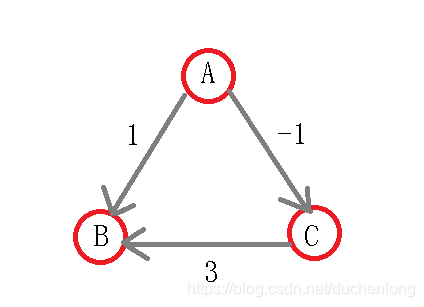
该算法在使用时要求所包括的边中不能有负权边。

这可以看出，原本A -> B最短路径应该是 1 ，如果存在负权边的话就变成了2

#define MAXN 1000 //最大顶点数
#define INF 0x3fffffff //一个很大的数 

int n = 0, m = 0, s = 0;//n为顶点数 m为边数 s为起点 
int d[MAXN] = {0}; //起点到各点最短路径的长度
int visit[MAXN] = {0};//记录已经找到的最短路径的点 0--》未找到  1--》表示找到
int arr[MAXN][MAXN] = {0}; //暂时用邻接矩阵来存储各个边

void Dijkstra()
{
	int i = 0;
	//初始化一步可以到达的路径长度 
	for(i = 0;i < n;i++)
	{
		if(arr[s][i])
		{
			d[i] = 	arr[s][i];
		}
		else
		{
			d[i] = INF;
		}
	}
	visit[s] = 1;//起点写进数组中
	d[s] = 0; //自己到自己的路径设置为0 

	for(i = 0;i < n; i++)
	{
		//找到一条最短的路 
		int j = 0,u = -1,min = INF;
		for(j = 0; j < n; j++)
		{
			//如果存在一条最短路径，并且该点没有被访问，更新min 和 u
			if(!visit[j] && d[j] < min)
			{
				u = j;
				min = d[j];
			}
		}
		//如果 u 的值还是初值，就说明已经找完了
		if(u == -1)
		{
			return ;
		}

		visit[u] = 1;
		d[u] = min;

		//更新路径 
		for(j = 0;j < n;j++)
		{
			if(!visit[j] && arr[u][j] && d[u] + arr[u][j] < d[j])
			{
				d[j] = d[u] + arr[u][j];
			}
		}
	}
}

Floyd（弗洛伊德）算法

可以解决多源的最短路径问题，可以正确处理有向图或者负权边的最短路径问题。
问题就是，该算法的时间复杂度为O（n 3），空间复杂度是O（n 2）。
寻找从节点i 到 j 的最短路径有两种情况，1是直接从i到j，2是从i开始，经过若干个点，最后到j。如果说dis[i][j] 是i到j目前的最短路径，那么对于每一个非i，j的节点k，都要检查dis[i][k] + dis[k][j] < dis[i][j] 是否成立，如果成立，则对该边进行松弛，这样的话，遍历完所有结点，dis[i][j] 就是最短的路径了，就不用担心负权边的问题。

#define MAX 10005

int arc[1000][1000]={0};

void Floyd(int n)
{
	int i=0;	
	int j=0;
	int k=0;
	for(k=0;k<n;k++)
	{
		for(i=0;i<n;i++)
		{
			for(j=0;j<n;j++)
			{
				if(arc[i][k]!=MAX && arc[k][j]!=MAX)
				{
					if(arc[i][j] > arc[i][k]+arc[k][j])
					{
						arc[i][j] = arc[i][k]+arc[k][j];
					}
				}
				
			}
		}
	}
	
}

Bellman算法

该算法是求含负权图的单元最短路径的一种算法，效率较低（O(nm)）。
原理就是连续进行松弛，在每次松弛是把每一条边都更新一下，若在n-1次松弛后还能更新，则说明图中含有负环，所以就无法完成求最短路径的结果。所以说可以判断图中是否含有负环的一种算法。

#define MAX 0xffff
#define MAX_ARR 200005

typedef struct Side
{
	int _from;//边的起点
	int _to;//边的终点
	int _key;//边的权值
}Side;

Side side[MAX_ARR] = { 0 };//结构体数组来存放每一条边
int dis[MAX_ARR] = { 0 };//存放最短的路径

//n是顶点数目 m是边的数目
void BellMan(int n, int m)
{
	int i = 0, j = 0;
	int key = 0;
	int temp = 0;
	Side p;
	
	for (i = 2; i <= n; i++)
	{
		dis[i] = MAX;
	}
	dis[1] = 0;

	for (i = 1; i < n; i++)
	{
		for (j = 0; j < m; j++)
		{
			p = side[j];
			temp = dis[p._from] + p._key;
			//对可以优化的路径进行松弛
			if (temp < dis[p._to])
			{
				dis[p._to] = temp;
			}
		}
	}
	//判断有无负环
	for (j = 0; j < m; j++)
	{
		p = side[j];
		temp = dis[p._from] + p._key;
		if (temp < dis[p._to])
		{
			printf("存在负环\n");
			return ;
		}
	}
}

spfa算法

适用的范围：给定的图存在负权边，这时Dijkstra算法便不能使用，题目对时间复杂度有所要求，这时Bellman-ford的时间复杂度又很高，这时就可以使用spfa算法。
算法思想：用一个数组来记录每个节点的最短路径，邻接表来存储图(邻接表的链式前向星)。遍历时采用的方式类似于广度优先搜索法，使用动态逼近的形式，在遍历时如果一条边的路径最小，需要松弛，并且边的终点没有在队列中，就将该边的终点入队列，直到队列空为止，算法的平均时间复杂度为O(km)，k为所有顶点的平均入队列次数，所以说spfa算法在求最短路径时不稳定。
判断有无负环：如果一个点入队列次数超过N次，则为存在负环。

#define MAX 200100
#define MAX_VAL 99999999

struct edge
{
	int to; //边的终点 
	int val;//边的权值 
	int next;//上一条相同起点的边的编号 
}e[MAX];//e[i] 边的起点 i

int m;//边的数目 
int n;//顶点数目 
int head[MAX]; //表示以i为起点的边的编号 
int dis[MAX]; //表示1号点到i号点的距离

//边的添加 
void add(int from,int to,int val,int len)
{
	e[len].to = to;
	e[len].val = val;
	e[len].next = head[from];//head[from] 表示上一条起点为from 的边 的编号 
	head[from] = len;//添加这条边后，最新的以from为起点的边的编号是len 
}

//初始化路径数组的值，不能使用memset 
void Init(int* a,int len,int val)
{
	int i = 0;
	for(i = 0; i <= len; i++)
	{
		a[i] = val;
	}
}

void spfa()
{
	int s;
	queue<int>q;
	Init(dis,n,MAX_VAL);
	int visit[MAX];//查看该边是否在队列中 0-->不在  1-->在 
	int judge[MAX];//判断有无负环 
	memset(judge,0,sizeof(judge));
	memset(visit,0,sizeof(visit));
	dis[1] = 0;//初始化起点到起点的路径为0 
	q.push(1);
	visit[1] = 1;
	while(!q.empty())
	{
		int from = q.front();//得到队头的需要判断的边的起点 
		q.pop();
		visit[from] = 0;
		int i = 0;
		//遍历该起点可以到达的所有边 
		for(i = head[from];i != -1; i = e[i].next)
		{
			int to = e[i].to;
			//进行以from为起点的所有路径的松弛 
			if(dis[to] > dis[from] + e[i].val)
			{
				dis[to] = dis[from] + e[i].val;
				//如果成功松弛之后，把不在队列中的边加入队列中 
				if(visit[to] == 0)
				{
					q.push(to);
					visit[to] = 1;
					judge[to]++;
					if(judge[to] > n)
					{
						printf("存在负环\n");
						return ;
					}
				}
			}
		}
	}
}

spfa的两种优化思路

SLF ：假如从源点到要入队的节点的距离为 j，而从源点到队列队头节点的距离为 i ，要是j < i ，就把该节点插入队首。
LLL ：设从源点到队列队头节点的距离为 i ，队列中所有节点的最短路径平均值为dis，如果dis < i，就把i插入到队尾，查找下一元素，直到找到某一个i 使得 dis >= i，就将i 出队进行松弛操作。

来源：CSDN

作者：Windy _ X

链接：https://blog.csdn.net/duchenlong/article/details/104010441

标签

最短路径