最短路径问题【Bellman-Ford】

Time Limit:10000MS Memory Limit:65536K
Total Submit:619 Accepted:330
Case Time Limit:1000MS

---

Description
平面上有$n$个点$(N<=100)$，每个点的坐标均在$-10000~10000$之间。其中的一些点之间有连线。若有连线，则表示可从一个点到达另一个点，即两点间有通路，通路的距离为两点直线的距离。现在的任务是找出从一点到另一点之间的最短路径。

---

Input
输入文件$short.in$，共有$n+m+3$行，其中：
第一行为一个整数$n$。
第$2$行到第$n+1$行（共$n$行），每行的两个整数$x$和$y$，描述一个点的坐标(以一个空格隔开)。
第$n+2$行为一个整数$m$，表示图中的连线个数。
此后的$m$行，每行描述一条连线，由两个整数$I,j$组成，表示第$i$个点和第$j$个点之间有连线。
最后一行：两个整数$s$和$t$，分别表示源点和目标点。

Output
输出文件$short.out$仅一行，一个实数(保留两位小数)，表示从$S$到$T$的最短路径的长度。

---

Sample Input
5
0 0
2 0
2 2
0 2
3 1
5
1 2
1 3
1 4
2 5
3 5
1 5

Sample Output
3.41

---

解题思路

算法解析： 同样是用来计算从一个点到其他所有点的最短路径的算法，也是一种单源最短路径算法。
能够处理存在负边权的情况，但无法处理存在负权回路的情况。。。

$Bellman-Ford$算法的思想很简单。一开始认为起点是白点$(dis[1]=0)$，每一次都枚举所有的边，必然会有一些边，连接着白点和蓝点。因此每次都能用所有的白点去修改所有的蓝点，每次循环也必然会有至少一个蓝点变成白点。

图解走起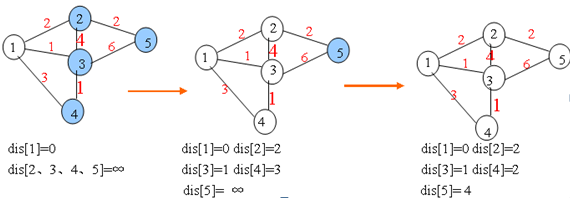

在上面这个简单的模拟中能看到白点的“蔓延”情况。

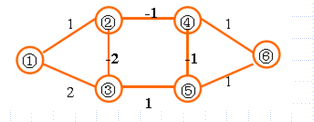
上图中$②-④-⑤-③-②$这条回路的边权之和为$-3$。在有负权回路的情况下无法求出最短路径，但$Bellman-Ford$算法可以在有负权回路的情况下输出错误提示。

---

代码

#include<iostream>
#include<cstring>
#include<iomanip>
#include<cmath>
using namespace std;
int n,m,s,t,a[5000][3];
double f[2000],dis[2000],minn;
int x[2000],y[2000];   
int k=0;
int main(){
	cin>>n;
	for(int i=1;i<=n;i++)
		cin>>a[i][1]>>a[i][2];
	cin>>m;                
	for(int i=1;i<=m;i++)
	{
		cin>>x[i]>>y[i];
		f[i]=sqrt(pow(double(a[x[i]][1]-a[y[i]][1]),2)+pow(double(a[x[i]][2]-a[y[i]][2]),2));//记录边权，计算两点间距离。。。
	}
	cin>>s>>t;
	 memset(dis,0X7f,sizeof(dis));
	 dis[s]=0;
	for(int i=1;i<=n;i++)//查找可以更新的点
	{
		k=0; 
		int t=0;//记录是否松驰
		for(int j=1;j<=m;j++)
		{
			
			if(dis[x[j]]+f[j]<dis[y[j]])
			{
				dis[y[j]]=dis[x[j]]+f[j];
				t=1;
			}
			if(dis[y[j]]+f[j]<dis[x[j]])
			{
				dis[x[j]]=dis[y[j]]+f[j];
				t=1;
			}
		}
		if(!t)//如果有对所有边没有松驰，则不需要进行操作
		break;
	}
	cout<<fixed<<setprecision(2)<<dis[t];
}

来源：CSDN

作者：SSL KJ

链接：https://blog.csdn.net/kejin2019/article/details/104005039