[数据结构]-04顺序表和链表

顺序表

按照顺序存储方式存储的线性表称为顺序表。

什么是有序顺序表？
若顺序表中的元素按其值有序，则称其为有序顺序表。

顺序表的插入

设顺序表 $A$ 的长度为 $n$，将字段值为 $item$ 的元素插入到第 $i$ 个位置，插入步骤如下：

• 保证顺序表存储空间未满，并且插入位置合法
• 将第 $i$ 个位置元素及其之后的所有元素后移一个位置
• 插入成功后，线性表长度变为 $n+1$

顺序表的删除

设顺序表 $A$ 的长度为 $n$，删除第 $i$ 个位置的元素，删除步骤如下：

• 保证删除位置合服性
• 将第 $i$ 个位置之后的所有元素前移一个位置
• 删除成功后，线性表长度变为 $n-1$

顺序表总结

• 特点：存储地址连续，数据元素存储依次存放；数据元素类型相同，数据元素可随机存取
• 优点：存储空间的利用率高，存取速度快，适用于存取需求多的线性表
• 缺点：静态存储形式，数据元素的个数不能自由扩充 (受存储空间的限制)；在插入、删除某个元素时，需要移动大量元素

单链表

结点只有一个指针域的链表成为单链表。
数据域 $data$ 存放该结点的数据域的值，指针域 $next$ 存放该结点的后继结点的地址信息。

什么是空链表？

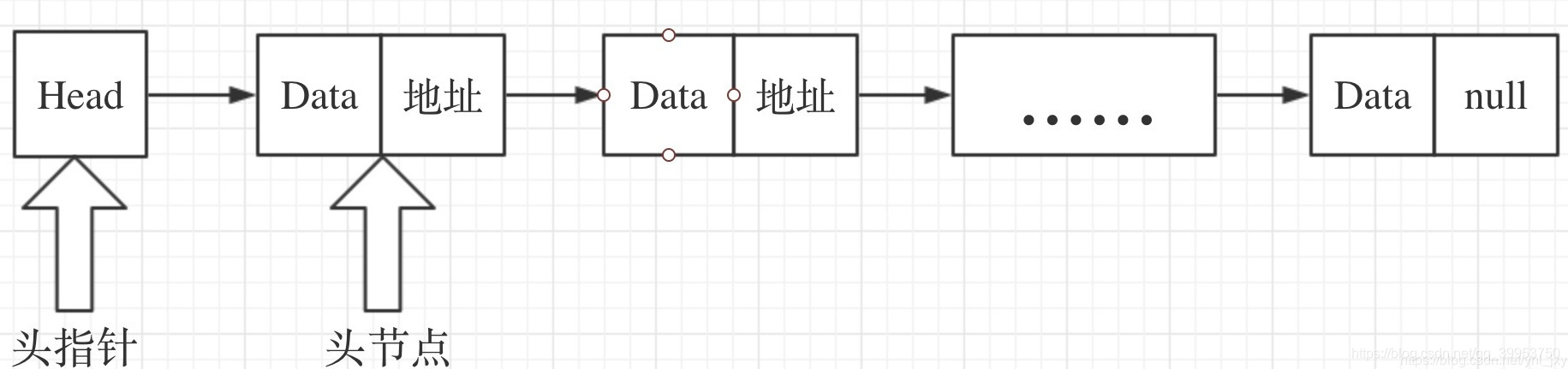
若表中只有头结点，则链表长度为 0，此时称其为空链表。

单链表的指针之间关系：
若 $p$ 为指向单链表第 $i$ 个结点的指针，则可以知道：

• $p.next$ 指向第 $i+1$ 个结点
• $p.data$ 为 $i$ 个结点的数据域
• $p.next.data$ 为 $i+1$ 个结点的数据域

通过头指针进入单链表，根据每个结点的指针域可以循环遍历整个链表。

单链表中获取元素

获取单链表第 $i$ 个数据步骤如下：

• 声明一个结点 $p$ 指向单链表的第一个结点，初始化 $j$ 从 1 开始；
• 当 $j<i$ 时遍历链表，让 $p$ 的指针向后移动，不断指向下一个结点，$j$ 累加 1；
• 若到单链表末尾 $p$ 为空，则说明第 $i$ 元素不存在；
• 否则查找成功，返回结点 $p$ 的数据。

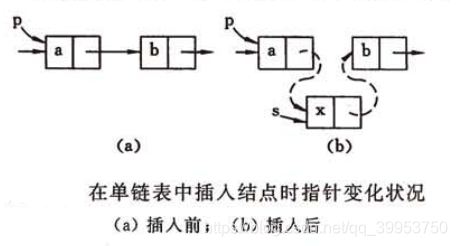
单链表的插入

将结点 $x$ 插入到单链表中的指定位置，若指针 $p$ 指向 $x$ 插入位置的前一个结点，插入步骤如下：

• 将 $x$ 结点的指针指向 $p$ 的后继结点： $x.next=p.next$
• 将 $p$ 的指针指向 $x$ 结点： $p.next=x$

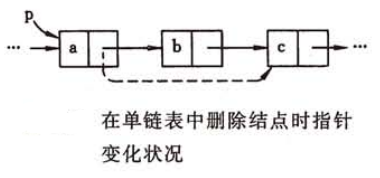
单链表的删除

删除单链表中的 $x$ 结点，若指针 $p$ 指向 $x$ 结点的前一个结点，删除步骤如下：

• 将 $p$ 的指针指向 $x$ 的后继结点：$p.next=p.next.next$
• 释放结点 $x$

#### 单链表的时间复杂度 - 单链表查询元素的最好时间复杂度为 $O(1)$，最坏时间复杂度为 $O(n)$，平均复杂度为 $O(n)$。 - 单链表的插入删除是先遍历链表，找到对应位置后进行插入和删除操作，整体的时间复杂度为 $O(n)$。

单链表和顺序表的比较

存储分配方式：

• 顺序表采用顺序存储方式，用一段连续的存储单元一次存储线性表中的数据元素
• 单链表采用链式存储方式，用一组任意的存储单元存放单链表中的元素

时间复杂度：

• 查找：顺序表的时间复杂度为 $O(1)$；单链表的时间复杂度为 $O(n)$。
• 插入和删除：顺序表平均移动表长一半的元素，时间复杂度为 $O(n)$；单链表在查找到某位置的指针后，插入和删除的时间复杂度为 $O(1)$。

空间性能：

• 线性表需要预先分配存储空间，若初始化时存储空间过大，容易造成浪费；若空间过小，容易引起数据的上溢。
• 单链表不需要预先分配存储空间，只要有空间就可以进行操作，单链表中的元素个数不受限制。

结论：

• 若线性表需要频繁查找，且插入删除操作较少，宜采用顺序表存储；
• 若线性表需要频繁进行插入和删除时，宜采用单链表存储。
• 当线性表中的元素个数变化较大或根本无法预知其变化时，宜采用单链表存储；
• 若能预知线性表的大致长度，宜采用顺序表存储。

应用实例

• 求单链表中有效结点个数
• 查找单链表中的倒数第 k 个结点
• 查找单链表中的倒数第 k 个结点，要求只能遍历一次链表
• 查找单链表的中间节点，要求只能遍历一次链表
• 单链表的逆序打印
• 逆置/反转单链表
• 单链表排序（冒泡排序&快速排序）
• 两个有序单链表进行合并，合并后依然有序
• 单链表实现约瑟夫环

循环链表

当单链表最后一个结点的指针域指向头结点时形成环状的链表称为循环链表。

什么是空循环链表？
当循环链表只包含一个头指针指向的头结点，其指针域存放指向自身的指针，称为空循环链表

循环链表与单链表的异同：

• 循环链表可以从任意位置访问任意结点；单链表只能访问任一结点之后的结点。
• 链表遍历的终止条件：结点的指针是否指向头指针；单链表遍历的终止条件：结点的指针是否为空。
• 循环链表可以获取前驱结点(遍历整个链表)；单链表无法获取前驱结点。
• 循环链表的插入和删除与单链表类似。

应用实例

• 约瑟夫问题
  • 设编号为 1,2,3,4…n 的 n 个人围坐一圈，约定编号为 k 的人从 1 开始报数，数到 m 的人出列，他的下一位又从 1 开始报数，数到 m 的人又出列，以此类推，直到所有人都出列，输出一个出列编号序列。

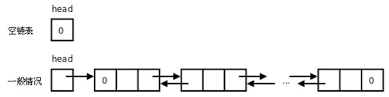
双向链表

结点由数据域( $data$ )、左指针域( $prior$ )、右指针域( $next$ )组成的链表称为双向链表。
左指针域和右指针域分别存放结点左右相邻结点的地址信息。

链表中的头结点的左指针和尾结点的右指针均为 $null$。

什么是双向循环链表？
在双向链表的基础上，头结点的左指针指向链表的位结点，尾结点的右指针指向头结点，这样的链表称为双向循环链表。

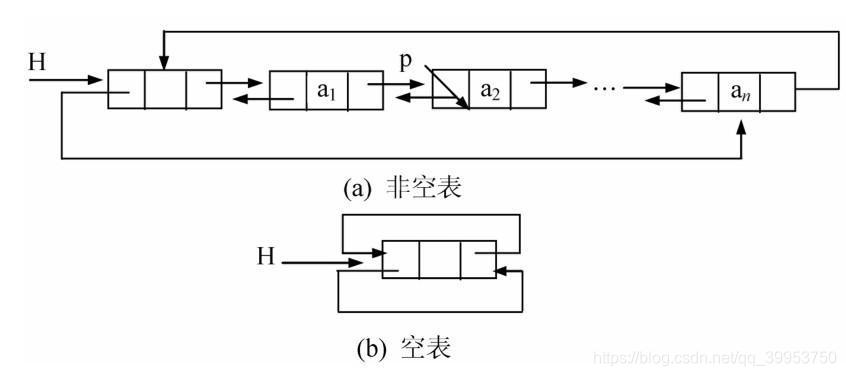
双向链表的指针之间关系：
若 $p$ 为指向第 $i$ 个结点的指针，则可以知道：

• $p.next$ 指向第 $i+1$ 个结点
• $p.prior$ 指向第 $i-1$ 个结点
• $p.prior.next=p.next.prior=p$

通过头指针进入双向循环链表，每个结点可以便利的访问其前驱结点和后继结点。

双向链表的插入

将结点 $x$ 插入到双向循环链表的指定位置，若指针 $p$ 指向 $x$ 插入位置的后一个结点，插入步骤如下：

• $x$ 结点的左指针指向 $p$ 的前驱结点： $x.prior=p.prior$
• $x$ 结点的右指针指向 $p$ 所在结点： $x.next=p$
• $p$ 的前驱结点的右指针指向 $x$ 结点： $p.prior.next=x$
• $p$ 的左指针指向 $x$ 结点： $p.prior=x$

双向链表的删除

删除双向循环链表的结点 $x$，若指针 $p$ 指向 $x$ 结点，删除步骤如下：

• $p$ 的后继结点的左指针指向 $p$ 的前驱结点： $p.next.prior=p.prior$
• $p$ 的前驱结点的右指针指向 $p$ 的后继结点： $p.prior.next=p.next$
• 指针 $p$ 的前驱结点的右指针指向 $x$ 结点： $p.prior.next=x$
• 指针 $p$ 的左指针指向 $x$ 结点： $p.prior=x$

链式存储总结

链式存储的优点：

• 结点空间可以动态申请和释放
• 数据元素的逻辑次序靠结点的指针来指示，插入和删除时不需要移动数据元素

链式存储结构的缺点：

• 存储密度小，每个结点的指针域需额外占用存储空间，当每个结点的数据域所占字节不多时，指针域所占存储空间的比重很大。

参考

• 《数据结构(C语言版)》 严魏敏、吴伟民著
• 《数据结构(第3版)》 刘大有等著
• 《大话数据结构》 程杰著

来源：CSDN

作者：V_vista

链接：https://blog.csdn.net/qq_39953750/article/details/103895808