
引导案例
案例一:
分销系统的返利: 比如B是A的下线,C是B的下线,那么在分钱返利的时候A可以分B,C的钱,这时候我们是不是就要分别找B,C的最后上级。这个问题我们一般怎么来解决呢?
C–>B–>A
案例二: .斐波那契数列:
1 1 2 3 5 8 13 21 ......
有什么特点?
从第三个数开始 就等于前面两个数相加;
数论思想:利用数学公式或者定理或者规律求解问题;
算法思想中最难的点:递归+动态规划
树论中(比如二叉树,红黑树)和递归密不可分,所以递归一定要弄明白了。
递归的定义
递归算法是一种直接或者间接调用自身函数或者方法的算法。
通俗来说,递归算法的实质是把问题分解成规模缩小的同类问题的子问题,然后递归调用方法来表示问题的解。
举个生活中的例子
比如我们在某窗口排队人太多了,我不知道我排在第几个,那么我就问我前面的人排第几个, 因为知道他排第几我就知道我是第几了。但前面的人也不知道自己排第几那怎么办呢?他也可以继续往前面问,直到问到第一个人,然后从第一个人一直传到我这里 我就很清楚的知道我是第几了。
以上这个场景就是一个典型的递归。我们在这个过程中大家有没有发现一个规律那么就是会 有一个问的过程,问到第一个后有一个回来的过程吧。这就是递(问)加归(回)。
那么这个过程我们是不是可以用一个数学公式来求解呢?那这个数学公式又是什么?
f(n)=f(n-1)+1
- f(n):表示我的位置
- f(n-1):表示我前面的那个人;
说白了 一个一个往前问 就是自己调用自己,完成这个功能。
推导出公式: f(n) = f(n-1) + f(n-2)
什么样的问题可以用递归算法来解决
需要满足的条件才可以用递归来解决?
(1)一个问题的解可以分解为几个子问题的解:
子问题,我们通过分治的思想可以把一个数据规模大的问题,分解为很多小的问题。
我们可以把刚刚那个问前面的那个人看为子问题。大化小
(2)这个问题与分解之后的子问题,求解思路完全一样:
(3)一定有一个最后确定的答案,即递归的终止条件。
刚刚那个问题就是第一个人。第一个人是肯定知道自己排第几吧即n=1的时候,如果没有这个特性那么我们这个递归就会出现死循环,最后程序就是栈溢出;StackOverflowError
递归并不是马上返回,而是一层一层的保存在Stack里边,满足结束条件后才一层一层的返回.
递归如何实现以及包含的算法思
递归,回溯(归的过程);
递归的关键相信大家已经知道了就是要(1)求出这个递归公式,(2)找到终止条件。
现在我们可以回到课堂前跟大家讲的那个斐波那契数列数列:1 1 2 3 5 8 13 这个的数列我们称之为斐波那契数列
按照我们说的 两个点 ,来分析一下:
求解公式:f(n)=f(n-1)+f(n-2)
终止条件:n<=2 也就是f(n)=1
斐波那契数列代码实现
分析一下,给定一个值n , 输出 n个数字组成一个斐波那契数列
从n开始,一直往前递归,直到符合终止条件即可。
public class Fibonacc {
public static int fab(int n){
if(n <=2 ) return 1; // 终止条件
return fab(n-1) + fab(n-2); // 递归公式
}
public static void main(String[] args) {
for (int i = 1; i <= 10; i++) {
System.out.println(i + ":" + fab(i));
}
}
}
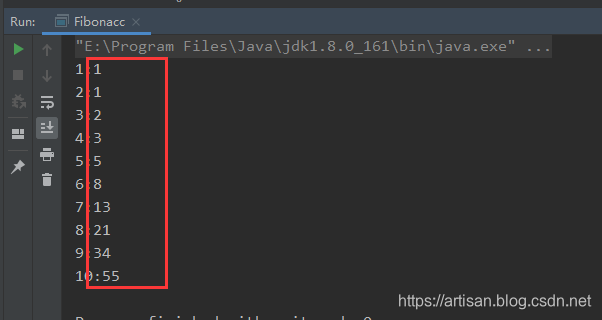
递归的时间复杂度(2^n)和空间复杂度(2^n)
代码实现了,我们来分析下 递归的复杂度
以斐波那契数列为例为分析递归树:
f(n)=f(n-1)+f(n-2)

图一画,一目了然 , 时间复杂度 2^n
空间复杂度的话,递归并不是马上返回,而是一层一层的保存在Stack里边,因为还有一个 归的过程,满足结束条件后才一层一层的返回. 空间复杂度自然也是 2^n
来源:CSDN
作者:小小工匠
链接:https://blog.csdn.net/yangshangwei/article/details/103943043