11-接下来如何做

1.树

在前面的二分查找示例中，每当用户登陆Facebook，Facebook都必须在一个庞大的数组中查找，核实其中是否包含指定的用户名。在这种数组中查找，最快的方式是二分查找，但问题是每当有新用户注册时，都必须将其用户名插入该数组并重新排序，因为二分查找仅在数组有序时才管用。如果能将用户名插入到数组的正确位置就好了，这样就无需在插入后再排序。为此，有人设计了一种名为二叉查找树的数据结构。
对于其中的每个节点，左子节点的值都比它小，而右子节点的值都比它大。

假设要查找Maggie，首先检查根节点。Maggie排在David的后面，因此你往右找。Maggie排在Manning前面，因此你往前找。

二叉查找树用时为O(log₂n)几乎与二分查找一样，但在最糟的情况下所需时间为O(n)；而在有序数组中查找时，即便是在最糟情况下所需的时间也只有O(log₂n)，但是二叉查找树的插入和删除操作的速度要快得多。

操作	有序数组	二叉查找树
查找	O(log2n)	O(log2n)
插入	O(n)	O(log2n)
删除	O(n)	O(log2n)

二叉查找树的缺点：不能随机访问，例如给我第5个元素。在二叉查找树处于平衡状态时平均访问时间也为O(log₂n)。
假设二叉查找树像下面这样处于不平衡状态。

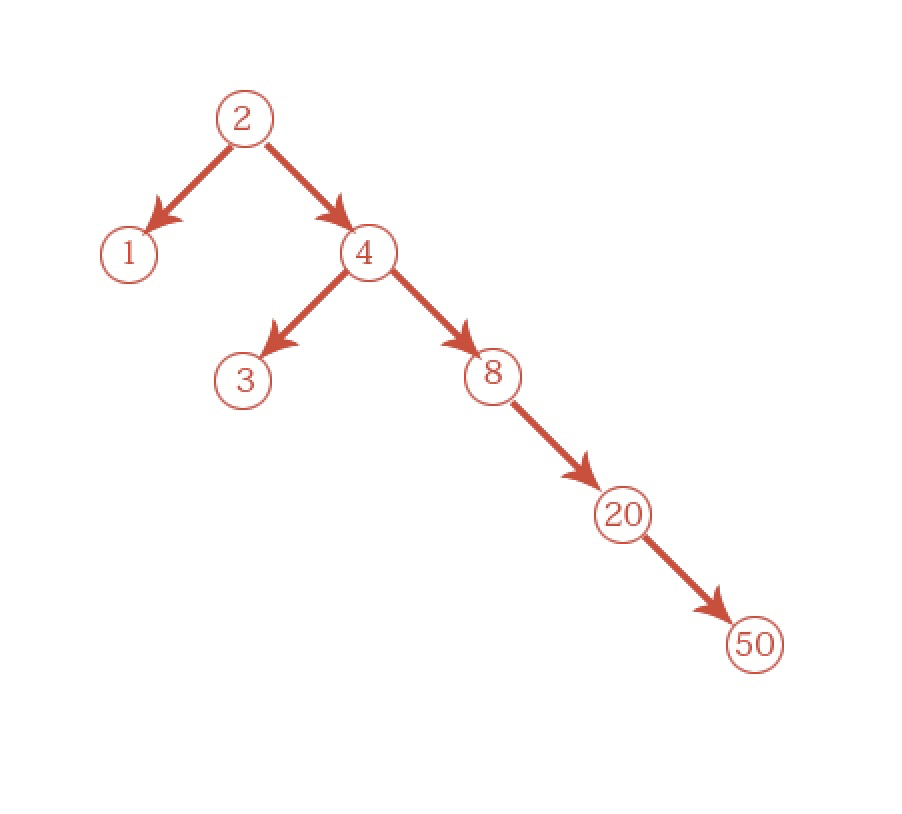
注意，这棵树是向右倾斜的，因此性能不佳。也有一些处于平衡状态的特殊二叉查找树，如红黑树。

场景：在什么情况下使用二叉查找树呢？B树是一种特殊的二叉树，数据库常用它来存储数据。
高级数据结构：B树，红黑树，堆，伸展树。

2.反向索引

假设有3个网页，我们根据这些内容创建一个散列表。这个散列表的键为单词，值为包含指定单词的页面。

键（指定单词）	值（包含指定单词的页面）
Hi	A,B
Adit	B
We	C
Go	C

搜索引擎发现页面A和B包含Hi，因此将这些页面作为搜索结果呈现给用户。现在假设用户搜索There，搜索引擎将返回A和C。
这是一种很有用的数据结构：一个散列表，将单词映射到包含它的页面。这种数据结果成为反向索引，常用语创建搜索引擎。

3.傅立叶变换

https://betterexplained.com/articles/an-interactive-guide-to-the-fourier-transform/中对于傅立叶变换的解释：
What does the Fourier Transform do? Given a smoothie, it finds the recipe.给它一杯冰沙，它能告诉你其中包含哪些成分。或者给定一首歌曲，傅立叶变换能够将其中的各种频率分离出来。
应用：将歌曲分解成不同的频率，就可强化你关心的部分，如强化低音并隐藏高音。傅立叶变换非常适合用于处理信号，可使用它来压缩音乐。为此，首先需要将音频文件分解为音符。傅立叶变换能够准确的指出各个音符对整个歌曲的贡献，让你能够将不重要的音符删除。这就是mp3的工作远离。jpg也是如此。
傅立叶变换还被用来预测地址和DNA分析。

4.并行算法

接下来的三个主题都与可扩展性和海量数据处理相关。目前电脑基本使用的是多核处理器。为提高算法的速度，你需要让它们能够在多个内核中并行的执行。
在最佳情况下，排序算法的速度大致为O(log₂n)。对数组进行排序时，除非使用并行算法，否则运行时间不可能为O(n)！对数组进行排序时，快速排序的并行版本所需的时间为O(n)。
并行算法设计起来很难，要确保它们能够正确的工作并实现期望的速度提升也很难。还有速度的提升并非线性的。即便电脑硬件条件增加1倍，算法的速度也不可能提高1倍。原因：

• 1.并行性管理开销。假设你要对一个包含1000个元素的数组进行排序，如何在两个内核之间分配这项任务呢？如果让每个内核对其中500个元素进行排序，再将两个排好序的数组合并成一个有序数组，那么合并也是需要时间的。
• 2.负载均衡。假设你需要完成10个任务。电脑为双核，每个内核执行5个任务。但分配给A的任务都很容易，10秒钟就完成了；分配给B的任务都很难，1分钟才完成。这意味着有那么50秒，内核B在疯狂运行，而内核A却闲得很。你如何均匀的分配任务，让两个内核一样忙呢？

要改善性能和可扩展性，并行算法可能是不错的选择。

5.MapReduce

有一种特殊的并行算法日益流行，他就是分布式算法。在并行算法只需2-4个内核时，完全可以在笔记本上运行它，但如果需要数百个内核呢？在这种情况下，可让算法在多台计算机上运行。MapReduce是一种流行的分布式算法，可通过流行的开源工具Apache Hadoop来使用它。

5.1分布式算法为何很有用

假设你有一个数据库表，包含数十亿乃至数万亿条数据，需要对其执行复杂的SQL查询。在这种情况下，你不能使用MySQL，因为数据表的行数超过数十亿后，它处理起来将很吃力。相反，你需要通过Hadoop来使用MapReduce。

又假设你需要处理一个很长的清单，其中包含100万个职位，而每个职位处理起来需要10秒。如果使用一台计算机来处理，将耗时数月。如果使用100台计算机来处理，可能几天就能完工。

5.2映射函数

映射函数很简单，它接收一个数组，并对其中的每个元素执行同样的处理。例如将每个元素翻倍。

arr=[1,2,3,4,5]
arr2 = map(lambda x:2*x,arr)
print(list(arr2))    #[2, 4, 6, 8, 10]

你有一个URL清单，需要下载每个URL指向的页面并将这些内容存储在数组arr2中。对于每个URL，处理起来都可能需要几秒钟。如果总共有1000个URL，可能耗时几个小时。如果有100台计算机，而map能够自动将工作分配给这些计算机去完成就好了。这样就可同时下载100个页面，下载速度将快得多。这就是MapReduce中映射部分基本的理念。

5.3归并函数

归并函数可能令人迷惑，其理念是将很多项归并为一项。映射是将一个数组转换为另一个数组。
而归并是将一个数组转换为一个元素。

arr=[1,2,3,4,5]
arr2 = reduce(lambda x,y:x+y,arr)
print(arr2)

MapReduce使用这两个简单概念在多台计算机上执行数据查询。数据集很大，包含数十亿行时，使用MapReduce只需几分钟就可获得查询结果，而传统数据库可能要耗费数小时。

6.布隆过滤器和HyperLogLog

6.1 布隆过滤器

6.2 HyperLogLog

7.SHA算法

7.1 比较文件

7.2 检查密码

8.局部敏感的散列算法

9.Diffie-Hellman密钥交换

10.线性规划

来源：https://www.cnblogs.com/csj2018/p/12181771.html