Leetcode141. 环形链表

题目：
给定一个链表，判断链表中是否有环。
为了表示给定链表中的环，我们使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。如果 pos 是 -1，则在该链表中没有环。
示例 1：
输入：head = [3,2,0,-4], pos = 1
输出：true
解释：链表中有一个环，其尾部连接到第二个节点。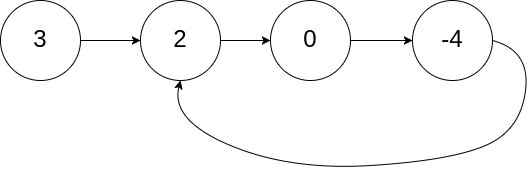

题解：
方案一：hash表
我们遍历所有结点并在哈希表中存储每个结点的引用（或内存地址）。如果当前结点为空结点 null（即已检测到链表尾部的下一个结点），那么我们已经遍历完整个链表，并且该链表不是环形链表。如果当前结点的引用已经存在于哈希表中，那么返回 true（即该链表为环形链表）。

时间复杂度： $O(n)$ ，对于含有 $n$ 个元素的链表，我们访问每个元素最多一次。添加一个结点到哈希表中只需要花费 $O(1)$ 的时间。
空间复杂度： $O(n)$ ，空间取决于添加到哈希表中的元素数目，最多可以添加 $n$ 个元素。

方案二：双指针
通过使用具有不同速度的快、慢两个指针遍历链表，空间复杂度可以被降低至 $O(1)$ 。慢指针每次移动一步，而快指针每次移动两步。
想象成两名运动员以不同的速度在环形跑道上跑步，终究会相遇（扣圈）

时间复杂度： $O(n)$ ，让我们将 $n$ 设为链表中结点的总数。为了分析时间复杂度，我们分别考虑下面两种情况。

链表中不存在环：
快指针将会首先到达尾部，其时间取决于列表的长度，也就是 $O(n)$ 。
链表中存在环：
我们将慢指针的移动过程划分为两个阶段：非环部分与环形部分：
慢指针在走完非环部分阶段后将进入环形部分：此时，快指针已经进入环中迭代次数 =非环部分长度 $= N$
两个指针都在环形区域中：考虑两个在环形赛道上的运动员 - 快跑者每次移动两步而慢跑者每次只移动一步。其速度的差值为 1，因此需要经过 $\dfrac{\text{二者之间距离}}{\text{速度差值}}$ 次循环后，快跑者可以追上慢跑者。这个距离几乎就是 “ $\text{环形部分长度 K}$ ” 且速度差值为 1，我们得出这样的结论 $\text{迭代次数} = \text{近似于}"\text{环形部分长度 K}"$ .
因此，在最糟糕的情形下，时间复杂度为 $O(N+K)$ ，也就是 $O(n)$ 。

空间复杂度： $O(1)$ ，我们只使用了慢指针和快指针两个结点，所以空间复杂度为 $O(1)$ 。

scala代码如下：
hash表

def hasCycle(head: ListNode): Boolean = {
    var head1 = head
    val nodesSeen = new java.util.HashSet[ListNode]()
    var result = false
    var flag = true
    while (head1 != null && flag) {
      if (nodesSeen.contains(head1)) {
        flag = false
        result = true
      } else {
        nodesSeen.add(head1)
      }
      head1 = head1.next
    }
    result
  }

双指针法：

 /**
    * 双指针
    *
    * @param head
    * @return
    */
  def hasCycle2(head: ListNode): Boolean = {
    var result = true
    var flag = true
    if (head == null || head.next == null) {
      result = false
      flag = false
    }
    var slow = head
    var fast = head.next
    while (slow != fast && flag) {
      if (fast == null || fast.next == null) {
        result = false
        flag = false
      } else {
        slow = slow.next
        fast = fast.next.next
      }
    }
    result
  }

来源：CSDN

作者：会流泪de鱼

链接：https://blog.csdn.net/sunhaiting666/article/details/103804625

标签

链表

指针

时间复杂度