最小生成树
最小生成树的算法包括Prim算法和Kruskal算法。
在用Kruscal算法的时候会用到并查集。
完整代码可直接翻到最后~
首先咱们先介绍比较容易理解也是最先会想到的一个算法,Prim算法。
Prim
Prim算法的时间复杂度为O(n^2)。
Prim算法的思想就是从图中任意一点选择为始点,然后开始搜索可以从这个点到达其他点的最短距离。其实这个思想和Dijstra算法很相似。
不同之处在于,Dijstra算法计算的是点到点最短距离,Prim算法是把所有点连通起来权值最小。
实质上也就是,Dijstra算法在把某个点加入到集合中时,它的算法仅仅只是把这个点当做一个跳板,内部点与点之间还是存在距离(得到了某个人却没有得到它的心)。而Prim算法则是把这个点合在了一起,也就是在加入某个点之后,就可以把这些点看成一个点,集合内部没有距离(得到某个人并且得到了它的心)。
看例子(从0开始):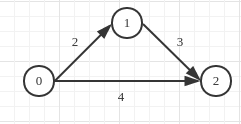
用Dijstra算法
首先0,然后0->1, 最后0->2。
用Prim算法
首先0,然后0->1,最后1->2。
所以这两个算法的区别就是在于0->1这个距离在后续中考虑存在与否。更一般的就是被添加到集合中的点与点之间的距离是否还存在。
好的,请看算法核心代码
void Primnew () {
int V[N]; //V[] 记录节点的前驱
int dis[N];//记录当前到各个节点的权值
//初始化,起点为3,权值取自于矩阵
for(int i = 0; i < N; ++i) {
dis[i] = Edge[3][i];
V[i] = 3;
}
V[3] = 0;
//迭代寻找N-1条边
for(int i = 0; i < N-1; ++i) {
int shorter = M;
int e = 0;
//找到当前到其他点的 最短距离 和 其节点
for(int j = 0; j < N; ++j) {
if (shorter > dis[j] && dis[j] != 0) {
shorter = dis[j];
e = j;
}
}
//与Dijstra的不同之处
//节点找到后,权值更新为0
dis[e] = 0;
//加入节点后,更新当前路径
for(int i = 0; i < N; ++i) {
if(dis[i] > Edge[e][i]) {
dis[i] = Edge[e][i];
V[i] = e;
}
}
}
}
好的,Prim算法结束。接下来就是Kruskal算法。
在介绍Kruskal算法之前,先了解什么是并查集。
并查集
并查集的最简单的定义,朋友的朋友就是朋友。
通过与树结合,也可以这么说,祖辈的祖辈就是祖辈。
看例子:
阿珍和阿强,他们两个人是大学同学。
他们两个人的族谱图(为了简单,只画到父辈)为: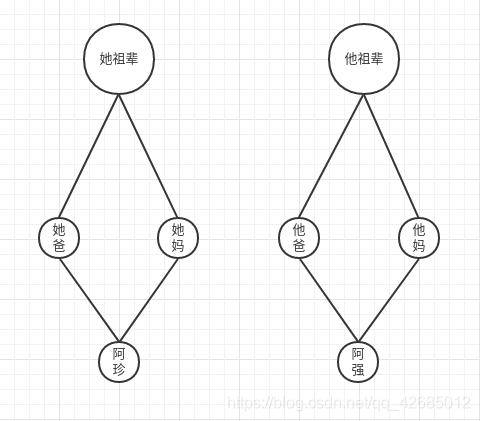
在一风雨交加晚,电光雷鸣时,阿珍爱上了阿强。在恋爱期间,两个人相约厮守到老。
毕业后见家长,为了避免近亲,两个人在结婚前需要查自家的族谱图。若祖上有关系,也只能是有情人终成兄妹。但是好在最后结果为两人祖上N代毫无干系。
可以结婚。
婚后,阿珍和阿强的族谱图变成了: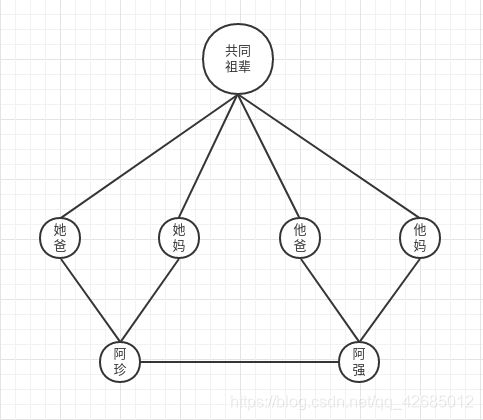
至此,我们已经了解了并查集的概念,和并查集的两个操作。
并查集的概念
把两个毫无关系的集合通过各自集合中的某个点,当这两个点存在关系时,则表面可以把这两个集合合并成一个集合了。
两个操作
查询:查询自己的祖辈,是否是和对方的祖辈相同
合并:当祖辈不同时,两个点又存在关系,就可以把祖辈合二为一
当了解并查集之后,咱们就可以来看Kruskal算法了。
Kruskal
Kruskal算法的时间复杂度为O(n*m)。
Kruskal算法的思想就是每次遍历所有的边,选择权值最小,并且路径两端的节点属于不同的集合的路径。每次遍历都可以筛选出一条路径,并且合并两个集合。所以只需要遍历N-1次,即可完成搜索。
在了解完并查集之后,Kruskal算法其实也就很简单明了。
请看代码:
//寻找集合的祖辈
int found(int x) {
if(anc[x] == x) return x;
else anc[x] = found(anc[x]);
return anc[x];
}
//合并祖辈
void unite(int x, int y) {
int px = found(x);
int py = found(y);
if(px == py) return;
anc[px] = py;
}
void Kruskal () {
for(int k = 0; k < N - 1; ++k) {
int shorter = M;
int s, e;
for(int i = 0; i < N; ++i) {
for(int j = i; j < N; ++j) {
if(shorter > Edge[i][j] && found(i) != found(j)) {
s = i;
e = j;
shorter = Edge[i][j];
}
}
}
unite(s, e);
}
}
Prim完整代码
#include <iostream>
#include <vector>
using namespace std;
#define N 7
#define M 999999
char Ch[N] = {'A', 'B', 'C', 'D', 'E', 'F', 'G'};
int Edge[N][N] = {0, 7, M, 5, M, M, M,
7, 0, 8, 9, 7, M, M,
M, 8, 0, M, 5, M, M,
5, 9, M, 0, 15, 6, M,
M, 7, 5, 15, 0, 8, 9,
M, M, M, 6, 8, 0, 11,
M, M, M, M, 9, 11, 0};
struct Edg {
char start, end;
int weight;
};
void Prim () {
int V[N]; //V[] 记录节点的前驱
Edg E[N-1];
int dis[N];//记录当前到各个节点的权值
//初始化,起点为3,权值取自于矩阵
for(int i = 0; i < N; ++i) {
dis[i] = Edge[3][i];
V[i] = 3;
}
V[3] = 0;
//迭代寻找N-1条边
for(int i = 0; i < N-1; ++i) {
int shorter = M;
int e = 0;
//找到当前到其他点的 最短距离 和 其节点
for(int j = 0; j < N; ++j) {
if (shorter > dis[j] && dis[j] != 0) {
shorter = dis[j];
e = j;
}
}
//节点找到后,权值更新为0
dis[e] = 0;
//记录树的父子以及权值
E[i].start = Ch[V[e]];
E[i].end = Ch[e];
E[i].weight = shorter;
//加入节点后,更新当前路径
for(int i = 0; i < N; ++i) {
if(dis[i] > Edge[e][i]) {
dis[i] = Edge[e][i];
V[i] = e;
}
}
}
for(int i = 0; i < N-1; ++i) {
cout << E[i].start << " -> " << E[i].end << " = "<< E[i].weight << endl;
}
}
int main() {
for(int i = 0; i < N; ++i) {
for(int j = 0; j < N; ++j)
cout << Edge[i][j] << "\t";
cout << "\n";
}
Prim();
return 0;
}
Kruskal完整代码
#include <iostream>
#include <vector>
using namespace std;
#define N 7
#define M 999999
char Ch[N] = {'A', 'B', 'C', 'D', 'E', 'F', 'G'};
int Edge[N][N] = {0, 7, M, 5, M, M, M,
7, 0, 8, 9, 7, M, M,
M, 8, 0, M, 5, M, M,
5, 9, M, 0, 15, 6, M,
M, 7, 5, 15, 0, 8, 9,
M, M, M, 6, 8, 0, 11,
M, M, M, M, 9, 11, 0};
struct Edg {
char start, end;
int weight;
};
int anc[N] = {0, 1, 2, 3, 4, 5, 6};
int found(int x) {
if(anc[x] == x) return x;
else anc[x] = found(anc[x]);
return anc[x];
}
void unite(int x, int y) {
int px = found(x);
int py = found(y);
if(px == py) return;
anc[px] = py;
}
void Kruskal () {
Edg E[N];
for(int k = 0; k < N - 1; ++k) {
int shorter = M;
int s, e;
for(int i = 0; i < N; ++i) {
for(int j = i; j < N; ++j) {
if(shorter > Edge[i][j] && found(i) != found(j)) {
s = i;
e = j;
shorter = Edge[i][j];
}
}
}
unite(s, e);
E[k].start = Ch[s];
E[k].end = Ch[e];
E[k].weight = shorter;
}
for(int i = 0; i < N-1; ++i) {
cout << E[i].start << " -> " << E[i].end << " = "<< E[i].weight << endl;
}
}
int main() {
for(int i = 0; i < N; ++i) {
for(int j = 0; j < N; ++j)
cout << Edge[i][j] << "\t";
cout << "\n";
}
Kruskal();
return 0;
}
来源:CSDN
作者:胖狗子修行之路
链接:https://blog.csdn.net/qq_42685012/article/details/103804967