python实现排序算法(三)
堆排序
堆排序(Heapsort)的基本思想:是指利用堆这种数据结构所设计的一种排序算法。堆积是一个近似完全二叉树的结构,并同时满足堆积的性质:即子节点的键值或索引总是小于(或者大于)它的父节点。
算法原理
堆排序基本思想是:
-
将初始待排序关键字序列(R1,R2…Rn)构建成大顶堆,此堆为初始的无序区。
-
将堆顶元素 R[1]与最后一个元素 R[n]交换,此时得到新的无序区(R1,R2,…Rn-1)和新的有序区(Rn),且满足 R[1,2…n-1]<=R[n]。
-
由于交换后新的堆顶 R[1]可能违反堆的性质,因此需要对当前无序区(R1,R2,…Rn-1)调整为新堆,然后再次将 R[1]与无序区最后一个元素交换,得到新的无序区(R1,R2…Rn-2)和新的有序区(Rn-1,Rn)。不断重复此过程直到有序区的元素个数为 n-1,则整个排序过程完成。
复杂度分析
-
最坏复杂度: 时间复杂度为 O(nlogn)
-
最好复杂度:时间复杂度在 O(nlogn)
-
平均复杂度: 时间复杂度为 O(nlogn)
算法实现
import random
def heap_sort(sequence):
def heap_adjust(parent):
#左孩子
child = 2 * parent + 1
#孩子的索引值小于堆的长度
while child < len(heap):
if child+1 < len(heap):
#右孩子大于左孩子
if heap[child + 1] > heap[child]:
child = child + 1
if heap[parent] >= heap[child]:
break
#父节点的值与孩子节点的值进行交换
heap[parent], heap[child] = heap[child], heap[parent]
#父亲的索引为孩纸的索引,孩子的索引为孩子的左孩子索引
parent, child = child, 2 * child + 1
#复制堆序列的值,初始序列列表
heap, sequence = sequence.copy(), []
#调整
for i in range(len(heap) // 2, -1, -1):
heap_adjust(i)
while len(heap) != 0:
#堆的首尾交换
heap[0], heap[-1] = heap[-1], heap[0]
#在序列0位置插入堆弹出的尾值
sequence.insert(0, heap.pop())
#调整堆
heap_adjust(0)
return sequence
if __name__ == '__main__':
sequence = [random.randint(1, 10000) for i in range(10)]
print(sequence)
print(heap_sort(sequence))
计数排序
计数排序(Counting Sort)不是基于比较的排序算法,其核心在于将输入的数据值转化为键存储在额外开辟的数组空间中。 作为一种线性时间复杂度的排序,计数排序要求输入的数据必须是有确定范围的整数。
算法原理
计数排序基本思想是:
-
根据待排序集合中最大元素和最小元素的差值范围,申请额外空间;
-
遍历待排序集合,将每一个元素出现的次数记录到元素值对应的额外空间内;
-
对额外空间内数据进行计算,得出每一个元素的正确位置;
-
将待排序集合每一个元素移动到计算得出的正确位置上。
复杂度分析
-
最坏复杂度: 时间复杂度为 O(n+k)
-
最好复杂度:时间复杂度在 O(n+k)
-
平均复杂度: 时间复杂度为 O(n+k)
演示示例
待排序集合:[3, -1, 2, 3, 1]
step 1:
序列中最大值为:max=3,最小值为:min=-1,根据序列中最大值和最小值的差值范围,可得申请额外空间大小为:max-min+1=5
step 2:
因为申请的额外空间足以将min 和max之间的所有元素记录,所以将待排序集合中每一个元素都记录到额外空间上,例如元素 3,对应的记录位置下标为:index=3-min=4,即最后一个位置;元素 -1,对应的记录位置下标为:index=-1-min=0,即第一个位置。
所有元素的出现次数和元素值记录如下,其中 times表示该元素出现的次数, value表示元素值: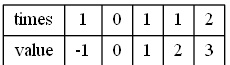
可以发现,计数排序的该过程,其实就是将待排序集合中的每个元素值本身大小作为下标,依次进行了存放。而记录的 times 次数,就是为了确定该元素值出现了几次。
step 3:
记录每个元素出现的次数,并对次数做计算,作用是当移动待排序集合元素到已排序集合中时,确保相同元素都被移动,且保持算法稳定性。因为额外空间中元素值是有序排列的,即额外空间的序列中每个元素,其元素的最终位置都是在前一个元素的后面,所以将其中每个元素的次数更新为加上前一个元素的次数和。例如元素 2 的最终位置在 元素 1 之后,而元素 1 只出现了 1 次,所以将元素 2 的times值更新为 3。

step 4:
根据额外空间已经确定的元素序列,移动待排序集合元素到已排序集合中。
参考链接:https://www.jianshu.com/p/86c2375246d7
算法实现
import random
def counting_sort(sequence):
#序列为空,返回
if sequence==[]:
return []
#序列的长度
sequence_len=len(sequence)
#序列中的最大值
sequence_max=max(sequence)
#序列中的最小值
sequence_min=min(sequence)
#计数数组的长度=最大值-最小值+1
counting_arr_length=sequence_max-sequence_min+1
#将计数数组中的值全部置0
counting_arr=[0]*counting_arr_length
#遍历序列
for number in sequence:
#计数数组当前值-最小值下标每访问一次加一,即相同的数,每访问一次加一,进行计数
counting_arr[number-sequence_min]+=1
for i in range(1,counting_arr_length):
#对所有得计数累加(从 C 中的第一个元素开始,每一项和前一项相加)
counting_arr[i]=counting_arr[i]+counting_arr[i-1]
#目标数组置0
ordered=[0]*sequence_len
#逆序遍历
for i in range(sequence_len-1,-1,-1):
#将每个元素 i 放在新数组的第 C(i)项,每放一个元素就将 C(i)减去 1。
ordered[counting_arr[sequence[i]-sequence_min]-1] = sequence[i]
counting_arr[sequence[i]-sequence_min]-=1
return ordered
if __name__ == '__main__':
sequence = [random.randint(1, 10) for i in range(10)]
print(sequence)
print(counting_sort(sequence))
桶排序
桶排序是计数排序的升级版。它利用了函数的映射关系,高效与否的关键就在于这个映射函数的确定。桶排序 (Bucket sort)的工作原理:假设输入数据服从均匀分布,将数据分到有限数量的桶里,每个桶再分别排序(有可能再使用别的排序算法或是以递归方式继续使用桶排序进行排)。
算法原理
计数排序基本思想是:
-
设置一个定量的数组当作空桶;
-
遍历输入数据,并且把数据一个一个放到对应的桶里去;
-
对每个不是空的桶进行排序;
-
从不是空的桶里把排好序的数据拼接起来。
复杂度分析
-
最坏复杂度: 时间复杂度为 O(n+k)
-
最好复杂度:时间复杂度在 O(n)
-
平均复杂度: 时间复杂度为 O(n)
算法实现
import math
import random
#默认桶的大小为5
DEFAULT_BUCKET_SIZE = 5
def insertion_sort(sequence):
#插入排序
for index in range(1, len(sequence)):
while(index > 0 and sequence[index-1] > sequence[index]):
sequence[index], sequence[index-1] = sequence[index-1], sequence[index]
index = index-1
return sequence
def bucket_sort(sequence, bucketSize=DEFAULT_BUCKET_SIZE):
if(len(sequence) == 0):
return []
#初始最大值最小值为序列首个元素
minValue = sequence[0]
maxValue = sequence[0]
for i in range(0, len(sequence)):
# 寻找最小值
if sequence[i] < minValue:
minValue = sequence[i]
# 寻找最大值
elif sequence[i] > maxValue:
maxValue = sequence[i]
# 桶的数目
bucketCount = math.floor((maxValue - minValue) / bucketSize) + 1
buckets = []
for i in range(0, bucketCount):
buckets.append([])
# 遍历数据,将数据依次放进桶中
for i in range(0, len(sequence)):
buckets[math.floor((sequence[i] - minValue) /
bucketSize)].append(sequence[i])
sortedArray = []
# 将每一个不是空的桶进行插入排序
for i in range(0, len(buckets)):
insertion_sort(buckets[i])
for j in range(0, len(buckets[i])):
sortedArray.append(buckets[i][j])
return sortedArray
if __name__ == '__main__':
sequence = [random.randint(1, 10000) for i in range(50)]
print(sequence)
print(bucket_sort(sequence))
常见排序算法复杂度总结
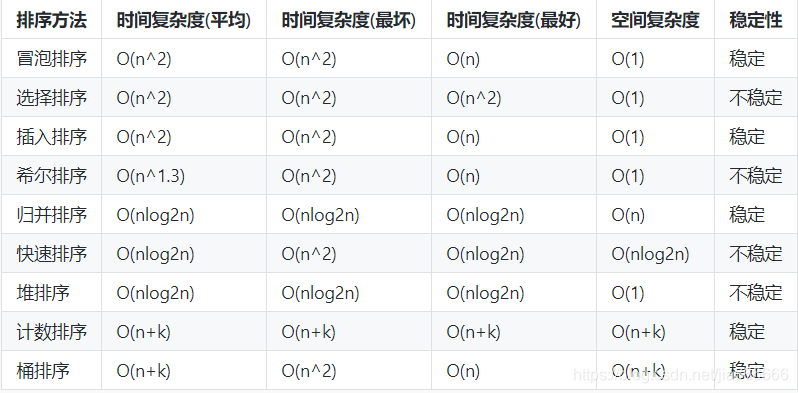
来源:CSDN
作者:jia666666
链接:https://blog.csdn.net/jia666666/article/details/103769568