什么是动态规划？

斐波那契数列 Fibonacci Sequence

F(0) = 1，F(1) = 1，F(n) =F(n-1) + F(n-2)

int fib (int n) {
    
	if (n == 0) {
        return 0;
	}
	if (n == 1) {
        return 1;
	}
    
	return fib(n-1) + fib(n-2);
}

fib(10) = 55 time : 4 e-06 s

fib(20) = 6765 time : 0.000104 s run function fib() 21891 times

fib(40) = 102334155 time : 1.28333 s run function fib() 331160281 times

fib(42) = 267914296 time : 3.47917 s

指数级别的复杂度，O(2^n)

递归树：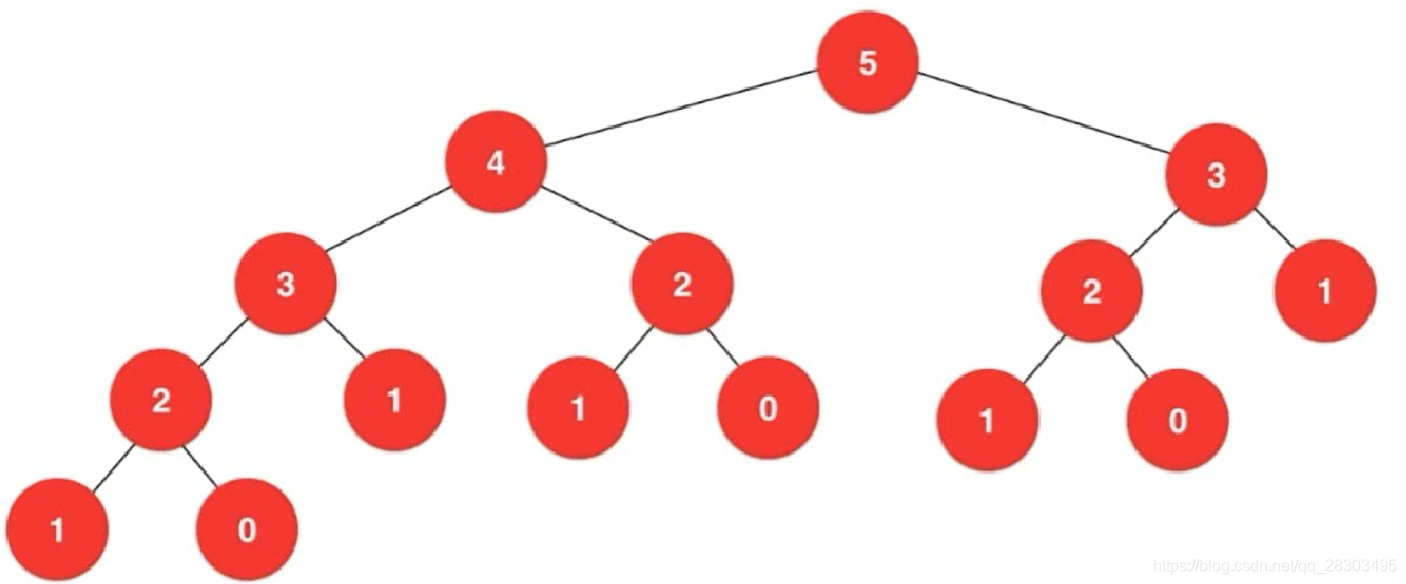
在这里插入图片描述

在递归树中进行了大量的重复计算，run function fib(20) 21891 times；run function fib(40) 331160281 times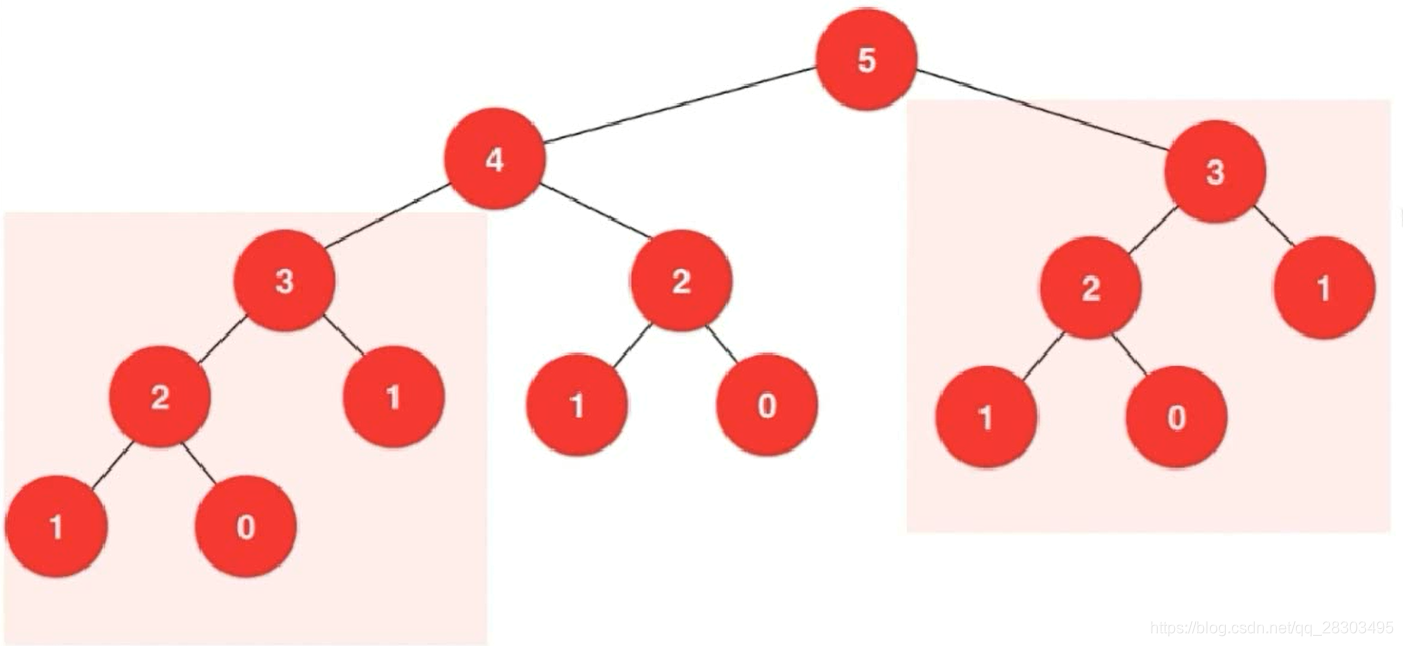
在这里插入图片描述

记忆化搜索

自上而下的解决问题，利用一个 memo 存放已经计算的结果

vector<int> memo;

int fib (int n) {
	if (n == 0) {
    	return 0;
	}
	if (n == 1) {
    	return 1;
	}
	
	if (memo[n] == -1) {
        memo[n] = fib(n-1) + fib(n-2);
	}
	
	return memo[n];
}

fib(40) = 102334155 time: 5e-06 s run function fib() 79 times.

fib(1000) = 1556111435 time : 6.5e-05 s run function fib() 1999 times.

（fib(1000) = 1556111435 这个值是错误的，超出了int整数的溢出值）

函数被调用的次数的 2^(n-1)

算法复杂度，O(n) 级别

动态规划

自下而上的解决问题

int fib (int n) {

	vector<int> memo(n+1, -1);
	
	nemo[0] = 0;
	memo[1] = 1; 
	for (int i = 2; i <= n; i++) {
        memo[i] = memo[i-1] + memo[i-2];
	}
	return memo[n];
}

时间复杂度，O(n)

fib(1000) = 1556111435（错误） time : 6e-05 s

dynamic programming（also known as dynamic optimization）is a method for solving a complex problem by breaking it down into a collection of simple subproblems，solving each of those subproblems just once，and storing their solutions -ideally，using a memory-based data structure.

将原问题拆解成若干子问题，同时保存子问题的答案，使得每个子问题只求解一次，最终获得原问题的答案。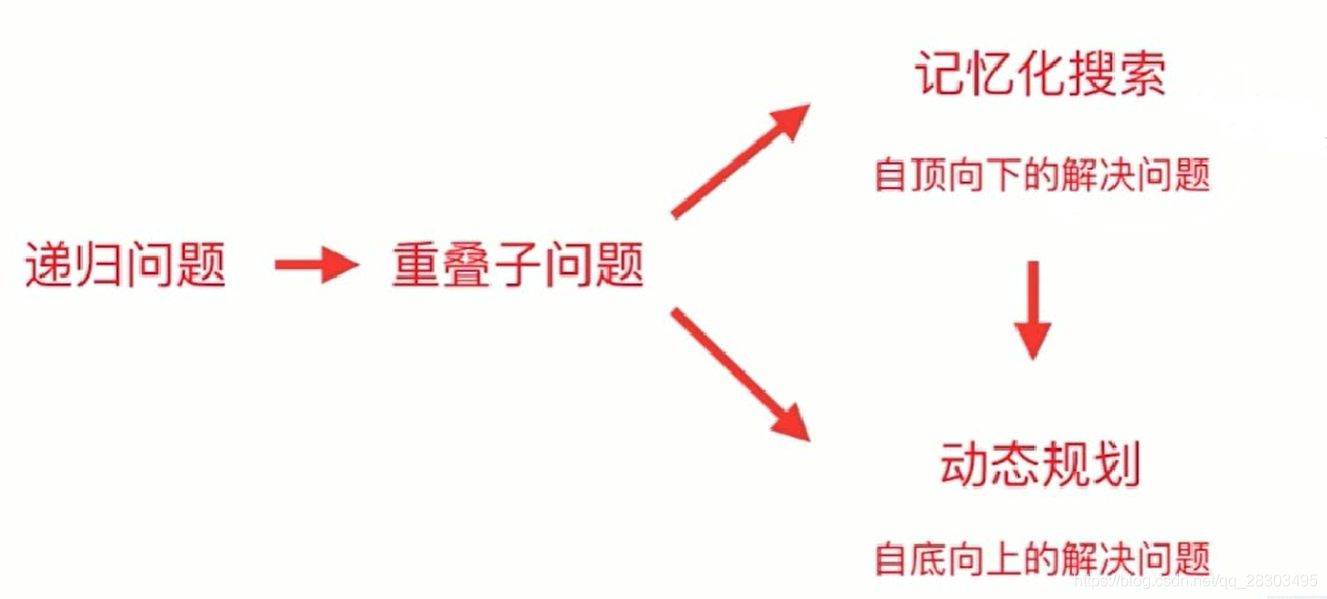
在这里插入图片描述

来源：CSDN

作者：慢行慢行

链接：https://blog.csdn.net/qq_28303495/article/details/103777925

标签

动态规划