1.学习总结
1.1树结构思维导图
ps:因为树的内容有点儿多所以字太小了,单击右键点全屏观看图片效果更佳哦~
1.2 树结构学习体会
在本章树的学习中,可以说是掌握得特别虚。因为二叉树的很多操作中都应用到了递归,而在上学期学习递归的时候就没有掌握好,很多时候树的几个递归代码会让我沉思很久才能屡清楚整个过程,然而看懂代码和会写代码还是有很大差别的,本次的PTA在课本上可以找到很多相关的代码情况下还是完成得跌跌撞撞的,更不敢想象如果是没有遇到过的需要用递归思想完成的题目我会做得多糟糕。除此之外的二叉树的线索化和遍历的过程我还是非常懵逼的,对二叉树的非递归遍历我也掌握得不清楚。因为错过了并查集的讲解内容,所以对并查集的整个过程目前也是很虚。关于二叉树的应用,比如说赫夫曼树和赫夫曼编码目前只是掌握了手动求解,但是转换成代码来实现的话怕是也会遇到很多的困难。
2.PTA实验作业
2.1 题目1: jmu-ds-表达式树
2.2 设计思路
void InitExpTree(BTree &T,string str)
{
建Op栈,Op.push('#')
初始化根节点栈,Stacktree栈
while(表达式未结束)
{
if(ch==操作数)
生成一个只有根节点的子树T
Stacktree.push(T)
if(ch==运算符)
{
while(ch<op栈顶运算符) 栈顶优先级高,则
{
创建一个树结点T,数据为Op.top()
Stacktree栈出2个根节点T1,T2
T->lchild=T1
T->rchild=T2
stacktree.push (T);
if(ch==op栈顶运算符) 则Op.pop();break;
}
if(ch不为')') 则Op.push(ch);
}
}
while(Op栈不为空)
{
创建一个树结点T,数据为Op.top()
Stacktree栈出2个根节点T1,T2
T->lchild=T1
T->rchild=T2
stacktree.push (T);
}
T = Stacktree.top()
}
double EvaluateExTree( BTree T )
{
if(T->data为数字) 则返回T->data
switch(T->data)
若为'+': return EvaluateExTree( T->lchild ) + EvaluateExTree( T->rchild );
若为'-':return EvaluateExTree( T->lchild ) - EvaluateExTree( T->rchild );
若为'*': return EvaluateExTree( T->lchild ) * EvaluateExTree( T->rchild );
若为'/': return EvaluateExTree( T->lchild ) / EvaluateExTree( T->rchild );
}
2.3 代码截图


2.4 PTA提交列表说明。

- A1:运行崩溃


- Q1:问题出在忽略了与或的优先级,与的优先级大于或,故前两个与结果跟后一条一句又形成或的关系运算,也就是说后一条语句是单独个体,而没有判断Op栈是否有元素就进行了Op.top()运算,故是一种危险状态,导致了运行崩溃
- A2:求解表达式的递归过程没有头绪
- Q2:询问同学的思路后才知道怎么写...只能说递归可不那么容易想清楚的...
- A3:除数为0的时候不知道要怎么结束这个程序
- Q3:利用exit(0)就可以巧妙解决这个问题啦~

2.1 题目2: jmu-ds-二叉树层次遍历
2.2 设计思路
BTree trans(string str,int i) //顺序存储结构转为二叉链存储结构
{
if(i大于等于结点数组长度或者i小于0)return NULL;
if(str[i]=='#')return NULL;
创建根结点b;
b->data = str[i];
b->k = 该结点所在的层数;
创建左子树:
b->left = trans(str,2*i);
创建右子树:
b->right = trans(str,2*i+1);
返回b结点;
}
void LevelOrder(BTree bt) //层次遍历二叉树
{
queue<BTree>q;
BTree p;
if(根结点不为空) 根结点入队列
while(队列不为空)
{
q出队列一个元素并把值赋给p;
输出p->data;
if(p的左孩子不为空)p的左孩子入队列;
if(p的右孩子不为空)p的右孩子入队列;
}
}
2.3 代码截图


2.4 PTA提交列表说明。

Q1:二叉树为空的时候输出结果错误


A1:考虑到只有一个#的空树情况:在trans函数中把递归结束条件i>str.size()改成i>=str.size() return;
2.1 题目3:7-8 jmu-ds-二叉树叶子结点带权路径长度和
2.2 设计思路
int WPL = 0;
BinTree trans(string str,int i) //把二叉树的顺序存储结构转成二叉链
{
if(i大于等于结点数组长度或者i小于0)return NULL;
if(str[i]=='#')return NULL;
创建根结点b;
b->data = str[i];
b->k = 该结点所在的层数;
创建左子树:
b->left = trans(str,2*i);
创建右子树:
b->right = trans(str,2*i+1);
返回b结点;
}
void get_wpl(BinTree b) //二叉树所有叶子结点的带权路径长度和
{
if(b为空结点) return;
if(b为叶子结点) WPL = WPL+(b的结点数据)*(b所在的层数-1);
调用函数求出b的左子树WPL;
调用函数求出b的右子树WPL;
}
2.3 代码截图


2.4 PTA提交列表说明。


- Q1:一开始抖机灵想直接通过顺序存储的数组利用二叉树的层数与下标之间的关系直接找到最后一层结点然后进行WPL的计算
- A1:但是这种做法只适合于叶子结点只在最后一层出现的情况,比如样例,故只通过了一个测试点。叶子结点可不只会出现在最后一个结点的呀喂!
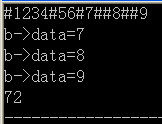
- Q2:样例是对的
 ,但是其他测试数据都是错误
,但是其他测试数据都是错误

- A2:边界问题:把trans函数中的i>str.size()改成i>=str.size()就正确了。
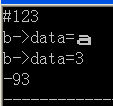
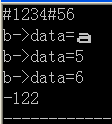
- 反思:边界的时候特别容易出错,#123出错,调试的时候输入变量b->Left->data,发现没错,是2,再输入b->Right->data,发现没错是3,又输入b->Left->Left发现不是0,即不是null,再输入b->Left->Left->data,发现是'\0',所以知道建树的时候把末尾也算进去了。
3.截图本周题目集的PTA最后排名
3.1 PTA排名

3.2 我的得分:
2.5
4. 阅读代码
#include <iostream>
#include <cstdlib>
#include <cmath>
#include <queue>
using namespace std;
struct tree
{
int data;
tree *l,*r;
tree()
{
l = r = NULL;
}
}*root;
void level()
{
int flag = 1,c = 0,e = 0;
queue<tree *>q;
if(root)q.push(root);
while(!q.empty())
{
int d = 0;
if(q.front() -> l)q.push(q.front() -> l),d ++;
if(q.front() -> r)
{
q.push(q.front() -> r);
if(!d)flag = 0;
else d ++;
}
if(c && d > e)flag = 0;
e = d;
if(c)cout<<' '<<q.front() -> data;
else
{
c = 1;
cout<<q.front() -> data;
}
q.pop();
}
cout<<endl;
if(flag)cout<<"YES";
else cout<<"NO";
}
tree *insert_(tree *node,int d)
{
if(node == NULL)
{
node = new tree();
node -> data = d;
}
else if(d > node -> data)node -> l = insert_(node -> l,d);
else node -> r = insert_(node -> r,d);
return node;
}
int main()
{
int n,d;
cin>>n;
root = NULL;
for(int i = 0;i < n;i ++)
{
cin>>d;
root = insert_(root,d);
}
level();
return 0;
}
- 代码功能:将一系列给定数字顺序插入一个初始为空的二叉搜索树(定义为左子树键值大,右子树键值小),判断最后的树是否一棵完全二叉树,并且给出其层序遍历的结果。
- 代码优点:巧妙利用完全二叉树的定义叶子结点只能出现在最后一层和以及最后一层的上一层且最后一层的结点靠左,不能存在只有右结点的结点,层序遍历中,每个结点的孩子数不能大于上一个结点的孩子数。
5. 代码Git提交记录截图


来源:https://www.cnblogs.com/lyq622/p/8994800.html
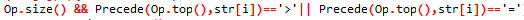

 ,但是其他测试数据都是错误
,但是其他测试数据都是错误