本篇随笔是数据科学家学习第八周的内容,主要参考资料为:
K-Means:
https://www.jianshu.com/p/caef1926adf7
深入理解K-Means聚类算法:
https://blog.csdn.net/taoyanqi8932/article/details/53727841
极客时间数据分析 - 聚类学习
用scikit-learn学习K-Means聚类
https://www.cnblogs.com/pinard/p/6169370.html
- 聚类
聚类试图将数据集中的样本划分为若干个通常是不相交的子集,每个子集成为一个“簇”。通过这样的划分,每个簇可能对应于一些潜在的概念(也就是类别),如“浅色瓜” “深色瓜”,“有籽瓜” “无籽瓜”,甚至“本地瓜” “外地瓜”等;需说明的是,这些概念对聚类算法而言事先是未知的,聚类过程仅能自动形成簇结构,簇对应的概念语义由使用者来把握和命名。
簇内的样本相关性越大,簇间相关性越小,则聚类效果越好。
- K-Means的原理和公式
对于给定的样本集,按照样本之间的距离大小,将样本集划分为K个簇。让簇内的点尽量紧密的连在一起,而让簇间的距离尽量的大。
对于距离大小的计算,有:

给定样本集D,K-Means算法针对聚类所得簇划分C最小化平方误差。
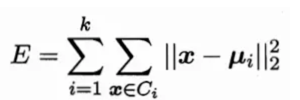
最小化上面的公式并不容易,找到它的最优解需考察样本集D内所有可能的簇划分,这是一个NP-hard问题。因此,K-Means算法采用了贪心算法,通过迭代优化来近似求解上面的公式。

- K-Means算法的缺陷
- K值需要预先给定,而K值如何预先设定比较困难
- K-Means算法对初始选取的聚类中心点(即初始均值向量)是敏感的,不同的随机种子点得到的聚类结果完全不同
- 对噪点过于敏感,因为算法是根据基于均值的
- 结果不一定是全局最优,只能保证局部最优(个人理解是因为基于贪心算法,而贪心算法就是保证局部最优解。)
- K-Means算法的改进
- 算法上的改进:bisecting K-means
- 计算性能上的改进:Mini Batch k-Means
- K值的评估
簇内的稠密程度和簇间的离散程度来评估聚类的效果。常见的方法有轮廓系数Silhouette Coefficient和Calinski-Harabasz Index。参见
来源:https://www.cnblogs.com/favor-dfn/p/12111219.html