激活函数 | 易学教程

为什么要引入激活函数？

为神经网络引入非线性属性，也就是说，我们希望神经网络既能计算线形函数，也能计算非线性函数。

1.sigmoid

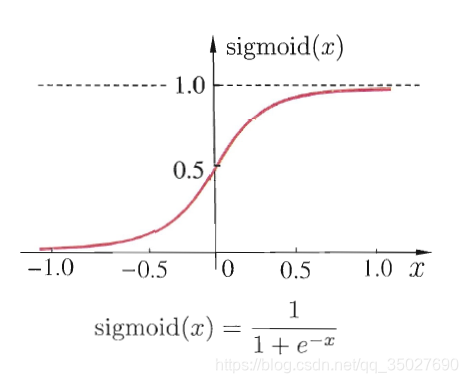
在这里插入图片描述
优点：

输出在0-1之间，单调连续，输出范围有限
容易求导： $f{\left( x \right)^\prime } = f\left( x \right)\left( {1 - f\left( x \right)} \right)$
缺点：
导致模型的梯度消失
误差反向传播时会有： $\frac{{\partial E}}{{\partial y\left( x \right)}}\frac{{\partial y\left( x \right)}}{{\partial \theta }}$ ，而一次反向传播，对激活函数有： $\frac{{\partial \sigma \left( x \right)}}{{\partial \theta }} = \sigma (1 - \sigma ) < 1$ ,这样反向传播多次以后，会有 ${\left( {\sigma (1 - \sigma )} \right)^n} \to {\rm{0}}$ ,也就是梯度会消失，参数没有办法学习。
输出不是以0为基准的，(函数值总为正的，权重的梯度会全部为正或者为负，这会导致梯度向完全不同的方向更新，使得优化困难)
指数运算比较慢，计算机使用泰勒展开求的。

2.tanh

因为sigmoid函数不是以0为基准，想把它变为0为基准，一个简单的办法是把sigmoid乘2-1，把0.5那一点拉回原点。这就得到了tanh函数

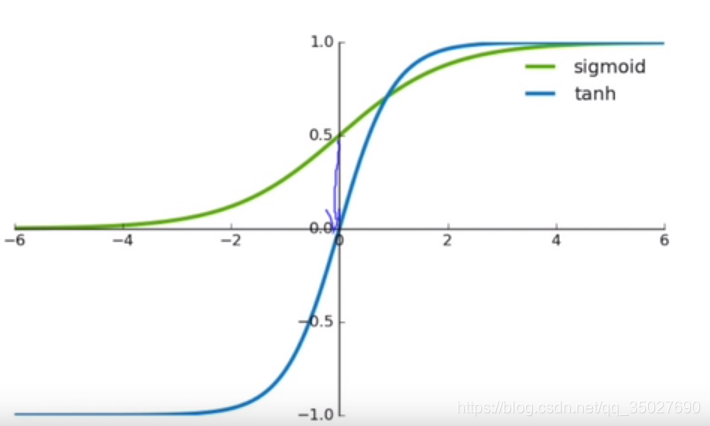
在这里插入图片描述

$f(x) = \tanh (x) = \frac{{{e^x} - {e^{ - x}}}}{{{e^x} + {e^{ - x}}}}$
${\rm{ = }}\frac{{1 - {e^{ - 2x}}}}{{1 + {e^{ - 2x}}}}$
${\rm{ = }}\frac{2}{{1 + {e^{ - 2x}}}} - 1$
${\rm{ = 2sigmoid(2x) - 1}}$
优点：

收敛速度比sigmoid快
因为均值在原点，输出中心以0为中心
缺点：
梯度消失
指数运算

为什么要以0为中心？对sigmoid而言取其梯度，中心点在0.5，则均值在0.5处，当大量的数据叠加的时候，再进行反向传播时，会导致其均值不断叠加，见下图红点处。但如果刚开始均值就在零点处，后面也一直会在零点附近波动，使得梯度可以控制。

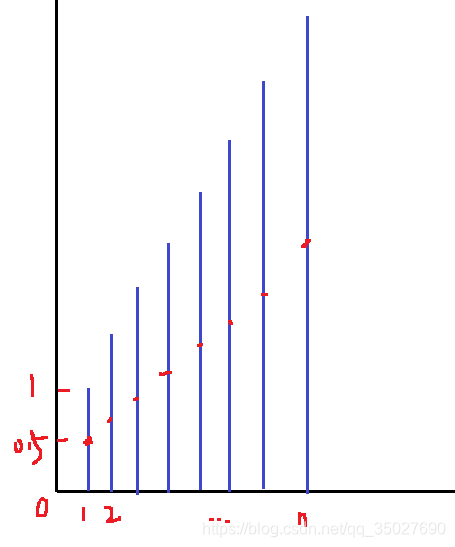
在这里插入图片描述

3.1 Relu

$f\left( x \right) = \max (x,0)$
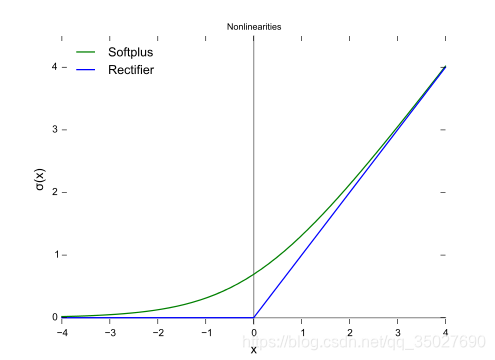
在这里插入图片描述
优点：

非饱和，收敛速度快
计算简单
缓解了梯度消失问题，导数是个常数
缺点：
在x小于0的时候，梯度为0，参数无法更新，会导致神经元出现死亡

3.2 Leaky Relu / PRelu

为了防止神经元死亡的问题，在x负半轴,把那部分的梯度变为一个很小的值，比如说图中乘以一个很小的系数：

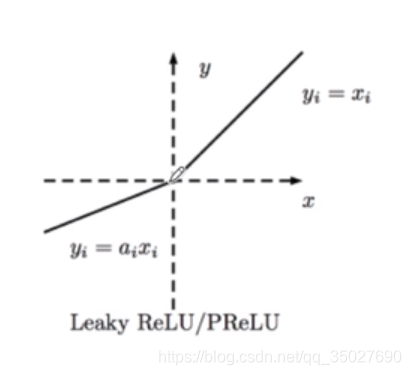
在这里插入图片描述
Leaky Relu中该系数是固定的，是人为定义的。
PRelu中该系数是通过数据学习到的，而不是预先定义的。

3.3 Leaky Relu / PRelu

还有一种是RRelu,即该系数的范围是从一个均匀的分布中随机抽取的数值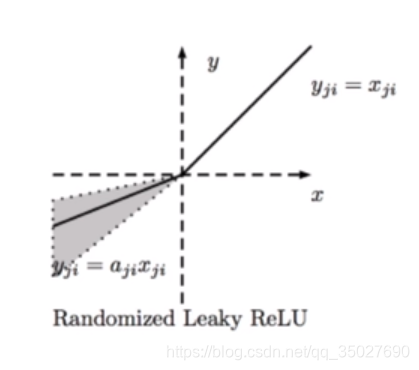
在这里插入图片描述

关于relu的总结：
常用于隐藏层，很少用于输出的激活函数
输出层如果是多分类问题，用softmax函数，如果是回归问题，用线形函数
参考：https://www.bilibili.com/video/av43533515?from=search&seid=12719173884000066379

来源：CSDN

作者：小研一枚

链接：https://blog.csdn.net/qq_35027690/article/details/103730952

标签

sigmoid

relu

梯度