究竟什么是时间复杂度呢?让我们来想象一个场景:某一天,小灰和大黄同时加入了一个公司......
一天过后,小灰和大黄各自交付了代码,两端代码实现的功能都差不多。大黄的代码运行一次要花100毫秒,内存占用5MB。小灰的代码运行一次要花100秒,内存占用500MB。于是......
由此可见,衡量代码的好坏,包括两个非常重要的指标:
1.运行时间;
2.占用空间。
关于代码的基本操作执行次数,我们用四个生活中的场景,来做一下比喻:
场景1:
给小灰一条长10寸的面包,小灰每3天吃掉1寸,那么吃掉整个面包需要几天?
答案自然是 3 X 10 = 30天。
如果面包的长度是 N 寸呢?
此时吃掉整个面包,需要 3 X n = 3n 天。
如果用一个函数来表达这个相对时间,可以记作 T(n) = 3n。
场景2:
给小灰一条长16寸的面包,小灰每5天吃掉面包剩余长度的一半,第一次吃掉8寸,第二次吃掉4寸,第三次吃掉2寸......那么小灰把面包吃得只剩下1寸,需要多少天呢?
这个问题翻译一下,就是数字16不断地除以2,除几次以后的结果等于1?这里要涉及到数学当中的对数,以2位底,16的对数,可以简写为log(2)16。
因此,把面包吃得只剩下1寸,需要 5 X log(2)16 = 5 X 4 = 20 天。
如果面包的长度是 N 寸呢?
需要 5 X logn = 5log(2)n天,记作 T(n) = 5log(2)n。
场景3:
给小灰一条长10寸的面包和一个鸡腿,小灰每2天吃掉一个鸡腿。那么小灰吃掉整个鸡腿需要多少天呢?
答案自然是2天。因为只说是吃掉鸡腿,和10寸的面包没有关系 。
如果面包的长度是 N 寸呢?
无论面包有多长,吃掉鸡腿的时间仍然是2天,记作 T(n) = 2。
场景4:
给小灰一条长10寸的面包,小灰吃掉第一个一寸需要1天时间,吃掉第二个一寸需要2天时间,吃掉第三个一寸需要3天时间.....每多吃一寸,所花的时间也多一天。那么小灰吃掉整个面包需要多少天呢?
答案是从1累加到10的总和,也就是55天。
如果面包的长度是 N 寸呢?
此时吃掉整个面包,需要 1+2+3+......+ n-1 + n = (1+n)*n/2 = 0.5n^2 + 0.5n。
记作 T(n) = 0.5n^2 + 0.5n。
上面所讲的是吃东西所花费的相对时间,这一思想同样适用于对程序基本操作执行次数的统计。刚才的四个场景,分别对应了程序中最常见的四种执行方式:
场景1:T(n) = 3n,执行次数是线性的。
void eat1(int n)
{ for(int i=1; i<=n; i++)
s+=3;
}
场景2:T(n) = 5log(2)n,执行次数是对数的。
void eat2(int n)
{ for(int i=1; i<n; i*=2)
s++;
}
场景3:T(n) = 2,执行次数是常量的。
void eat3(int n)
{ s=n;
}
场景4:T(n) = 0.5n^2 + 0.5n,执行次数是一个多项式。
void eat4(int n)
{ s=0;
for(int i=1; i<=n; i++)
for(int j=1; j<=i; j++)
s++;
}
渐进时间复杂度
有了基本操作执行次数的函数 T(n),是否就可以分析和比较一段代码的运行时间了呢?还是有一定的困难。
比如算法A的相对时间是T(n)= 100n,算法B的相对时间是T(n)= 5n^2,这两个到底谁的运行时间更长一些?这就要看n的取值了。所以,这时候有了渐进时间复杂度的概念,官方的定义如下:
若存在函数 f(n),使得当n趋近于无穷大时,T(n)/ f(n)的极限值为不等于零的常数,则称 f(n)是T(n)的同数量级函数。记作 T(n)= O(f(n)),称O(f(n)) 为算法的渐进时间复杂度,简称时间复杂度。
渐进时间复杂度用大写O来表示,所以也被称为大O表示法。
让我们回头看看刚才的四个场景。
场景1:
T(n) = 3n
最高阶项为3n,省去系数3,转化的时间复杂度为:
T(n) = O(n)
场景2:
T(n) = 5logn
最高阶项为5logn,省去系数5,转化的时间复杂度为:
T(n) = O(logn)
场景3:
T(n) = 2
只有常数量级,转化的时间复杂度为:
T(n) = O(1)
场景4:
T(n) = 0.5n^2 + 0.5n
最高阶项为0.5n^2,省去系数0.5,转化的时间复杂度为:
T(n) = O(n^2)
这四种时间复杂度究竟谁用时更长,谁节省时间呢?稍微思考一下就可以得出结论:
O(1)< O(logn)< O(n)< O(n^2)
时间复杂度的巨大差异
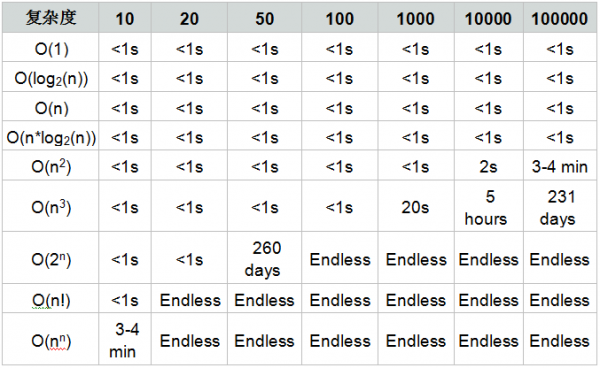
我们来举过一个栗子:
算法A的相对时间规模是T(n)= 100n,时间复杂度是O(n)
算法B的相对时间规模是T(n)= 5n^2,时间复杂度是O(n^2)
算法A运行在小灰家里的老旧电脑上,算法B运行在某台超级计算机上,运行速度是老旧电脑的100倍。
那么,随着输入规模 n 的增长,两种算法谁运行更快呢?
从表格中可以看出,当n的值很小的时候,算法A的运行用时要远大于算法B;当n的值达到1000左右,算法A和算法B的运行时间已经接近;当n的值越来越大,达到十万、百万时,算法A的优势开始显现,算法B则越来越慢,差距越来越明显。
这就是不同时间复杂度带来的差距。
一、概念
时间复杂度是总运算次数表达式中受n的变化影响最大的那一项(不含系数)
(1)时间频度
一个算法执行所耗费的时间,从理论上是不能算出来的,必须上机运行测试才能知道。但我们不可能也没有必要对每个算法都上机测试,只需知道算法花费的时间多少
一个算法花费的时间与算法中语句的执行次数成正比例,哪个算法中语句执行次数多,它花费时间就多。
一个算法中的语句执行次数称为语句频度或时间频度。记为T(n)。
(2)时间复杂度
n称为问题的规模,当n不断变化时,时间频度T(n)也会不断变化。但有时我们想知道它变化时呈现什么规律。为此,我们引入时间复杂度概念。
一般情况下,算法中基本操作重复执行的次数是问题规模n的某个函数,用T(n)表示,若有某个辅助函数f(n),使得当n趋近于无穷大时,T(n)/f(n)的极限值为不等于零的常数,则称f(n)是T(n)的同数量级函数。记作T(n)=O(f(n)) 称O(f(n)) 为算法的渐进时间复杂度,简称时间复杂度。
注意,时间频度与时间复杂度是不同的,时间频度不同但时间复杂度可能相同。
如:T(n)=n^2+3n+4与T(n)=4n2+2n+1它们的频度不同,但时间复杂度相同,都为O(n^2)。
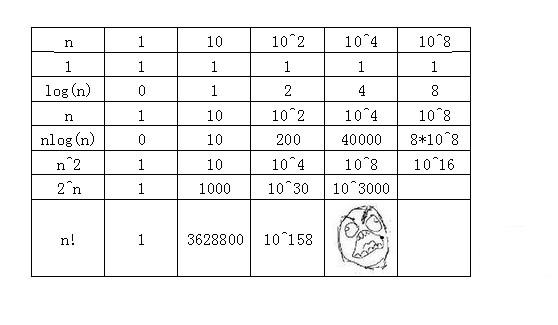
常见的时间复杂度有:
常数阶O(1) < 对数阶O(log2n) < 线性阶O(n) < 线性对数阶O(nlog2n) < 平方阶O(n^2) <
立方阶O(n^3) < k次方阶O(n^k) < 指数阶O(2^n) < 阶乘阶O(n!) < O(n^n)
(3)最坏时间复杂度和平均时间复杂度 最坏情况下的时间复杂度称最坏时间复杂度。一般不特别说明,讨论的时间复杂度均是最坏情况下的时间复杂度。 这样做的原因是:最坏情况下的时间复杂度是算法在任何输入实例上运行时间的上界,这就保证了算法的运行时间不会比任何更长。
在最坏情况下的时间复杂度为T(n)=0(n),它表示对于任何输入实例,该算法的运行时间不可能大于0(n)。 平均时间复杂度是指所有可能的输入实例均以等概率出现的情况下,算法的期望运行时间。
指数阶0(2n),显然,时间复杂度为指数阶0(2n)的算法效率极低,当n值稍大时就无法应用。
二、最坏时间复杂度和平均时间复杂度
对于时间复杂度的分析,一般是这两种方法:
(1)最坏时间复杂度
最坏情况运行时间(运行时间将不会再坏了。通常,除非特别指定,我们提到的运行时间都是最坏情况的运行时间
对于追问为什么是最坏时间复杂度的好奇宝宝:
1、如果最差情况下的复杂度符合我们的要求,我们就可以保证所有的情况下都不会有问题。
2、也许你觉得平均情况下的复杂度更吸引你(见下),但是:第一,难计算第二,有很多算法的平均情况和最差情况的复杂度是一样的. 第三,而且输入数据的分布函数很可能是你没法知道。
(2)平均时间复杂度
平均时间复杂度也是从概率的角度看,更能反映大多数情况下算法的表现。当然,实际中不可能将所有可能的输入都运行一遍,因此平均情况通常指的是一种数学期望值,而计算数学期望值则需要对输入的分布情况进行假设。平均运行时间很难通过分析得到,一般都是通过运行一定数量的实验数据后估算出来的。
三、如何推导出时间复杂度,有如下几个原则:
1、如果运行时间是常数量级,用常数1表示;
2、只保留时间函数中的最高阶项;
3、如果最高阶项存在,则省去最高阶项前面的系数。
一、单项选择题
1.个算法应该是( )。
A.程序 B.问题求解步骤的描述 C.要满足五个基本特性 D. A和C
2.某算法的时间复杂度为O(n^2),表明该算法的( )。
A.问题规模是n^2 B.执行时间等于n^2
C.执行时间与n^2成正比 D.问题规模与n^2成正比
3.以下算法的时间复杂度为( )。
void fun(int n)
{ int i=l;
while(i<=n)
i=i*2;
}
A. O(n) B. O(n2) C. O(nlog2n) D. O(log2n)
4.【2011年计算机联考真题】设n是描述问题规模的非负整数,下面程序片段的时间复杂度是()。
x=2;
while(x<n/2)
x=2*x;
A. O(log2n) B. O(n) C. O(nlog2n) D. O(n2)
5.【2012年计算机联考真题】求整数n (n>=0)阶乘的算法如下,其时间复杂度是( )。
int fact(int n)
{ if (n<=l) return 1;
return n*fact(n-1);
}
A. O(log2n) B. O(n) C. O(nlog2n) D. O(n2)
6.有以下算法,其时间复杂度为( )。
void fun (int n)
{ int i=0;
while(i*i*i<=n) i++;
}
A. O(n) B. O(nlogn) C. D.
7.程序段如下,其中n为正整数,则最后一行的语句频度在最坏情况下是( )。
for(i=n-l;i>l;i--)
for(j=1;j<i;j++)
if (A[j]>A[j+l]) A[j]与 A[j+1]对换;
A. O(n) B. O(nlogn) C. O(n3) D. O(n2)
8.以下算法中加下划线语句的执行次数为()。
int m=0, i, j;
for(i=l;i<=n;i++)
for(j=1;j<=2*i;j++) m++;
A. n(n+1) B. n C. n+1 D. n2
9.下面说法错误的是( )。
Ⅰ.算法原地工作的含义是指不需要任何额外的辅助空间
Ⅱ.在相同的规模n下,复杂度O(n)的算法在时间上总是优于复杂度O(2n)的算法
Ⅲ.所谓时间复杂度是指最坏情况下,估算算法执行时间的一个上界
Ⅳ.同一个算法,实现语言的级别越高,执行效率就越低
A. Ⅰ B. Ⅰ、Ⅱ C. Ⅰ、Ⅳ D. Ⅲ
二、综合应用题
1.一个算法所需时间由下述递归方程表示,试求出该算法的时间复杂度的级别(或阶)。
式中,n是问题的规模,为简单起见,设n是2的整数幂。
2.分析以下各程序段,求出算法的时间复杂度。
程序段①
i=l;k=0;
while(i<n-l)
{ k=k+10*i;
i++;
}
- 程序段②
- y=0;
- while((y+1)*(y+1)<=n)
- y=y+1;
- // 程序段③
- for(i=l;i<=n;i++)
- for(j =1;j <=i;j ++)
- for(k=l;k<=j;k++)
- x++;
- // 程序段④
- for(i=0;i<n;i++)
- for(j=0;j<m;j++)
- a[i] [j]=0;
答案与解析
一、单项选择题
1. B
程序不一定满足有穷性,如死循环、操作系统等,而算法必须有穷。算法代表了对问题求解步骤的描述,而程序则是算法在计算机上的特定的实现。
2. C
时间复杂度为O(n2),说明算法的执行时间T(n)<=c * n2(c为比例常数),即T(n)=O(n2),时间复杂度T(n)是问题规模n的函数,其问题规模仍然是n而不是n2。
3. D
基本运算是i=i*2,设其执行时间为T(n),则2T(n)<=n,即T(n)<=log2n=O(log2n)。
4. A
在程序中,执行频率最高的语句为“x=2*x”。设该语句共执行了 t次,则2t+1=n/2,故t=log2(n/2)-1=log2n-2,得 T(n)=O(log2n)。
5. B
本题是求阶乘n!的递归代码,即n*(n-1)*...*1共执行n次乘法操作,故T(n)=O(n)。
6. C
算法的基本运算是i++,设其执行时间为T(n),则有,T(6)*T(n)*T(n)<=n,即T(n)3<=n。故有,。
更加直观和快速的解题方法:要计算语句i++的执行次数(由于每执行一次i加1),其中判断条件可理解为i3=n,即,因此有
。
7. D
当所有相邻元素都为逆序时,则最后一行的语句每次都会执行。此时,
所以在最坏情况下的该语句频度是O(n2)。
8. A
m++语句的执行次数为
9. A
Ⅰ,算法原地工作是指算法所需的辅助空间是常量。Ⅱ,题中是指算法的时间复杂度,不要想当然认为是程序(该算法的实现)的具体执行时间,而赋予n—个特殊的值。时间复杂度为O(n)的算法,必然总是优于时间复杂度为O(2n)的算法。Ⅲ,时间复杂度总是考虑在最坏情况下的时间复杂度,以保证算法的运行时间不会比它更长。Ⅳ为严蔚敏教材的原话。
二、综合应用题
1.解答:
时间复杂度为O(nlog2n)。
设n=2k(k>=0),根据题目所给定义,有,由此,可得一般递推公式
,进而,可得
,即
,即为
。
2.解答:
①基本语句是k=k+10*i,共执行了n-2次,所以T(n)=O(n)。
②设循环体共执行T(n)次,每循环一次,循环变量y加1,最终T(n)=y。故(T(n))2<=n,解得 T(n)=O(n1/2)。
③ x++是基本语句,。
④a[i][j]=0是基本语句,内循环执行m次,外循环执行n次,共执行了 m*n次,所以 T(m, n)=O(m*n)0
来源:CSDN
作者:流年15096301719
链接:https://blog.csdn.net/weixin_43736974/article/details/103651206