Python实现基本排序

排序是比较常用的算法，其实有很多种实现，比如冒泡排序，选择排序，归并排序，希尔排序，快速排序等，今天介绍使用python语言实现这几种排序算法。

冒泡排序

冒泡排序是最常见到的排序算法，也是大学学习时遇到的第一种排序算法，它的实现思想是：相邻的两个元素进行比较，然后把较大的元素放到后面（正向排序），在一轮比较完后最大的元素就放在了最后一个位置，因为这一点像鱼儿在水中吐的气泡在上升的过程中不断变大，所以得名冒泡排序。在该排序算法中，要遍历n-1轮，每一轮都要比较数组中的元素，所以时间复杂度是O(n2)。
在比较的过程中相同的元素并不会发生交换，所以冒泡排序是一种稳定的排序算法。

接下来看一个冒泡排序的图片

![在这里插入图片描述](https://img-blog.csdnimg.cn/2019122215314471.gif
具体代码实现

def bubble_sort(alist):
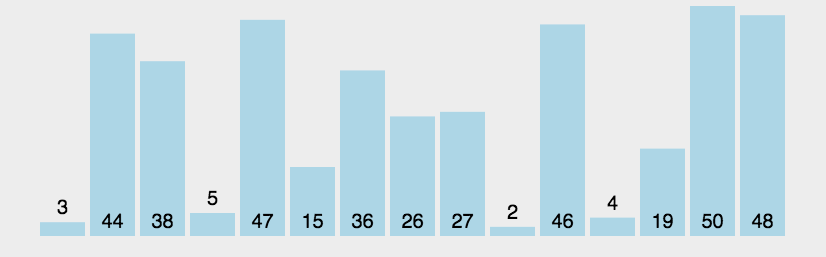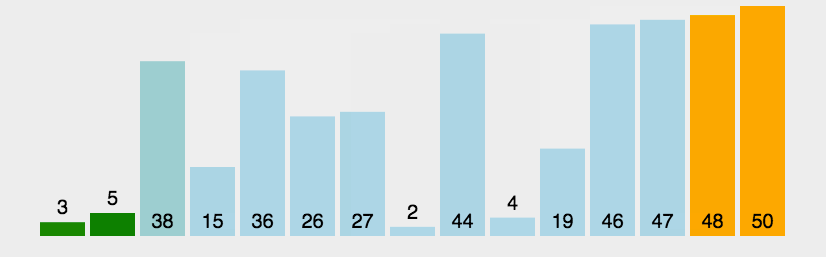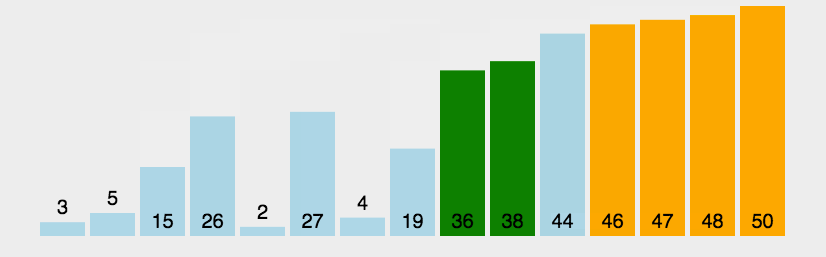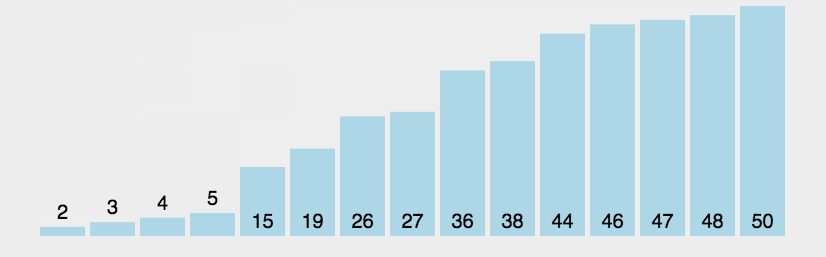
    length = len(alist)
    for i in range(length - 1):
        # i表示比较多少轮
        for j in range(length - i - 1):
            # j表示每轮比较的元素的范围，因为每比较一轮就会排序好一个元素的位置，
            # 所以在下一轮比较的时候就少比较了一个元素，所以要减去i
            if alist[j] > alist[j + 1]:
                alist[j], alist[j + 1] = alist[j + 1], alist[j]

选择排序

选择排序的思路是：第一轮的时候，所有的元素都和第一个元素进行比较，如果比第一个元素大，就和第一个元素进行交换，在这轮比较完后，就找到了最小的元素；第二轮的时候所有的元素都和第二个元素进行比较找出第二个位置的元素，以此类推。

每遍历一次排好一个元素，而每一次都会比较所有的元素，所以时间复杂度为O(n2)。因为在交换的过程中，相同的元素位置可能发生变化，所以选择排序是不稳定的。

接下来看一个选择排序的图片

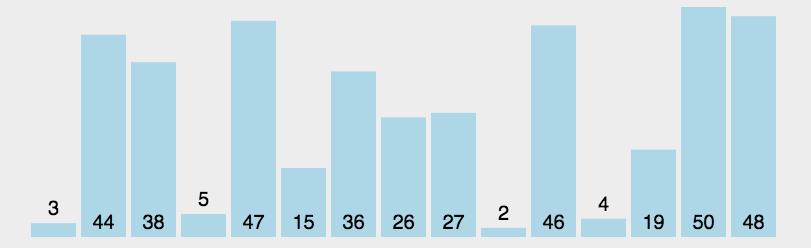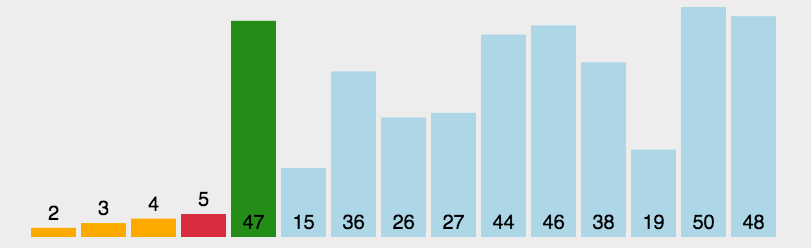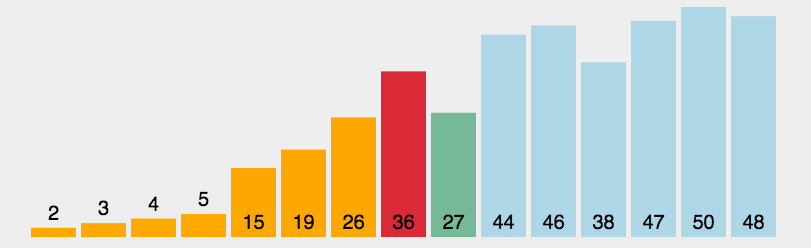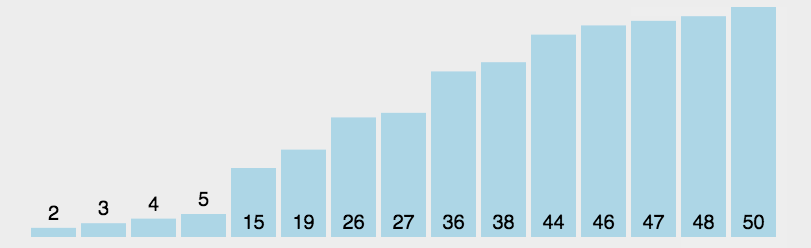
具体代码实现

def selection_sort(list_target):
    length = len(list_target)
    for r in range(length - 1, 0, -1):
        for c in range(r):
            if list_target[c] > list_target[r]:
                list_target[c], list_target[r] = list_target[r], list_target[c]


l = [8, 1, 12, 7, 6, 10, 3, 4, 8, 5, 9, 2, 11, 5, 13]
selection_sort(l)
print(l)

插入排序

插入排序的工作原理是通过构建有序序列，对于未排序数据，在已排序序列中从后向前扫描，找到相应位置并插入。插入排序在实现上，在从后向前扫描过程中，需要反复把已排序元素逐步向后挪位，为最新元素提供插入空间。
插入排序的时间复杂度为O(n2)。

看一下插入排序的图片

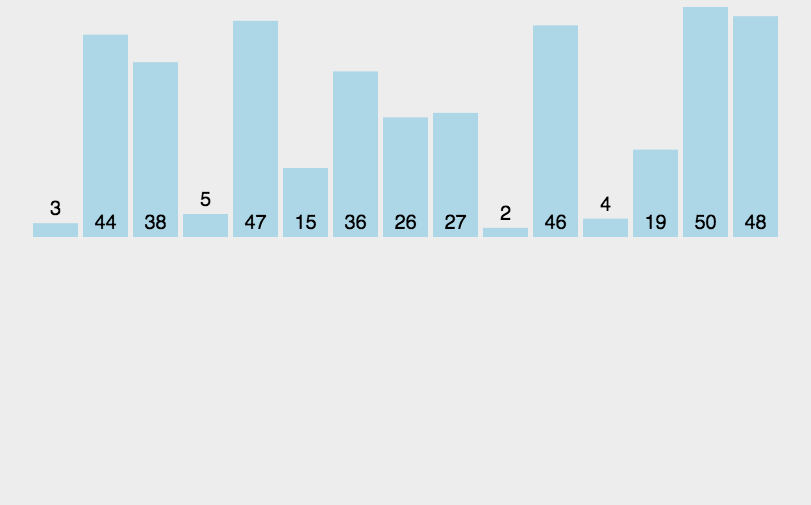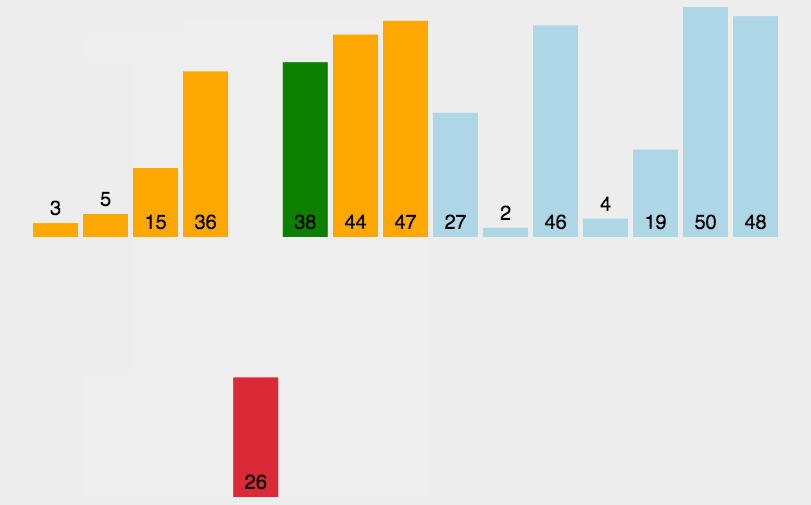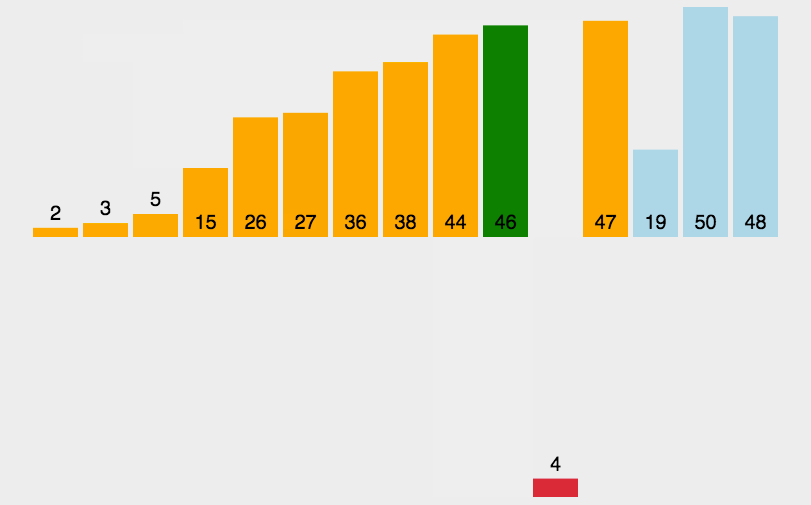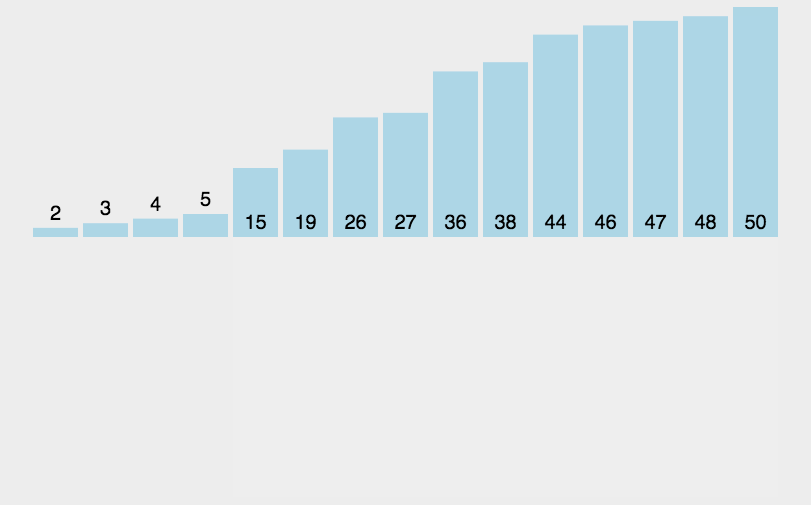
代码实现

def insert_sort(alist):
    for i in range(1, len(alist)):
        # 从第二个元素开始，每次取出一个元素，插入前面的序列使其有序
        for j in range(i, 0, -1):
            if alist[j] < alist[j - 1]:
                alist[j], alist[j - 1] = alist[j - 1], alist[j]

快速排序

快速排序（英语：Quicksort），又称划分交换排序（partition-exchange sort），通过一趟排序将要排序的数据分割成独立的两部分，其中一部分的所有数据都比另外一部分的所有数据都要小，然后再按此方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行，以此达到整个数据变成有序序列。

步骤为：

1.从数列中挑出一个元素，称为"基准"（pivot），一般是第一个元素。

2.重新排序数列，所有元素比基准值小的摆放在基准前面，所有元素比
	基准值大的摆在基准的后面（相同的数可以到任一边）。在这个分区结
	束之后，该基准就处于数列的中间位置。这个称为分区（partition）操作。
	
3.递归地（recursive）把小于基准值元素的子数列和大于基准值元素的子数列排序。

递归的最底部情形，是数列的大小是零或一，也就是永远都已经被排序好了。虽然一直递归下去，但是这个算法总会结束，因为在每次的迭代（iteration）中，它至少会把一个元素摆到它最后的位置去。

看一下快速排序的图片

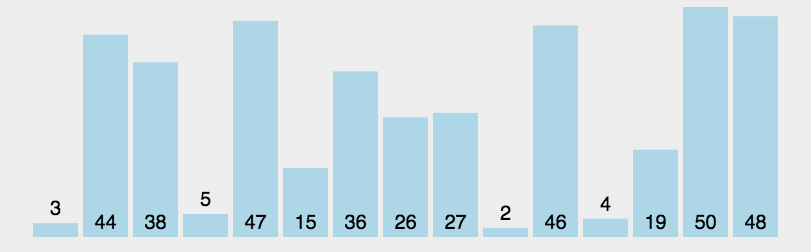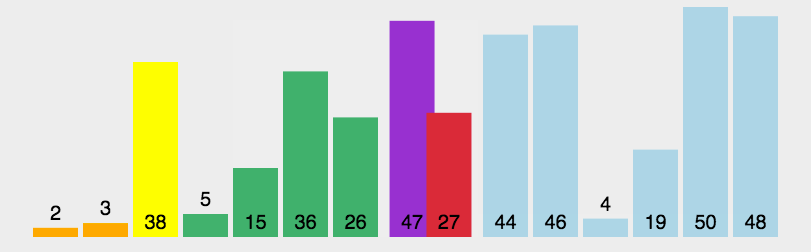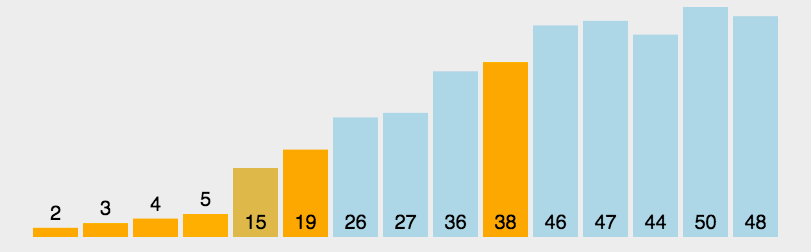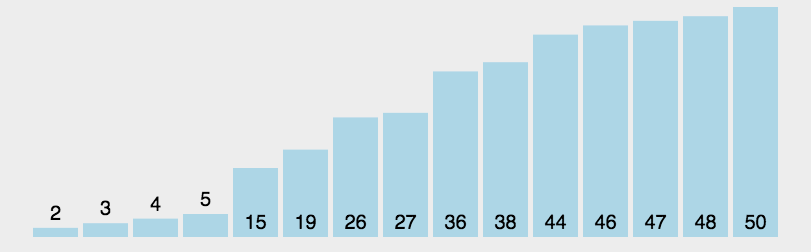
具体代码实现

"""
快速排序算法
"""


def sub_sort(l, low, high):
    x = l[low]  # 基准
    while low < high:
        # 如果后边的数比x大high向前走
        while l[high] > x and high > low:
            high -= 1
        l[low] = l[high]  # 比x小的往前甩
        # 如果前面的数比x小则low往后走
        while l[low] <= x and low < high:
            low += 1
        l[high] = l[low]  # 比x大的往后甩
    l[low] = x  # 将x插入最终位置
    return low  # 每一轮最终基准数确定的位置


# low : 第一个元素索引号,high: 最后一个元素索引号
"""
该写法表示希望low传一个整形,high传一个整形,返回值为None类型
但是没有强制要求必须这样做
"""


def quick(l: list, low: int, high: int) -> None:
    if low < high:
        key = sub_sort(l, low, high)
        quick(l, low, key - 1)
        quick(l, key + 1, high)


l = [8, 1, 12, 7, 6, 10, 3, 4, 8, 5, 9, 2, 11, 5, 13]
quick(l, 0, len(l) - 1)
print(l)

来源：CSDN

作者：BMW_princeMrwang

链接：https://blog.csdn.net/BMW_princeMrwang/article/details/103653775