| 20182311 2019-2020-1 《数据结构与面向对象程序设计》实验九报告 |
课程:《程序设计与数据结构》
班级: 1823
姓名: 冷冲
学号:20182311
实验教师:王志强
实验日期:2019年12月7日
必修/选修: 必修
1.实验内容
- 初始化:根据屏幕提示(例如:输入1为无向图,输入2为有向图)初始化无向图和有向图(可用邻接矩阵,也可用邻接表),图需要自己定义(顶点个数、边个数,建议先在草稿纸上画出图,然后再输入顶点和边数)
- 图的遍历:完成有向图和无向图的遍历(深度和广度优先遍历)
- 完成有向图的拓扑排序,并输出拓扑排序序列或者输出该图存在环
- 完成无向图的最小生成树(Prim算法或Kruscal算法均可),并输出
- 完成有向图的单源最短路径求解(迪杰斯特拉算法)
2. 实验过程及结果
(一)初始化:基于邻接矩阵构建有向图和无向图
import java.util.*;
public class Graph {
private int[][] matrix;//邻接矩阵
private char[] vexs;//顶点数组
private int vexnum;//节点数
private int arcnum;//边数
private int[] isVisited;//0表示未被访问。1表示访问过
private Queue list;
public Graph(int vexnum, int arcnum){
this.vexnum = vexnum;
this.arcnum = arcnum;
this.matrix = new int[20][20];
this.vexs = new char[20];
this.isVisited=new int[20];
this.list=new LinkedList();
}
//构建无向图的邻接矩阵
public void createUGraph(){
Scanner in=new Scanner(System.in);
//构建顶点数组
System.out.println("请输入顶点:");
for(int i=0;i<vexnum;i++)
vexs[i]=in.next().charAt(0);
//初始化邻接矩阵
for(int i=0;i<vexnum;i++)
for(int j=0;j<vexnum;j++)
matrix[i][j]=0;
//构建邻接矩阵
for(int p = 0; p < this.arcnum; p++) {
System.out.println("请输入每条边的头尾:");
char a = in.next().charAt(0);
char b = in.next().charAt(0);
int i = this.locateVex(a);
int j = this.locateVex(b);
this.matrix[i][j] = this.matrix[j][i] = 1; //对称阵
}
}
public int locateVex(char a){
for(int i=0;i<vexnum;i++){
if(vexs[i]==a)
return i;
}
return -1;
}
//构建有向图的邻接矩阵
public void createGraph(){
Scanner in=new Scanner(System.in);
System.out.println("请输入顶点:");
for(int i=0;i<vexnum;i++)
vexs[i]=in.next().charAt(0);
for(int i=0;i<vexnum;i++)
for(int j=0;j<vexnum;j++)
matrix[i][j]=0;
//构建邻接矩阵
for(int p = 0; p < this.arcnum; p++) {
System.out.println("请输入每条边的头尾:");
char a = in.next().charAt(0);
char b = in.next().charAt(0);
int i = this.locateVex(a);
int j = this.locateVex(b);
this.matrix[i][j]=1;
}
}
}
(二)遍历:BFS\DFS。使用邻接矩阵进行遍历,通过判别当前指向点的邻接点是否被遍历过,若无,则遍历,若当前点无可用的点,则原路返回,直到所有点都被遍历一遍。使用非递归方法可以直接写出简单的BFS实现,递归方法需要使用队列,代码如下:
public List getCurrent(int i){
List list1=new LinkedList();
for(int j=0;j<vexnum;j++){
if(matrix[i][j]==1&&isVisited[j]==0)
list1.add(vexs[j]);
}
return list1;
}
深度遍历方法:
//邻接矩阵的深度遍历,递归实现
public void DFSTraverse(int i){
DFS(this,i);
//遍历完成进行复位
for(int j=0;j<isVisited.length;j++)
isVisited[j]=0;
}
public void DFS(Graph a,int i){
isVisited[i]=1;
System.out.print(vexs[i]+"\t");
for(int j=0;j<vexnum;j++){
if(matrix[i][j]==1&&isVisited[j]==0){
DFS(a,j);
}
}
}
广度遍历方法:
//邻接矩阵的广度遍历,非递归实现
public void BFSTraverse(int i){
list.add(vexs[i]);
BFS();
for(int j=0;j<isVisited.length;j++)
isVisited[j]=0;
}
public void BFS(){
char temp=(char)list.poll();
int x=temp-'0';
isVisited[x]=1;
System.out.println(temp);
List nerborpointlist=getCurrent(x);
for(int i=0;i<nerborpointlist.size();i++){
char j=(char)nerborpointlist.get(i);
list.add(j);
int k=j-'0';
isVisited[k]=1;
}
if(!list.isEmpty()){
BFS();
}
}
(三)拓扑排序:基于邻接链表构成的图,编写图的节点和边类及构建图的方法,代码如下:
//点类
class VertexNode {
private int in;
private int data;
private EdgeNode firstEdge;
public VertexNode(int in, int data, EdgeNode firstEdge) {
super();
this.in = in;
this.data = data;
this.firstEdge = firstEdge;
}
public int getIn() {
return in;
}
public void setIn(int in) {
this.in = in;
}
public int getData() {
return data;
}
public void setData(int data) {
this.data = data;
}
public EdgeNode getFirstEdge() {
return firstEdge;
}
public void setFirstEdge(EdgeNode firstEdge) {
this.firstEdge = firstEdge;
}
}
//边类
class EdgeNode {
private int adjvex;
private int weight;
private EdgeNode next;
public EdgeNode(int adjvex, int weight, EdgeNode next) {
super();
this.adjvex = adjvex;
this.weight = weight;
this.next = next;
}
public int getAdjvex() {
return adjvex;
}
public void setAdjvex(int adjvex) {
this.adjvex = adjvex;
}
public int getWeight() {
return weight;
}
public void setWeight(int weight) {
this.weight = weight;
}
public EdgeNode getNext() {
return next;
}
public void setNext(EdgeNode next) {
this.next = next;
}
}
//构建图
public void createGraph3(){
VertexNode v0 = new VertexNode(1, 0, null);
EdgeNode v0e0 = new EdgeNode(4, 0, null);
v0.setFirstEdge(v0e0);
VertexNode v1 = new VertexNode(0, 1, null);
EdgeNode v1e0 = new EdgeNode(2, 0, null);
EdgeNode v1e1 = new EdgeNode(3, 0, null);
v1.setFirstEdge(v1e0);
v0e0.setNext(v1e1);
VertexNode v2 = new VertexNode(1, 2, null);
EdgeNode v2e0 = new EdgeNode(3, 0, null);
v2.setFirstEdge(v2e0);
VertexNode v3 = new VertexNode(2, 3, null);
EdgeNode v3e0 = new EdgeNode(0, 0, null);
EdgeNode v3e1 = new EdgeNode(4, 0, null);
v3.setFirstEdge(v3e0);
v3e0.setNext(v3e1);
VertexNode v4 = new VertexNode(2, 4, null);
vexList = new ArrayList<>();
vexList.add(v0);
vexList.add(v1);
vexList.add(v2);
vexList.add(v3);
vexList.add(v4);
}
进行拓扑排序,使用栈存入入度为0的顶点,每一个顶点出栈后判定其临界点是否入度为0 ,递归循环直到栈为空,代码如下:
public boolean topologicalSort() {
int count = 0;//统计输出数
Stack<Integer> stack = new Stack<>();//建栈存储入度为0的顶点
for (int i = 0;i < vexList.size(); i++) {
vexList.get(i).setIn(0);
}
for (int i = 0;i < vexList.size(); i++) {
EdgeNode edge = vexList.get(i).getFirstEdge();
while (edge != null) {
VertexNode vex = vexList.get(edge.getAdjvex());
vex.setIn(vex.getIn() + 1);
edge = edge.getNext();
}
}
//将入度为0 的顶点入栈
for (int i = 0;i < vexList.size(); i++) {
if (vexList.get(i).getIn() == 0) {
stack.push(i);
}
}
while (!stack.isEmpty()) {
//栈顶 顶点出栈
int vexIndex = stack.pop();
System.out.print(vexIndex+1 + " ");
count++;
//从顶点表结点中取出第一个边表结点
EdgeNode edge = vexList.get(vexIndex).getFirstEdge();
while (edge != null) {
int adjvex = edge.getAdjvex();
VertexNode vex = vexList.get(adjvex);
//将此 顶点的入度减一
vex.setIn(vex.getIn() - 1);
//此顶点的入度为零则入栈,以便于下次循环输出
if (vex.getIn() == 0) {
stack.push(adjvex);
}
edge = edge.getNext();
}
}
if (count != vexList.size())
return false;
else
return true;
}
(四)最小生成树:基于邻接链表的图,每次对边类的权值进行判定。重新写一个边类,之前的不满足权,代码如下:
//重写的边类
class Edge{
int v; //边的权值
int[] ConnectPoint = new int[2]; //边所连接的点
int isSelect; //是否被选择,1表示被选,0表示没有被选
char No; //图的编号,a,b,c,d...在创建图的时候初始化的
}
//构图
public class LittleTree {
public void createTree(){
Scanner in=new Scanner(System.in);
System.out.println("请输入图有几条边和几个点:");
int n=in.nextInt();
int m=in.nextInt();
Edge edge[] = new Edge[n];
System.out.println("请输入边的权值、关联点1、关联点2:");
for(int i=0;i<n;i++){
edge[i] = new Edge();
edge[i].v = in.nextInt();
edge[i].ConnectPoint[0] = in.nextInt();
edge[i].ConnectPoint[1] = in.nextInt();
edge[i].No = (char) ('a' + i);
}
sort(edge);
int hasSelectPoint[] = new int[2*m];
//权值排序之后开始选边
int j=0;
int step = 1;//选的边数,开始选第一条边
for(int i=0;i<n;i++){
//最小生成树要选的边数等于顶点数-1,那么开始要选m-1最后一条边时这样选。再break退出
if(step == m-1 && allInSelectPoint(edge[i],hasSelectPoint)){ //最后一条边了
edge[i].isSelect = 1;//直接选择
break;
}else if(edge[i].isSelect ==0 && !allInSelectPoint(edge[i],hasSelectPoint)){ //如果边没有被选,并且这条边的两个顶点不同时在顶点的数组里
edge[i].isSelect = 1;
hasSelectPoint[j] = edge[i].ConnectPoint[0];
j++;
hasSelectPoint[j] = edge[i].ConnectPoint[1];
j++;
step++; //开始选第二条边
}
}
//打印所选的边
int sum = 0; // 计算权值
System.out.print("所选的边为:");
for(int i=0;i<n;i++){
if(edge[i].isSelect==1){
sum = sum + edge[i].v;
System.out.print(edge[i].No + " ");
}
}
System.out.println();
System.out.println("权值为: " + sum);
}
private static boolean allInSelectPoint(Edge edge, int[] hasSelectPoint) {
int flag1 = 0;
int flag2 = 0;//这两个变量是分别看边的两个端点在不在存放已经选择点的数组里面
for(int i=0;i<hasSelectPoint.length;i++){
if(edge.ConnectPoint[0] ==hasSelectPoint[i]){
flag1 = 1;
}
if(edge.ConnectPoint[1] ==hasSelectPoint[i]){
flag2 = 1;
}
}
if(flag1 ==1 && flag2 ==1){ //两个点都在
return true;
}else { //都不在或者有一个点不在
return false;
}
}
//将权值进行交换
private static void sort(Edge[] edge) {
Edge tempEdge = null;
for(int i=0;i<edge.length;i++){
for(int j=i+1;j<edge.length;j++){
if(edge[j].v<edge[i].v){
tempEdge = edge[i];
edge[i] = edge[j];
edge[j] = tempEdge;
}
}
}
}
(五)最短路径:使用abcde字母分别表示几个边,完成基于无向图和有向图的最短路径查找,代码如下:
import java.util.LinkedList;
import java.util.Queue;
public class GraphByMatrix {
public static final boolean UNDIRECTED_GRAPH = false;//无向图标志
public static final boolean DIRECTED_GRAPH = true;//有向图标志
public static final boolean ADJACENCY_MATRIX = true;//邻接矩阵实现
public static final boolean ADJACENCY_LIST = false;//邻接表实现
public static final int MAX_VALUE = Integer.MAX_VALUE;
private boolean graphType;
private boolean method;
private int vertexSize;
private int matrixMaxVertex;
//存储所有顶点信息的一维数组
private Object[] vertexesArray;
//存储图中顶点之间关联关系的二维数组,及边的关系
private int[][] edgesMatrix;
// 记录第i个节点是否被访问过
private boolean[] visited;
public GraphByMatrix(boolean graphType, boolean method, int size) {
this.graphType = graphType;
this.method = method;
this.vertexSize = 0;
this.matrixMaxVertex = size;
if (this.method) {
visited = new boolean[matrixMaxVertex];
vertexesArray = new Object[matrixMaxVertex];
edgesMatrix = new int[matrixMaxVertex][matrixMaxVertex];
//对数组进行初始化,顶点间没有边关联的值为Integer类型的最大值
for (int row = 0; row < edgesMatrix.length; row++) {
for (int column = 0; column < edgesMatrix.length; column++) {
edgesMatrix[row][column] = MAX_VALUE;
}
}
}
}
//计算一个顶点到其它一个顶点的最短距离
public void Dijkstra(Object obj) throws Exception {
Dijkstra(getVertexIndex(obj));
}
public void Dijkstra(int v0) {
int[] dist = new int[matrixMaxVertex];
int[] prev = new int[matrixMaxVertex];
//初始化visited、dist和path
for (int i = 0; i < vertexSize; i++) {
//一开始假定取直达路径最短
dist[i] = edgesMatrix[v0][i];
visited[i] = false;
//直达情况下的最后经由点就是出发点
if (i != v0 && dist[i] < MAX_VALUE)
prev[i] = v0;
else
prev[i] = -1; //无直达路径
}
//初始时源点v0∈visited集,表示v0 到v0的最短路径已经找到
visited[v0] = true;
// 下来假设经由一个点中转到达其余各点,会近些,验证之
// 再假设经由两个点中转,会更近些,验证之,.....
// 直到穷举完所有可能的中转点
int minDist;
int v = 0;
for (int i = 1; i < vertexSize; i++) {
//挑一个距离最近经由点,下标装入 v
minDist = MAX_VALUE;
for (int j = 0; j < vertexSize; j++) {
if ((!visited[j]) && dist[j] < minDist) {
v = j; // 经由顶点j中转则距离更短
minDist = dist[j];
}
}
visited[v] = true;
/*顶点v并入S,由v0到达v顶点的最短路径为min.
假定由v0到v,再由v直达其余各点,更新当前最后一个经由点及距离*/
for (int j = 0; j < vertexSize; j++) {
if ((!visited[j]) && edgesMatrix[v][j] < MAX_VALUE) {
if (minDist + edgesMatrix[v][j] <= dist[j]) {
//如果多经由一个v点到达j点的 最短路径反而要短,就更新
dist[j] = minDist + edgesMatrix[v][j];
prev[j] = v; //经由点的序号
}
}
}
}
for (int i = 1; i < matrixMaxVertex; i++) {
System.out.println("**" + vertexesArray[v0] + "-->" +vertexesArray[i] + " 的最短路径是:" + dist[i]);
}
}
//获取顶点值在数组里对应的索引
private int getVertexIndex(Object obj) throws Exception {
int index = -1;
for (int i = 0; i < vertexSize; i++) {
if (vertexesArray[i].equals(obj)) {
index = i;
break;
}
}
if (index == -1) {
throw new Exception("没有这个值!");
}
return index;
}
/**
* 单源最短路径算法,用于计算一个节点到其他!!所有节点!!的最短路径
*/
public void Dijkstra2(int v0) {
// LinkedList实现了Queue接口 FIFO
Queue<Integer> queue = new LinkedList<Integer>();
for (int i = 0; i < vertexSize; i++) {
visited[i] = false;
}
//这个循环是为了确保每个顶点都被遍历到
for (int i = 0; i < vertexSize; i++) {
if (!visited[i]) {
queue.add(i);
visited[i] = true;
while (!queue.isEmpty()) {
int row = queue.remove();
System.out.print(vertexesArray[row] + "-->");
for (int k = getMin(row); k >= 0; k = getMin(row)) {
if (!visited[k]) {
queue.add(k);
visited[k] = true;
}
}
}
}
}
}
private int getMin( int row) {
int minDist = MAX_VALUE;
int index = 0;
for (int j = 0; j < vertexSize; j++) {
if ((!visited[j]) && edgesMatrix[row][j] < minDist) {
minDist = edgesMatrix[row][j];
index = j;
}
}
if (index == 0) {
return -1;
}
return index;
}
public boolean addVertex(Object val) {
assert (val != null);
vertexesArray[vertexSize] = val;
vertexSize++;
return true;
}
public boolean addEdge(int vnum1, int vnum2, int weight) {
assert (vnum1 >= 0 && vnum2 >= 0 && vnum1 != vnum2 && weight >= 0);
//有向图
if (graphType) {
edgesMatrix[vnum1][vnum2] = weight;
} else {
edgesMatrix[vnum1][vnum2] = weight;
edgesMatrix[vnum2][vnum1] = weight;
}
return true;
}
}
(六)运行结果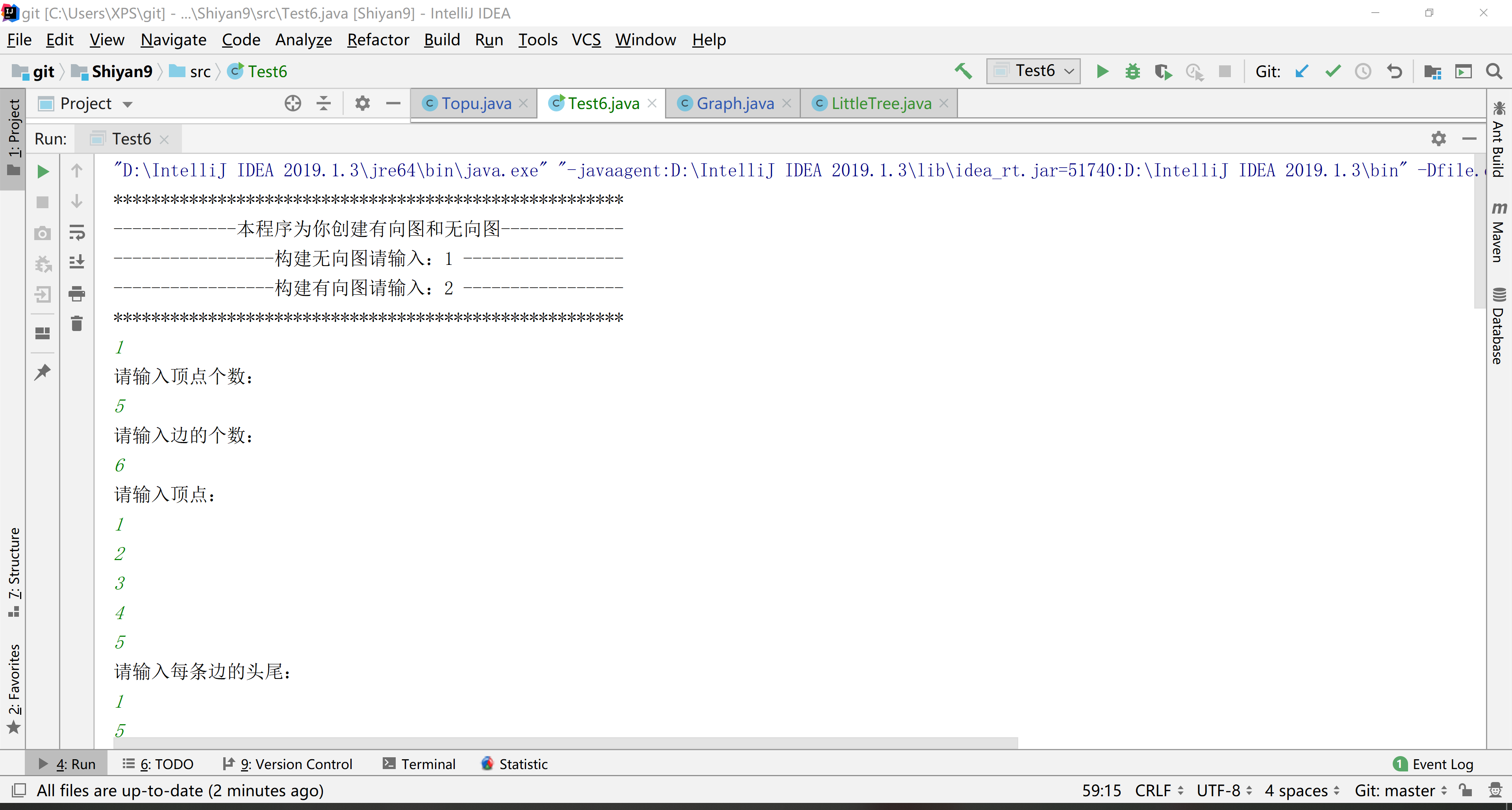
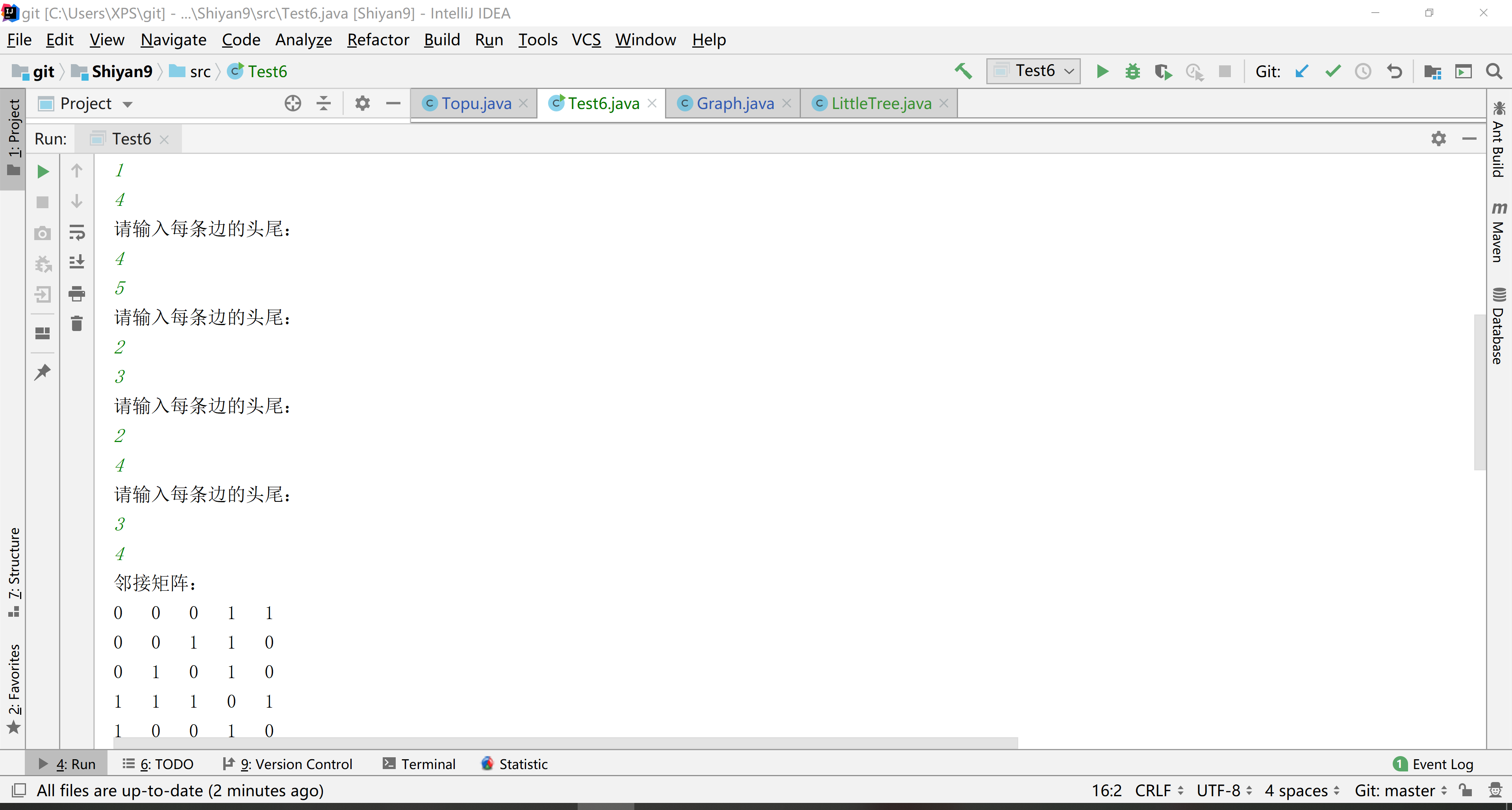
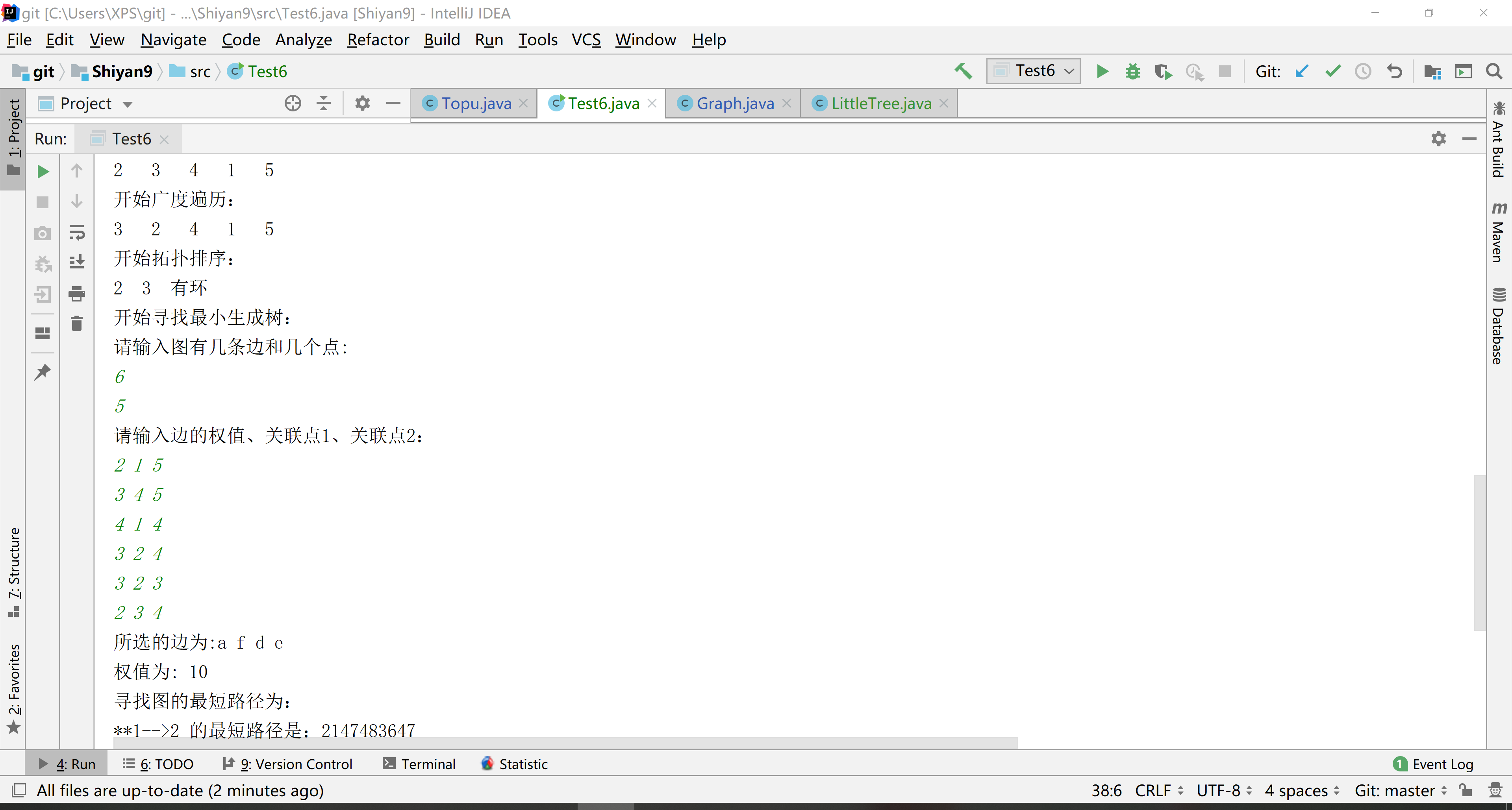
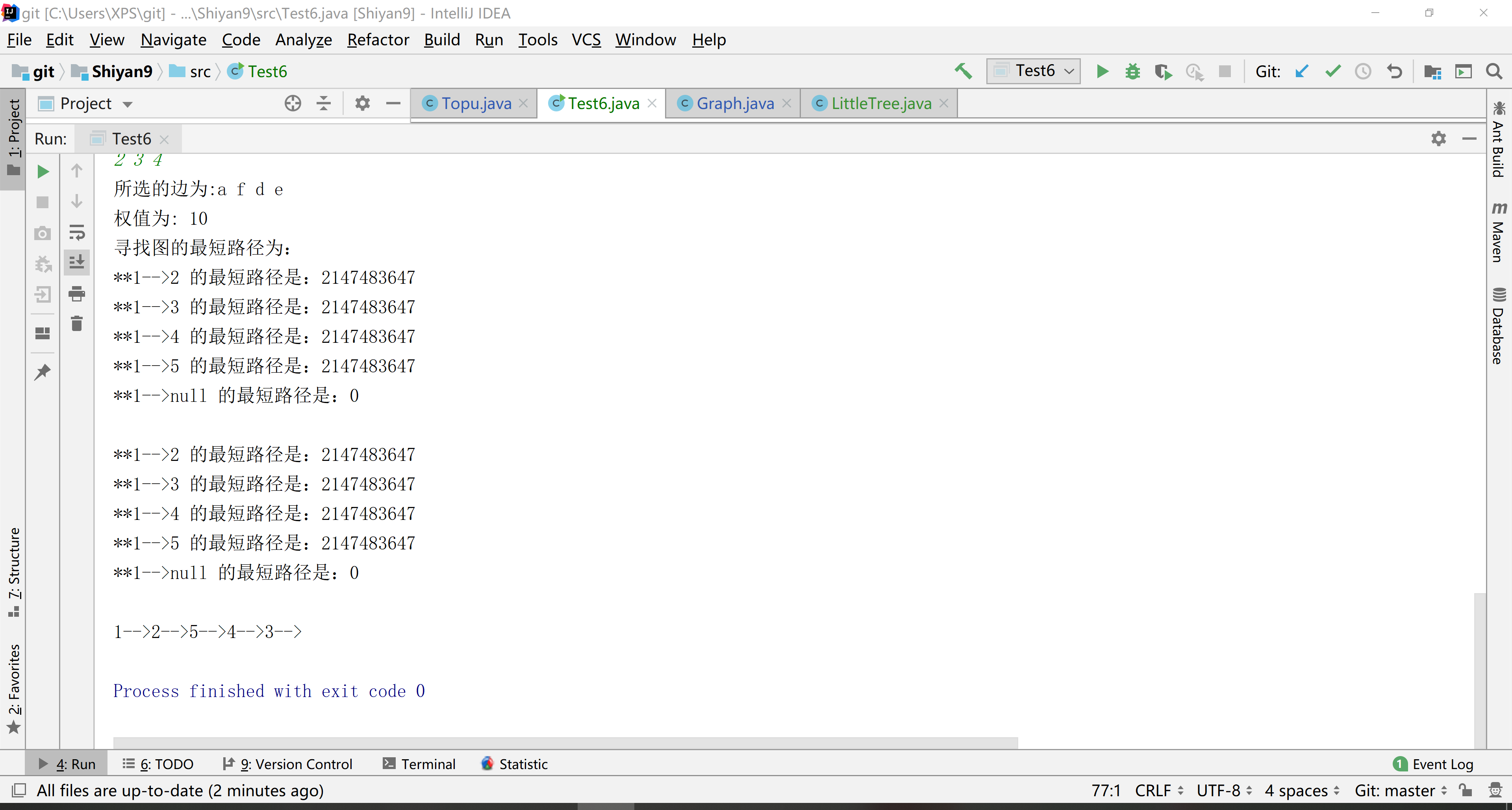
3. 实验过程中遇到的问题和解决过程
- 问题1:关于根据顶点的名字获取顶点在顶点数组中的位置和边上的位置,每次使用遍历的方法去找太麻烦了,有没有简便的方案?
- 问题1解决方案:按照顶点的下标设置顶点的名字, 比如V1在顶点数组(char[])中存为‘1’,查找在数组中的下标时,直接使用char[i]-'0'即可。
来源:https://www.cnblogs.com/lengchong/p/12003837.html