SARSA算法解决“有风的网格世界”问题
问题描述
一个有起始状态S和终止状态G的网格世界,在经过中间一段区域时,会有向上的风,风力强度如下标所示。0代表无风,1代表会被吹上去一格,2代表会被吹上去两格。
现在的目的是,从起始位置S想办法到达终点位置G,选择的动作可以是八个方向的(上、下、左、右、左上、左下、右上、右下)。这是一个标准的分幕式任务,在到达目标前,每一步的回报都是 -1。
我们的任务是采用 - 贪心策略得到在200幕的情况下,得到从S到G累计步数的增长情况。
贪心参数 epsilon = 0.1,步长参数 alpha = 0.5 ,折扣系数 gamma = 0.9 ,初始状态所有Q(s,a)= 0。
问题解决
动作数字化
动作:up down left right left-u left-down right-u right-d
动作:0 1 2 3 4 5 6 7
状态数字化
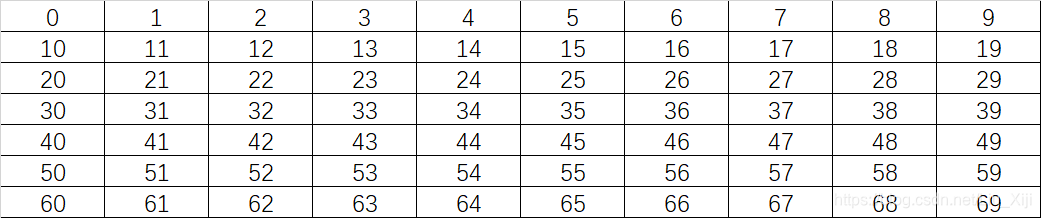
数字化后,状态-动作值函数的初始化就简单了,之后就是写算法了。
算法
经典的SARSA算法,编程时稍加修改。
程序
# _*_ coding : UTF-8 _*_
# 开发团队 : 一只猫
# 开发人员 : Jiang H.T
# 开发时间 : 2019/12/19 9:00
# 文件名称 : Sarsa_wind.py
# 开发工具 : PyCharm
import random
import xlsxwriter
alpha = 0.5 #步长
gamma = 0.9 #折扣系数
action_s = -1 #动作选择
R = []
global Q
Q = {}
for s in range(70): #字典初始化Q(s,a)的值
for a in range(8):
Q[(s, a)] = 0.0
#动作:up down left right left-u left-down right-u right-d
#动作:0 1 2 3 4 5 6 7
workbook = xlsxwriter.Workbook('D:\RL\Grid_Sarsa.xlsx') # 创建一个Excel文件
worksheet = workbook.add_worksheet('Sheet1') # 创建一个sheet
worksheet.write(0, 0, '幕数') # 创建表格标题
worksheet.write(0, 1, '累计步数')
'''
函数功能:策略选择函数
输入:状态state 、贪心参数epsilon
输出:执行的动作action
'''
def epsilon_greedy(state, epsilon):
action_m = [-10, 10, -1, 1, -11, 9, -9, 11] # state周围可能执行的动作,0表示不可能执行
action_recognition = -1
max = -10000
#边角特殊情况处理
if state == 0:
action_m[0] = 0
action_m[2] = 0
action_m[4] = 0
action_m[5] = 0
action_m[6] = 0
if state == 9:
action_m[0] = 0
action_m[3] = 0
action_m[4] = 0
action_m[6] = 0
action_m[7] = 0
if state == 60:
action_m[1] = 0
action_m[2] = 0
action_m[4] = 0
action_m[5] = 0
action_m[7] = 0
if state == 69:
action_m[1] = 0
action_m[3] = 0
action_m[5] = 0
action_m[6] = 0
action_m[7] = 0
if state == 10 or state == 20 or state == 30 or state == 40 or state == 50:
action_m[2] = 0
action_m[4] = 0
action_m[5] = 0
if state == 19 or state == 29 or state == 39 or state == 49 or state == 59:
action_m[3] = 0
action_m[6] = 0
action_m[7] = 0
if state >= 1 and state <= 8:
action_m[0] = 0
action_m[4] = 0
action_m[6] = 0
if state >= 61 and state <= 68:
action_m[1] = 0
action_m[5] = 0
action_m[7] = 0
#策略选择
rand_value = random.uniform(0, 1)
if rand_value < epsilon: #生成随机数,大于epsilon,随机选择选择
rand_value = random.randint(0, 7)
action_s = action_m[rand_value]
action_recognition = rand_value
else: #小于epsilon,值函数最大的动作
for it in range(8):
if max < Q[(state, it)]:
max = Q[(state, it)]
action_s = action_m[it]
action_recognition = it
return action_s, action_recognition
'''
函数功能:Sarsa算法执行函数
输入:
输出:执行幕数、累计执行步数
'''
def SARAS():
loop_num = 0 # 幕数
step_num = 0 #累计步数
while loop_num <= 2000: #对每幕循环
step = 0
loop_num = loop_num + 1
worksheet.write(loop_num, 0, str(loop_num))
State = 30
action_s, Action = epsilon_greedy(State, 0.1) #选策略
while True: #对幕中每一步循环
step = step + 1 #执行步数+1
nextState = State + action_s
#此部分是增加了nextState到达有风吹的区域,对nextState的调整
if str(nextState).endswith('3') or str(nextState).endswith('4') \
or str(nextState).endswith('5') or str(nextState).endswith('8'):
if nextState != 3 and nextState != 4 and nextState != 5 and nextState != 8:
nextState = nextState - 10
if str(nextState).endswith('6') or str(nextState).endswith('7'):
if nextState != 6 and nextState != 7 and nextState != 16 and nextState != 17:
nextState = nextState - 20
if nextState == 16 or nextState == 17:
nextState = nextState - 10
#核心部分
if nextState != 37:
Reward = -1
action_s, nextAction = epsilon_greedy(nextState, 0.1)
Q[(State, Action)] = Q[(State, Action)] + \
alpha*(Reward + gamma*Q[(nextState, nextAction)] - Q[(State, Action)])
else:
break
State = nextState
Action = nextAction
step_num = step_num + step
worksheet.write(loop_num, 1, str(step_num))
'''
函数功能:主函数
'''
if __name__ == '__main__':
SARAS()
workbook.close()
程序说明:不想说了,对照算法注释自己看吧,看不懂我也没办法。
数据
简单地看一下采集到的数据。
仿真
# _*_ coding : UTF-8 _*_
# 开发团队 : 一只猫
# 开发人员 : Jiang H.T
# 开发时间 : 2019/12/19 19:08
# 文件名称 : Sarsa_w_data.py
# 开发工具 : PyCharm
import pandas as pd
import matplotlib.pyplot as plt
aa = 'D:\RL\Grid_Sarsa.xlsx'
df = pd.DataFrame(pd.read_excel(aa))
df = df.set_index('累计步数')
df = df[['幕数']]
df.plot(secondary_y = [], grid=True)
plt.legend(('幕数',), loc='upper right')
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.savefig("D:\RL\Grid_Sarsa.png", dpi = 500)
plt.show()
画图分析
1.将幕数定为200,图如下:可以很清晰地看出,刚开始每幕从起始状态S到终止状态G需要更多的步数,曲线比较平滑。随着算法的学习,每幕从起始状态S到终止状态G需要的步数逐渐减少,曲线变的越来越陡峭。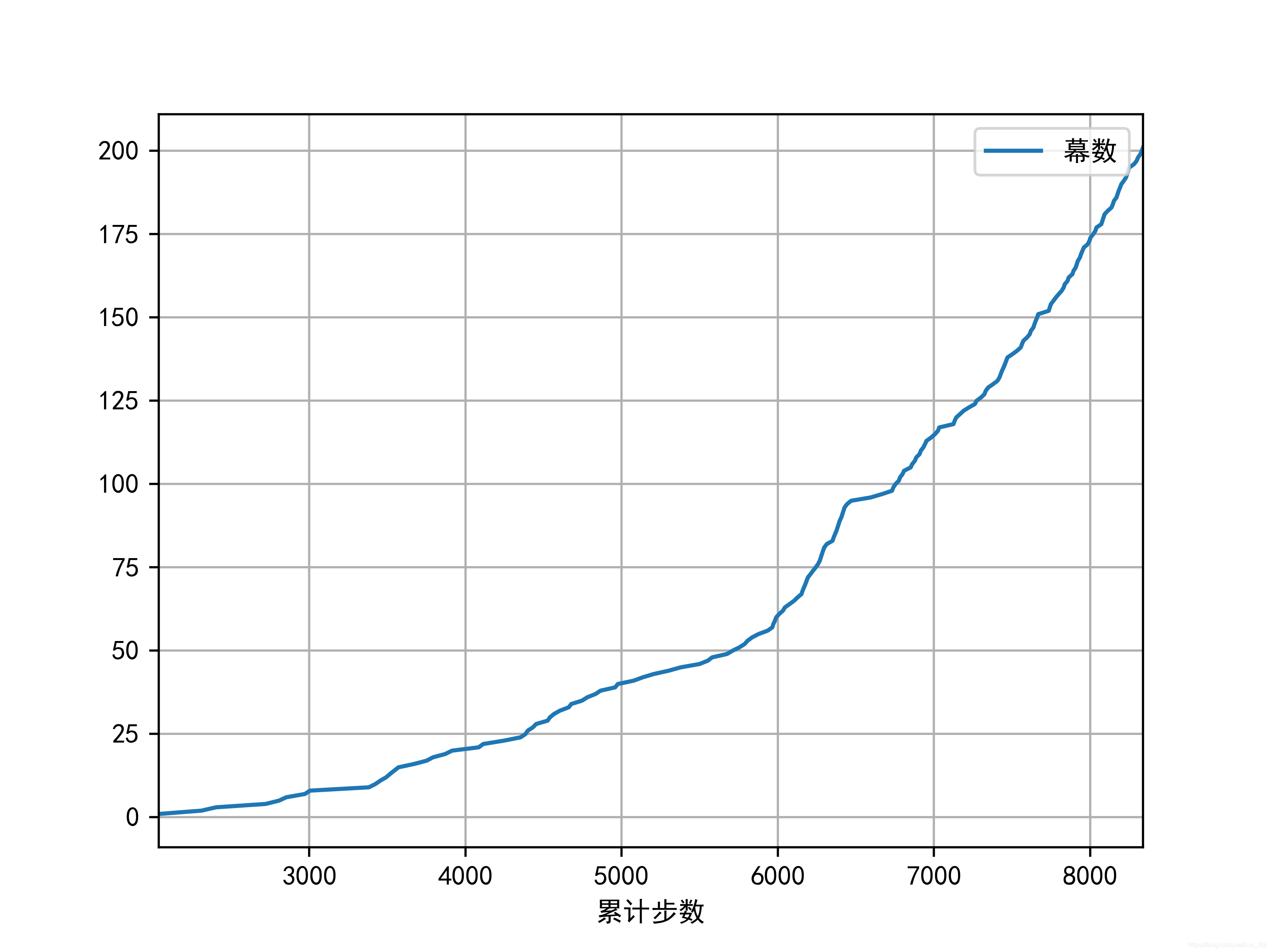
2.将幕数定为2000,图如下:发现了一个很有趣的现象,300幕以内,SARSA算法确实起到了优化效果。300幕到1100幕和1100幕到2000幕之间出现了不太一样的变化:先是每幕的步数增加**(不清楚原因)**,表现为曲线平滑,然后又开始了减少,表现为曲线陡峭。相当于在2000幕内,出现了3次优化。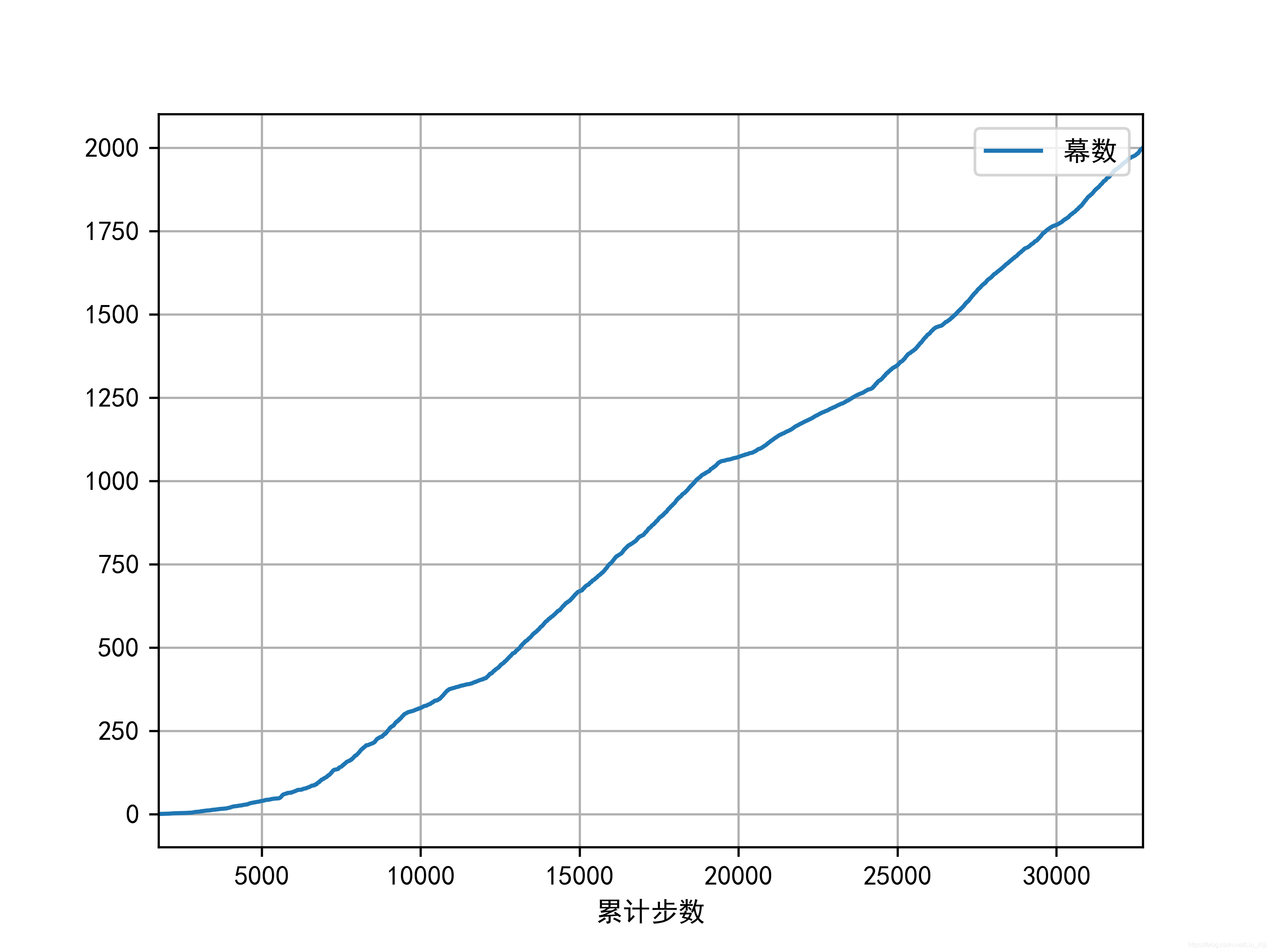
参考文献
[1]: Reinforcement Learning: An Introduction(Second Edition), Richard S. Sutton and Andrew G. Barto , 2019.9
ps:转载请表明出处
来源:CSDN
作者:柳希及
链接:https://blog.csdn.net/Liu_Xiji/article/details/103628588


