迪杰斯特拉算法求最短路径

迪杰斯特拉算法求最短路径：

(针对从某一源点到其余各顶点间的最短距离)

初步的思想过程：
1.引进两个集合S和T，指定起始点O。S用来记录已求出的最短路径的顶点(以及相应的最短路径长度)，T用来记录未求出最短路径的顶点(以及该顶点到起点O的距离)。
2. 首先，S中包含起点O；T包含除O之外的外的其他顶点，T中顶点的距离为"起点O到该顶点的距离"。如果说O点和M点不相邻，则(O,M)的距离为∞。
3. 从T中选出距离最短的顶点N，将其加入S中，并从T中移去顶点N。
4. 更新T中各个顶点到起点O的距离。之所以更新U中顶点的距离，是由于上一步中确定了N是求出最短路径的顶点，从而可以利用N来更新其它顶点的距离；例如，(O,M)的距离可能大于(O,N)+(N,M)的距离。
5. 重复3和4，直到所有顶点均被遍历。

举例说明：（例如从顶点D出发，求其到其他定点的最短路径）
在这里插入图片描述

将顶点D加入到S中：

此时，S={D(0)}, T={A(∞),B(∞),C(3),E(4),F(∞),G(∞)}。注:C(3)表示C到起点D的距离是3。
将顶点C加入到S中：

上一步操作之后，T中顶点C到起点D的距离最短；因此，将C加入到S中，同时更新U中顶点的距离。以顶点F为例，之前F到D的距离为∞；但是将C加入到S之后，F到D的距离为9=(F,C)+(C,D)。
此时，S={D(0),C(3)}, T={A(∞),B(23),E(4),F(9),G(∞)}。
将顶点E加入到S中：

上一步操作之后，T中顶点E到起点D的距离最短；因此，将E加入到S中，同时更新U中顶点的距离。还是以顶点F为例，之前F到D的距离为9；但是将E加入到S之后，F到D的距离为6=(F,E)+(E,D)。
此时，S={D(0),C(3),E(4)}, T={A(∞),B(23),F(6),G(12)}。
将顶点F加入到S中：

此时，S={D(0),C(3),E(4),F(6)}, T={A(22),B(13),G(12)}。
将顶点G加入到S中：

此时，S={D(0),C(3),E(4),F(6),G(12)}, T={A(22),B(13)}。
将顶点B加入到S中：

此时，S={D(0),C(3),E(4),F(6),G(12),B(13)}, T={A(22)}。
将顶点A加入到S中：
此时，S={D(0),C(3),E(4),F(6),G(12),B(13),A(22)}。
此时，起点D到各个顶点的最短距离就计算出来了：A(22) B(13) C(3) D(0) E(4) F(6) G(12)。

两种最常见的最短路径问题：一种是求某个源点到其余各个顶点的最短路径，另一种是求每一对顶点之间的最短路径。
一：从某个源点到其余各点的最短路径

接下来将讨论单源点的最短路径问题:给定带权有向图G和源点v0,求从v0到G中其余各顶点的最短路径。迪杰斯特拉(Dijkstra)提出了一个按路径长度递增的次序产生最短路径的算法，称为迪杰斯特拉算法。

迪杰斯特拉算法的求解过程
对于网N=(V,E)，将N中的顶点分成两组:
第一组S:已求出的最短路径的终点集合(初始时只包含源点v0)。
第二组V-S:尚未求出的最短路径的顶点集合(初始时为V- {v0})。
算法将按各顶点与v0间最短路径长度递增的次序，逐个将集合V-S中的顶点加入到集合S中去。在这个过程中，总保持从v0到集合S中各顶点的路径长度始终不大于到集合V- S中各顶点的路径长度。

假设用带权的邻接矩阵arcs来表示带权有向网G, G.arcs[i][j]表示弧<vi, vj>上的权值。若<vi,vj>不存在，则置G.arcs[i][j] 为∞，源点为v0。

算法的实现要引入以下辅助的数据结构。

①一维数组S[i]:记录从源点v0到终点vi是否已被确定最短路径长度，true 表示确定，false表示尚未确定。
②一维数组Path[i];记录从源点v0到终点vi的当前最短路径上的直接前驱顶点序号。初值为:如果从v0到vi有弧，则Path[i]为v0;否则为-1。
③一维数组D[i]:记录从源点v0到终点vi的当前最短路径长度。其初值为:如果从v0到vi有弧，则D[i]为弧上的权值;否则为∞。

显然，长度最短的一条最短路径必为(v0 vk)，满足以下条件:D[k]= Min{D[i]|vi∈V-S}

求得顶点的最短路径后，将其加入到第一组顶点集S中。
每当加入一个新的顶点到顶点集S,对第二组剩余的各个顶点而言，多了一个“中转”顶点，从而多了一一个“中转”路径，所以要对第二组剩余的各个顶点的最短路径长度进行更新。
原来v0到vi的最短路径长度为D[i]。加进vk之后，以vk作为中间顶点的“中转”路径长度为: D[k]+G.arcs[k][i]
若D[k]+ G.arcs[k][i]<D[i] ,则用D[k]+ G.arcs[k][i]取代D[i]。

更新后，再选择数组D中值最小的顶点加入到第一组顶点集S中，如此进行下去，直到图中所有顶点都加入到第一组顶点集S中为止。

迪杰斯特拉算法[算法步骤]

①初始化:

将源点v0加到S中，即S[v0]= true;
将v0到各个终点的最短路径长度初始化为权值，即D[i]+ G.arcs[v0][vi]，(vi∈V-S);
如果v0和顶点vi之间有弧，则将vi的前驱置为v0,即Path[i]=v0,否则Path[i]=-1。

②循环n-1次，执行以下操作:

选择下一条最短路径的终点vk，使得:
D[k]= Min{D[i]|vi∈V-S}将vk加到S中，即S[vk]=true;
根据条件更新从v0 出发到集合V-S上任一项点的最短路径的长度，若条件D[k]+ G.arcs[k][i]<D[i]成立，则更新D[i]=D[k]+ G.arcs[k][i]同时更改vi的前驱为vk; Path[i]=k。

迪杰斯特拉算法[算法描述]

void ShortestPath_DIJ(AMGraph G, int v0)
{//Dijkstra算法求有向网G的v0顶点到其余顶点的最短路径
n=G.vexnum;//n为G中顶点的个数
for(v=0;v<n;++v)//n个顶点依次初始化
{
    S[v]=false;//S初始化为空集
    D[v]=G.arcs[v0][v];//将v0到各个终点的最短路径长度初始化为弧上的权值
    if(D[v]<MaxInt)  Path[v]=v0;//如果v0和vi之间有弧，则将v的前驱置为v0 
    else Path[v]=-1;//如果v0和vi之间无弧，则将v的前驱置为-1

}
S[v0]=true;//将v0加入S 
D[v0]=0;//源点到源点的距离为0
/******初始化结束，开始主循环，每次求得v0到某个顶点v的最短路径，将v加入到S集******/
for(i=1;i<n;++i)//对其余n-1个顶点，依次j进行计算
{
    min=MaxInt;
    for(w=0;w<n;++w)
        if(!S[w]&&D[w]<min)//如果最短路径没有被找到
       {
           v=w;//选择一条当前的最短路径，终点为v
           min=D[w];
        }
    S[v]=true;//将v加入到S中
    for(w=0;w<n;w++)//更新从v0出发到集合V-S上所有顶点的最短路径长度
        if(!S[w]&&D[v]+G.arcs[v][w]<D[w])
    {
        D[W]=D[v]+D.arcs[v][w];//更新D[w]
        path[w]=v;//更改w的前驱为v
    }
}

图G6：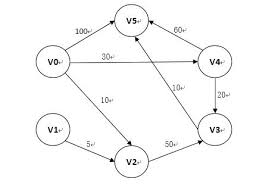
在这里插入图片描述
利用以上算法，对上述有向图求解最短路径，给出算法中各参量的初始化结果和求解过程中的变化。
**图G6：**的邻接矩阵表示为：

∞ ---- ∞ ---- 10 ---- ∞ ----30 ---- 100
∞ ---- ∞ ----- 5 -----∞ ---- ∞-------- ∞
∞ -----∞ ----- ∞ — 50 ---- ∞------ -∞
∞ ---- ∞ ------∞----- ∞----- ∞------ 10
∞ ---- ∞-------∞---- 20----- ∞------ 60
∞----- ∞------ ∞ ---- ∞------∞------- ∞

迪杰斯特拉算法初始化结果：

	v=0	v=1	v=2	v=3	v=4	v=5
S	true	false	false	false	false	false
D	0	∞	10	∞	30	100
Path	-1	-1	0	-1	0	0

迪杰斯特拉算法求解过程中各参量的变化：

在这里插入图片描述
如何从表中读取源点v0到终点v5的最短路径，以顶点v5为例：
Path[5]=3->Path[3]=4->Path[4]=0
反过来排列，得到路径0,4,3,5，这就是源点v0到v5的最短路径。

[算法分析]
迪杰斯特拉算法求解最短路径的主循环共进行n- 1次，每次执行的时间是O(n),所以算法的时间复杂度是O(n^2)。如果用带权的邻接表作为有向图的存储结构，则虽然修改D的时间可以减少，但由于在D向量中选择最小分量的时间不变.
所以时间复杂度仍为O(n^2).
人们可能只希望找到从源点到某一个特定终点的最短路径，但是，这个问题和求源点到其他所有顶点的最短路径一样复杂，也需要利用迪杰斯特拉算法来解决，其时间复杂度仍为O(n^2)。

来源：CSDN

作者：小咕咚呐

链接：https://blog.csdn.net/qq_44024359/article/details/103574892

标签

最短路径

算法