[16' KDD]Compressing Graphs and Indexes with Recursive Graph Bisection

Compressing Graphs and Indexes with Recursive Graph Bisection [SIGKDD' 16]

• Authors
• Abstract
• Intro. & Motiv.
• Algorithmic Aspect
• 定义图重排问题的优化目标
• 统一建模与新的优化目标
• 之前的一些近似算法
• Compression-friendly Graph Reordering
• 算法框架：递归二分图
• 图二分方案
• Experiments
• 数据集
• 压缩效果
• 重排后的邻接矩阵情况
• Conclusion & Inspiration

Authors

本文发表于2016年SIGKDD上，第一作者是来自卡耐基梅隆大学(CMU)的Lax Dhulipala。其与来自FaceBook的多人合作完成了本工作。原文链接

---

Abstract

图重排(Graph reordering)，顾名思义就是把图的节点序号重新排列。图重排的意义是：通过重新排列，增强图表示的结构局部性。而图表示的结构局部性含义即邻接结构上相似的顶点，在线性排列映射得到的序号能够相近。例如，原有节点集{1,2,3,4,5}，其中1和5全部都连接了2和3，图重排之后，原来编号为1和5的这两个点就会更加邻近。

很容易可以想到的是，图重排造成的图线性表示结构上结构局部性的提升，会进一步带来提升图和倒排索引(可以理解为有向图)压缩率上的重要作用，原因将在Intro.&Motiv.阶段做进一步介绍。

本工作的立足点在于优化压缩，于是从实现压缩友好的图重排技术的目标出发，设计并实现了理论上可靠的、基于递归图二分的重排算法。

实验以十亿节点、千亿边级别图为例，展示了重排后在压缩率方面的明显提升。新的方法理论简单，且支持并行和分布式实现。

---

Intro. & Motiv.

在本部分，介绍了差分实现压缩的原理，简要分析了优化差分压缩与结构局部性的关系，并提出了本工作的动机。

• 差分压缩的过程和原理：图的邻接矩阵是由(节点，节点的邻结向量)对组成的。差分压缩的过程是每个图节点的邻接向量按照其元素大小进行升序排序。除第一个节点之外，每个节点的新编码使用与前一个节点序号的差来表示。
  例如：节点v的邻接向量为[1,3,4,6,7,9,10]。差分压缩后的节点邻接向量为[1,3-1,4-3,6-4,7-6,9-7,10-9]=[1,2,1,2,1,2,1]。之后采用整数压缩方式编码差分。显然，因为向量数值减小了，使用二进制编码时明显提升了压缩率。

• 优化差分压缩与图重排、优化结构局部性的关系：差分压缩的效果取决于邻接矩阵差分的分布情况。差分越小、越规律，越有利于实现好的压缩效果。这启发我们对图序号进行重排。那么如何对图序号进行重排呢？实际上，节点的结构局部性强，正是指节点具有相似的邻接情况。将这部分节点通过重排排近，在邻接表中他们的差就会变小。结构上相似的节点，在图节点的线性表示顺序中尽可能靠近，减小差分值，是我们的优化目标。

• 工作动机：找到对图结构压缩友好的图重排方案，即通过重排图序号来实现有担保的压缩质量，并直接体现在压缩率的提升上。

• 全文贡献：
  ①模型：将图重排和文件标识符分配进行统一建模抽象，证明了求本问题的最优解是一个NP-hard level；
  ②算法：提出了对压缩友好的图重排算法；
  ③实验：实验证明，图重排后压缩率有了稳定提升。

---

Algorithmic Aspect

在本部分，首先形式化定义了图重排问题的优化目标函数，此后将图重排问题和倒排索引文档编号问题统一建模，最后总结了解决此前NP-hard问题的一些优化算法。

定义图重排问题的优化目标

图重排问题：一个组合优化问题，目标是对于每个输入的图，找到图节点的线性表示，使得某目标函数达到最优。

图节点的线性表示：现有一个图G=(V,E),n=|V|，定义一个映射π:V→{1,2,…,n}。优化目标是让(结构上)“相似”的节点在π中离得尽可能近。

• 最小线性排列(MLA,Minimum Linear Arrangement)

  $min\sum_{(u,v)\in E}|\pi(u)-\pi(v)|$

• 最小对数排列(MLOGA,Minimum Logarithmic Arrangement)

  $\min \sum_{(u,v)\in E}log|\pi(u)-\pi(v)|$

• 最小对数间距排列(MLOGGAPA,Minimum Logarithmic Gap Arrangement)

首先定义一个节点邻结点的编码长度： $f_{\pi}(v,out(v))=\sum_{i=1}^{k-1}log|\pi(v_{i+1})-\pi(v_{i})|$

MLOGGAPA的优化目标是：

$\sum_{v\in V}f_{\pi}(v,out(v))$

MLOGA 和 MLOGGAPA是同时被引入的，在Chierichetti等人的工作中，他们展示了MLOGA是NP-hard问题，并没有分析 MLOGGAPA的复杂度。本文的贡献之一是证明了 MLOGGAPA 也是一个 NP-hard问题，在这里不再赘述。

统一建模与新的优化目标

此前工作没有将图重排问题文档id分配问题统一建模，但实际上DIA是一个有向图。本文将两个问题统一建模。

统一建模：将节点划分为查询节点集(Q)和数据节点集(D)，形成一个二分图。在图模型下，查询节点即邻接矩阵的索引节点值，数据节点即为索引节点对应的邻接向量；在索引模型下，查询节点即为关键词，数据节点即为对应的文章集。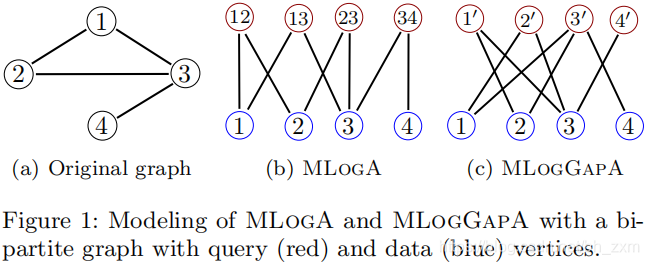
新的优化目标：形式上来说，令G=(Q∪D，E)为无向无权二分图，其中|D|=n,|E|=m。目标是找到一个D的排列，使得：

$min \sum_{q\in Q}\sum_{i=1}^{deg_{q}-1}log(\pi(u_{i+1})-\pi(u_i))$

目标函数的值的建立与最小化压缩存储位数有密切关系，将这个优化目标叫BIMLOGA。

之前的一些近似算法

本部分列举了解决解决MLA，MLOGA,MLOGGAP等的近似算法，通过近似算法达到了局部最优解。文章接下来将集中设计一个解决BIMLOGA问题的重排近似算法。

---

Compression-friendly Graph Reordering

输入：无向二部图G=(Q∪D,E)
目标：计算D的顺序

算法框架：递归二分图

本算法通过递归二分原图，递归的每一步找到子图的线性排列，实现图重排。最重要的步骤是在每步递归时图二分的方案。整个算法的框架如下：

图二分方案

首先，对于图G随机产生一个平均分配，将D划分为V1和V2，并且定义一个cost函数。

第二，对于每一个D中的节点v，计算其移动到另一个集合时cost函数的值，并与现在的cost函数作差，得到gain[v]。

第三，将V1、V2中的gain按照降序排序，对于每个节点，如果gain[v]+gain[u]>0，则交换v和u。

第四，重复二、三步，直到没有可以交换的点对或者达到了迭代次数上限。

最后，返回D的分配V1和V2。

算法详情如下：

在以上的二分方案中，实际上是在最小化loss函数，这个cost函数的设计是基于BIMLOGA的，用以下的函数式来定义：

$\sum_{q\in Q}(deg_{1}(q)log(\frac {n_{1}}{deg_{1}(q)+1})+deg_2(q)log(\frac{n_2}{deg_2(q)+1}))$

这个目标函数估计了表示用delta编码方式编码图G需要的比特数。其解释如下图：

---

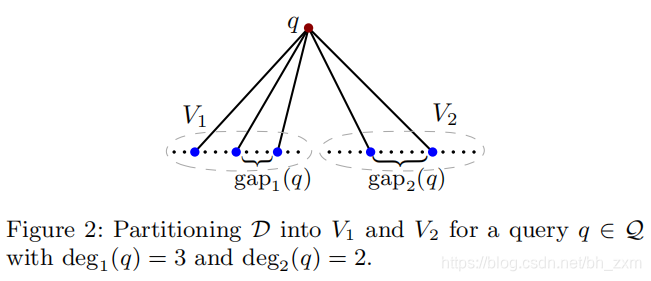
Experiments

在实验阶段，文章按照两个方面做了分析。第一，是对于这种算法(BP)的一些参数的讨论，包括迭代深度、初始化方法；第二，是对于BP得到的压缩效果的讨论。下面的内容主要挑拣一些有启发的实验结果进行呈现。

数据集

主要包括社交网络图、倒排索引图的一些数据集。

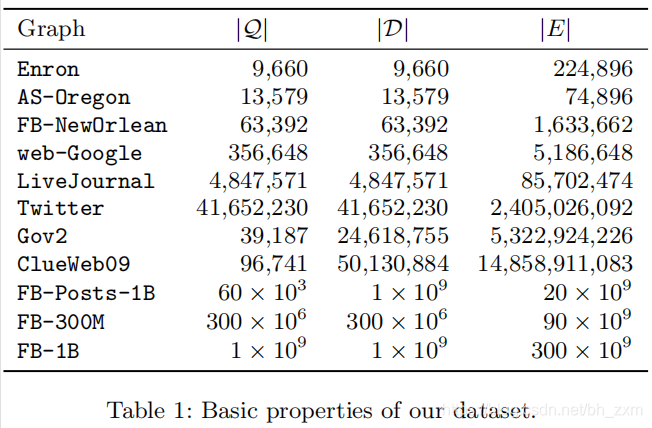
压缩效果

压缩效果提升了5%~20%，具体的数值不再列出。

重排后的邻接矩阵情况

从下图可以看出，完成重排之后，BP算法形成了一个分块结构。有的连续节点集之间的边非常少，有的则非常稠密。与图的局部特征一致，说明本方法充分挖掘了结构局部性。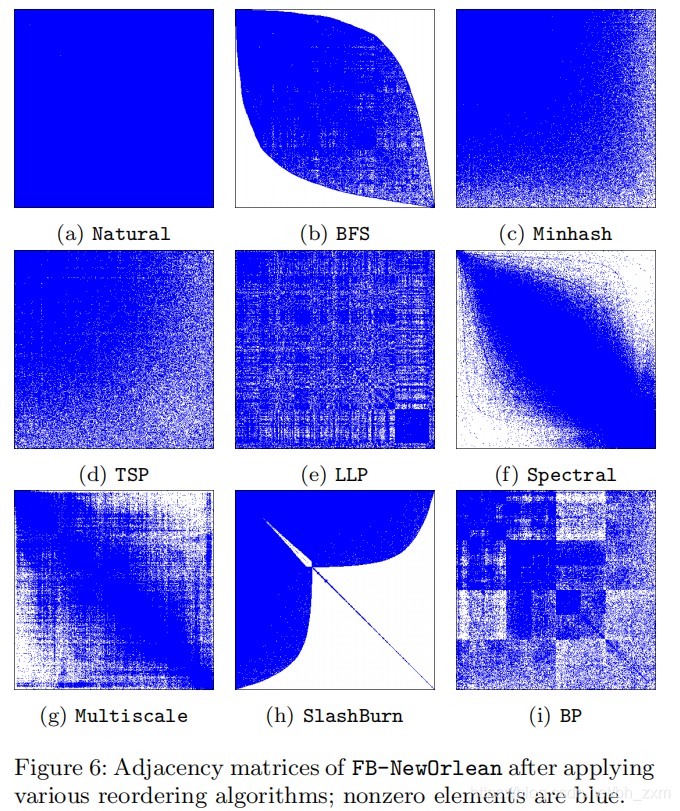

---

Conclusion & Inspiration

本文使用图重排来提升压缩效果。动机是使结构相似的节点在线性映射中尽量靠近，以减小差分。本文提出了求解该问题的基于递归图二分的、求局部最优解的近似算法。实验证明了当前算法实现了比较好的压缩效果。

有意思的是，本篇论文的立意为图压缩。为了实现图压缩，利用了重排后得到的良好的图局部特性来实现。实现方式是：直接建立与图压缩有关的cost函数，设计近似算法实现效果。实际上，最后的邻接矩阵体现了很好的局部特征，这是实现图压缩过程中得到的一个中间产物。(Figure 6)

来源：CSDN

作者：RecoderChris

链接：https://blog.csdn.net/bh_zxm/article/details/103581541