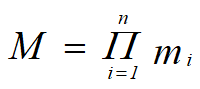一、关系数据结构
关系模型由关系数据结构，关系操作集合，关系完整性约束三部分组成
1.1关系
单一的数据结构——关系：现实世界的实体以及实体间的各种联系均用关系来表示
逻辑结构——二维表：从用户角度，关系模型中数据的逻辑结构是一张二维表
1.1.1域
定义：一组具有相同数据类型的值的集合
例如：自然数，整数，长度小于25字节的字符串集合，{1，0}等
1.1.2笛卡尔积
1、笛卡尔积
给定一组域D1，D2，…，Dn，允许其中某些域是相同的
D1，D2，…，Dn的笛卡尔积为：D1×D2×…×Dn ＝｛ (d1，d2，…，dn)｜di 
Di，i＝1，2，…，n｝
它是所有域的所有取值的一个组合，且不能重复
2、元组
笛卡尔积中每一个元素（d1，d2，…，dn）叫作一个n元组或简称元组
3、分量
笛卡尔积元素（d1，d2，…，dn）中的每一个值di 叫作一个分量
4、基数
若Di（i＝1，2，…，n）为有限集，其基数为mi（i＝1，2，…，n），则D1×D2×…×Dn的基数M为：
5、笛卡尔积的表示方法
笛卡尔积可表示为一张二维表。表中的每行对应一个元组，表中的每列对应一个域
1.1.3关系
1、关系
D1×D2×…×Dn的子集叫作在域D1，D2，…，Dn上的关系，表示为R（D1，D2，…，Dn）R：关系名，n：关系的目或度
2、元组
关系中的每个元素是关系中的元组，通常用t表示
3、单元关系与二元关系
当n=1时，称该关系为单元关系或一元关系
当n=2时，称该关系为二元关系（Binary relation）
4、关系的表示
关系也是一个二维表，表的每行对应一个元组，表的每列对应一个域
5、属性
关系中不同列可以对应相同的域
为了加以区分，必须对每列起一个名字，称为属性
n目关系必有n个属性
6、码
① 候选码
若关系中的某一属性组的值能唯一地标识一个元组，则称该属性组为候选码。简单的情况：候选码只包含一个属性
② 全码
最极端的情况：关系模式的所有属性组是这个关系模式的候选码，称为全码
③ 主码
若一个关系有多个候选码，则选定其中一个为主码（Primary key）
④ 主属性
候选码的诸属性称为主属性，不包含在任何侯选码中的属性称为非主属性或非码属性
7、三类关系
① 基本关系（基本表或基表）
实际存在的表，是实际存储数据的逻辑表示
② 查询表
查询结果对应的表
③ 视图表
由基本表或其他视图表导出的表，是虚表，不对应实际存储的数据
8、基本关系的性质
① 列是同质的
② 不同的列可出自同一个域
- 其中的每一列称为一个属性
- 不同的属性要给予不同的属性名
③ 列的顺序无所谓,，列的次序可以任意交换
④ 任意两个元组的候选码不能相同
⑤ 行的顺序无所谓，行的次序可以任意交换
⑥ 分量必须取原子值
1.2关系模式
关系模式是型，关系是值。关系模式是对关系的描述
- 元组集合的结构
- 属性构成
- 属性来自的域
- 属性与域之间的映象关系
- 完整性约束条件
关系模式可以形式化地表示为：
R（U，D，DOM，F）
R 关系名
U 组成该关系的属性名集合
D U中属性所来自的域
DOM 属性向域的映象集合
F 属性间数据的依赖关系的集
关系模式通常可以简记为 R (U) 或 R (A1，A2，…，An) R: 关系名，A1，A2，…，An : 属性名
关系模式与关系
关系模式
- 对关系的描述
- 静态的、稳定的
关系
- 关系模式在某一时刻的状态或内容
- 动态的、随时间不断变化的
二、关系的完整性
包括实体完整性，参照完整性和用户定义的完整性
实体完整性，参照完整性称为关系的两个不变性
2.1实体完整性
规则：若属性A是基本关系R的主属性，则A不能取空值。空值即“不存在”、“不知道”或“无意义”的值
例如，学生（学号，姓名，性别，专业，年龄）关系中学号是主码，则学号不能取空值
说明
- 针对基本关系而言
- 现实世界中的实体是可区分的，但它们具有某种唯一性标识
- 关系模型中以主码作为唯一性标识
- 主码中的主属性不能取空值
2.2参照完整性
外码
设F是基本关系R的一个或一组属性，但不是关系R的码；如果F与基本关系S的主码Ks相对应，则称F是R的外码，并称基本关系R为参照关系，基本关系S为被参照关系或目录关系
- 关系R和S不一定是不同的关系
- 目标关系S的主码Ks 和参照关系的外码F必须定义在同一个（或一组）域上
- 外码并不一定要与相应的主码同名
规则：若属性（或属性组）F是基本关系R的外码，它与基本关系S的主码Ks相对应（基本关系R和S不一定是不同的关系），则对于R中每个元组在F上的值必须：
- 或者取空值（F的每个属性值均为空值）
- 或者等于S中某个元组的主码值
2.3用户定义的完整性
反映特定的数据库所涉及的数据必须满足的语义约束条件。由于不存在一般性规则，这些约束条件必须由用户根据实际问题的语义指定
例如，在教务管理数据库中，我们可以定义如下约束条件：学生成绩必须是0~100的整数；学生的累积不及格课程不得超过5门等
三、关系代数
关系代数是过程化查询语言，包括的运算以一个或两个关系为对象，并产生一个新的关系作为运算结果
一些运算如并、差、交和笛卡尔积是沿用集合论关系的传统运算，另一些运算如选择、投影、连接等是为了满足数据库查询需要引进的
3.1基本运算
基本的关系运算有五种，包括选择、投影、并、差、笛卡尔积（之所以称为基本的，是因为其中任何运算都不能用其他运算表示）
3.1.1选择运算
一元运算，从给定的关系中选取满足一定条件的元组
设 R是一个关系，F是一个公式，涉及①运算对象，它们是常量或属性名②算数比较运算符＞，≥，＜，≤，＝或<>③逻辑运算符
，
，
选择
(R)是 R中使得公式 F为真的元组 t的集合：
(R) = { t | t 
R∧F( t ) } 注意：选择的结果形成一个新的关系，它与 R具有相同的属性。选择是行运算，他从表中选择满足给定条件的行
3.1.2投影运算
一元运算，给定一个关系 R，去掉其中一些属性，重新排列剩下的属性，形成一个新关系
投影
(R) = { t | ( 
u) (u 
R∧t = u[A1,...,Ak] ) }
投影是列运算，它从表中删除某些列，但可能导致删除运算结果的重复行
3.1.3并运算
关系 R和 S的并记作 R S，是属于 R，或属于 S，或属于两者的所有元素的集合
3.1.4差运算
关系 R和 S的差记作 R - S，是属于 R，但不属于 S的所有元素的集合
3.1.5笛卡尔积运算
设 R与 S分别是 n元和 m元关系。R和 S的笛卡尔积记作 RS，其每个元组的前 n个分量是关系 R的一个元组，后 m个分量是关系 S的一个元组。如果属性 A同时出现在 R和 S中，则 RS中分别用 R.A和 S.A表示以示区别
设 u=(
,...,
)，v=(
,...,
) u和v的串接记作 
，定义为
=(
,...,
,
,...,
)。所以 R
S={ t | ( 
u) ( 
v) ( u 
R∧ v 
S∧ t =
) } 3.2附加的关系运算
3.2.1交运算
关系 R和 S的交记作 R S，是既属于 R，又属于 S的所有元素的集合
3.2.2除运算
设 R的属性为 A1,...,An-m,An-m+1,...,An，S的属性为 An-m+1,...,An。关系 R和 S的除运算记作 R
S，其结果是 A1,...,An-m上的关系 关系 R
S是满足如下条件的元组集合：对于 S中的每个元组 (
,...,
)，元组 (
,...,
,
,...,
)在 R中，即属于关系 R但不属于关系 S的属性与 S中属性做笛卡尔积，筛选出 笛卡尔积的所有结果在 R中出现、属于关系 R而不属于关系 S的属性 3.2.3连接运算
设 A是关系 R的属性，B是关系 S的属性，
是算数比较运算符。关系 R和 S在属性 A和 B上的 -连接记作 R 
S，它是满足如下条件的元组的集合：存在 uR，vS使得u[A]和 v[B]满足算术比较关系 
，并且 t=
为等号时，称为等值连接 3.2.4自然连接
关系 R和 S的自然连接记作 R
S。设 R和 S的共同属性为 C1,...,Ck，R的其他属性为 A1,...,Ai，S的其他属性为 B1,...Bj，则 R
S=
( 
(RS) ) 注意：自然连接是唯一依赖于关系属性名 的运算。当 R和 S不含共同属性时，自然连接退化为笛卡尔积。自然连接和等值连接的区别：自然连接在相同属性上进行相等比较，并投影去掉重复属性；等值连接并不要求一定在相同属性上进行相等比较，也不删除重复属性
3.3用关系代数表达式表示查询
关系代数表达式形式的定义：
- 数据库中的关系和常量关系（显示给出的元组集合）是关系代数表达式
- 如果 E是关系代数表达式，则 (F) 也是
- 如果 E是关系代数表达式，，X是 E中的属性列表，则 (E) 是关系代数表达式
- 如果 E1和 E2是关系代数表达式，则由上述运算产生的仍是关系代数表达式
给出的所有关系运算中，最常用的是选择、投影、自然连接
根据下图写出关系代数
3.4扩展的关系运算
3.4.1聚集函数与分组聚集运算
聚集函数作用于一个多重集，返回单个值（多重集是允许元素重复出现的 "集合"）
分组聚集运算具有以下形式：
其中，G1,...Gk是分组属性，A1,...,Aj是聚集属性，它们都是 R的属性，f1,..., f j 是聚集函数
例如，
(SC)将对 SC的元组按学号相同分组，求每组的平均成绩 3.4.2外连接运算
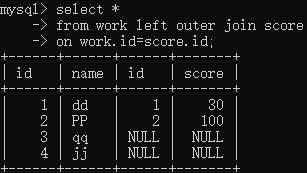
1、左外连接
左外连接是在两表进行自然连接，只把左表要舍弃的保留在结果集中，右表对应的列上填null
sql语句：Select …… from 表1 left outer join 表2 on 表1.C=表2.C
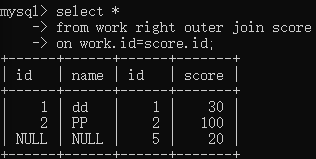
2、右外连接
右外连接是在两表进行自然连接，只把右表要舍弃的保留在结果集中，左表对应的列上填null
Select …… from 表1 rignt outer join 表2 on 表1.C=表2.C
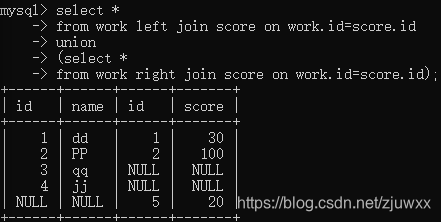
3、全外连接
全外连接是在两表进行自然连接，只把左表和右表要舍弃的都保留在结果集中，相对应的列上填null
Select …… from 表1 full join 表2 on 表1.C=表2.C
