线性排序:如何根据年龄给100W用户数据排序
桶排序、计数排序、基数排序,因为这些算法的时间复杂度是线性的,所以叫做线性排序,之所以能做到线性的时间复杂度,是因为这三个算法是基于比较的排序算法,都不涉及元素之间的比较操作
重点是掌握这些排序算法的适用场景
桶排序(bucket sort)
核心思想是将要排序的数据分到几个有序的桶里,每个桶里的数据再单独进行排序,桶内排完序之后,再把每个桶里面的数据按照顺序依次取出,组成的序列就是有序的
桶排序的时间复杂度是O(n):如果要排序的数据有n个,把它们均匀的划分到m个桶内,每个桶里就有k = n/m个元素,每个桶内部使用快排,时间复杂度为O(),m个桶就是O(),因为k=n/m,所以m个桶即整个桶的时间复杂度是O(),当桶的个数m接近数据个数n时,log(n/m)就是一个非常小的常量,桶排序的时间复杂度接近O(n)
桶排序看起来很优秀,但是不能替代之前的排序算法,因为桶排序对排序数据的要求很苛刻,首先,要排序的数据需要很容易划分成m个桶,并且,桶与桶之间有天然的大小顺序,每个桶内数据排完序之后,桶与桶之间的数据不需要进行排序,其次,数据在各个桶之间的分布是比较均匀的,如果数据在经过桶的划分之后,有些桶里的数据很多,有些桶里的数据没有,桶内的数据排序时间复杂度就不是常量级的,极端情况下,退化为O(nlogn)的排序算法
桶排序更适合外部排序中,即外部排序是数据存储在外部磁盘中,数据量比较大,内存有限,无法将数据全部加载到内存中,比如有10GB数据,希望按照订单金额进行排序,但是我们的内存有限只有几百MB,无法一次性把10GB数据加载到内存中,怎么办?
运用桶排序思想,先扫描一遍文件,看订单金额所处的数据范围,假设经过扫描得到,订单金额处于1到100000中,将所有的金额划分到100个桶里,第一个桶存储1到1000之内的订单,第二个范围是1001到2000之内的单子,每个桶对应一个文件,并按照金额范围大小顺序编号命名为(00,01,02,03……99),理想情况下,订单会被均匀划分到100个文件中,每个小文件中存储100MB的订单数据,可以将这100个小文件依次放到内存中,用快排排序,等所有文件都排好序之后,只需要按照文件编号,从小到大依次读取每个小文件中的订单数据,并将其写入到一个文件中,那这个文件中存储的就是按照金额大小从小到大的订单数据
针对划分之后还是比较大的文件可以继续划分,比如如果金额在1到1000内的比较多,将这个区间继续划分为10个小区间,1到100,101到200……901到1000,如果划分之后101到200之间的订单还是太多,就继续再划分,直到所有的文件都能读入内存为止
计数排序(Counting Sort)
计数排序其实是桶排序的一种特殊情况
当要排序的n个数据,所处的范围并不大的时候,比如最大值是k,可以把数据划分为k个桶,每个桶内的数据值都是相同的,省掉了桶内排序的时间
高考查成绩的时候,你们省有上百万考生,如何通过成绩快速排序得出名次?
考生的满分是900,最小值为0分,数据的范围很小,可以分成901个桶,对应分数从0到900,根据考生的成绩,将上百万考生划分到这901个桶,桶内的数据都是分数相同的考生,所以并不需要再进行排序,只需要依次扫描每个桶,将桶内的考生依次输出到一个数组中,实现了上百万考生的排序,因为只涉及扫描遍历操作,所以时间复杂度是O(N)
为什么叫做“计数”排序?
假设只有8个考生,分数在0到5之间,这些考生放入一个数组A[8]中,分为是2,5,3,0,2,3,0,3,考生的成绩从0到5,使用大小为6的数组C[6]表示为桶,下标对应分数,c[6]内存储的是对应考生的个数,只需要遍历一遍考生的成绩,就能得到c[6]的值,即c[0]:2,c[1]:0,c[2]:2,c[3]:3,c[4]:0,c[5]:1,明显得出分数为3的考生有3个,小于3分的考生有4个,所以成绩为3分的考生在排序之后的数组R[8]中,会保存下标4,5,6的位置
R[8]:blank blank blank blank 3 3 3 blank
0 1 2 3 4 5 6 7
如何计算出每个分数的考生在有序数组中对应的存储位置?
对C[6]数组顺序求和,c[6]存储的数据就会变成下面的样子,C[k]里存储小于等于分数k的考生个数
c[6]: 2 2 4 7 7 8
0 1 2 3 4 5
从后到前依次扫描数组A,比如当扫描到3时,可以从数组C中取出下标为3的值7,即包括自己在内,分数小于等于3的考生有7个,也就是说3是数组R中的第7个元素,即下标为6的位置,当3放入到数组R中,小于等于3的元素就只剩下6个了,所以相应的c[3]-1 =6,以此类推,当扫描到第2个分数为3的考生的时候,就会把它放入数组R中的第6个元素的位置(即下标为5的位置),当扫描完整个数组A后,数组R内的数据就是按分数从小到大排列的
//计数排序,a是数组,n是数组大小,假设数组中存储的都是非负整数
public void countingSort(int[] a ,int n){
if(n <= 1) return;
//查找数组中数据的范围
int max = a[0];
for(int i =1 ;i < n;++i){
if(max < a[i]){
max = a[i]; //求成绩的最大值
}
}
int[] c = new int [max + 1];//申请一个计数数组c,下标大小[0,max] //max为最大数组值,申请一个max+1大小的数组
for(int i=0;i<= max;++i){ //初始化数组都为0
c[i] = 0;
}
//计算每个元素的个数,放入c中
for(int i =0;i <= n ;++i){ //将8个成绩都变成元素的个数,即每个下标都是成绩,c[a[i]]是每个成绩的考生个数
c[a[i]]++;
}
//依次累加
for(int i = 1; i <= max;++i){ //6个成绩,累加
c[i] = c[i-1] +c[i];
}
//临时数组r,存储排序之后的结果
int[ ] r = new int[n];
//计算排序的关键步骤
for(int i = n-1;i >= 0 ;--i){
int index = c[a[i]]-1;
r[index] = a[i];
c[a[i]]--;
}
//将结果拷贝给a数组
for(int i = 0;i<n;++i){
a[i] = r[i]
}
}
利用另一个数组来计数的实现方式就是叫做计数排序的原因
计数排序只能用于数据范围不大的场景中,如果数据范围k比要排序的数据n大很多,不适合用计数排序,而且如果要排序的数据是其他类型的,要将在其不改变相对大小的情况下,转化为非负整数
比如,考生的成绩精确到小数点后一位,需要将所有分数都先乘以10,转化为整数,然后放到9010个桶内
基数排序(Radix Sort)
加入我们有10W个手机号码,希望这10W个手机号码从小到大排序
假如要比较两个手机号码a,b的大小,如果前面几位中,a手机号码已经比b大了,后面几位就不用看了。先按照最后一位来排序手机号码,然后再按照倒数第二位重新排序,以此类推,经过11次排序之后,手机号码都有序
这样按照每位来排序的排序算法要是稳定的,否则这个实现思路是不正确的
根据每一位来排序,可以用桶排序或者计数排序,时间复杂度是O(n),如果要排序的数据有K位,就需要k次桶排序或者计数排序,总时间复杂度为O(k*n),手机号码排序中k最大是11,所以基数排序时间复杂度近似于O(n)
实际上,要排序的数据并不是等长的,单词最短的只有1个字母,最长的有45个,基数排序怎么排列?
可以将所有的单词补齐到相同长度,位数不够的可以在后面补’0’,根据ASCII码,所有字母都大于0,所以补‘0’并不影响
基数排序对要排序的数据是有要求的,需要可以分割出独立的‘位’来比较,而且位之间有递进关系,如果a数据的高位比b数据大,那么剩下的低位都不用比较了,除此之外,每一位的数据范围不能太大,要可以用线性排序算法来排序
如何根据年龄给100w用户数据排序?
根据年龄给100W用户排序,类似根据成绩个100W考生排序,假设年龄范围为1到120,可以遍历这100W用户,根据年龄将其划分到120个桶内,然后依次顺序遍历这120个桶中的元素,这样得到了按照年龄排序的100W用户数据
假设我们现在需要对D,a,F,B,c,A,z这个字符串进行排序,要求将其中的所有小写字母都排在大写字母的前面,但小写字母内部和大写字母内部不要求有序,比如经过排序之后a,c,z,D,F,B,A,假设字符串中存储的不仅仅有字母,还有数字,要将小写字母放到前面,大写字母放到后面,数字放中间,不用排序算法,怎么办?
包含数字就是一个荷兰国旗问题
荷兰国旗问题可参考: https://www.jianshu.com/p/356604b8903f
(1)用两个指针a,b。 a指针从头开始往后遍历,遇到大写字母就停下,b从后往前遍历,遇到小写字母就停下,交换a,b对应的元素,重复上述过程,直到a,b指针相交
(2)可以先将数据分为小写字母和非小写字母两大类,进行如上交换后再在非小写字母区间内分为数字和大写字母做同样处理
基数排序详细图解以及为什么从低位开始
来源: https://blog.csdn.net/qq_43665697/article/details/99425086
1.为什么不从高位开始?
首先基数排序是对桶排序的一种扩展用的是10个队列本身就挺消耗空间的如果从高位开始你还要利用递归的思想对每个队列在进行排序在准备10个队列 以此类推直到一个数一个队列为止 这样虽然符合基数排序的规则但是会大大浪费空间
还有一种办法就是从高位开始然后对每个队列进行排序 大概意思就是遍历10个队列 对每个队列里边的元素进行某种算法排序 这样每组都是有序的 整体又有序 最后肯定是一个有序的数组了 但是这样不符合基数排序的规则
综上 不是高位开始不行 而是浪费空间或者更复杂所以从底位开始确实比高位要好
2.为什么从低位开始对个位十位百位等等等排完序最后数组就有序了?
首先我对个位排完序 个位就是从小到大排列的 在此基础上对十位进行排序 注意是在此基础上在对上一位进行排序 如果十位相同 此时决定2个数顺序就是由个位决定了 而个位已经排好序了所以 此时十位相同的2个数顺序肯定就没错了 以此类推 最后数组肯定是排序正确的有序数组了
准备10个队列 因为不管哪一位都是从0到9的麻所以要准备10个队列 然后对位数不够的元素前边补0 假如 最大的数是3位 假如有个元素是4 那么就当004算 (补0只是为了方便演示 实际上算法是对当前位取余 假如4 对十位取余 就相当于 0.4%10 =0 )
先对个位进行排序 个位是0就放队列0中 个位是1就放队列1中 最后得到的是一个个位有序的数组
然后在对个位有序的数组进行十位排序 以此类推得到一个有序的数组
图片来源 https://www.cnblogs.com/l199616j/p/10738568.html
荷兰国旗问题
给定一个整数数组,给定一个值K,这个值在原数组中一定存在,要求把数组中小于K的元素放到数组的左边,大于K的元素放到数组的右边,等于K的元素放到数组的中间,最终返回一个整数数组,其中只有两个值,分别是等于K的数组部分的左右两个下标值。
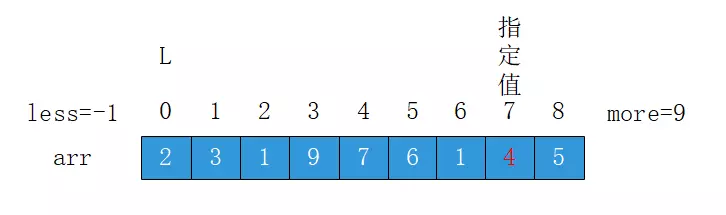
例如,给定数组:[2, 3, 1, 9, 7, 6, 1, 4, 5],给定一个值4,那么经过处理原数组可能得一种情况是:[2, 3, 1, 1, 4, 9, 7, 6, 5],需要注意的是,小于4的部分不需要有序,大于4的部分也不需要有序,返回等于4部分的左右两个下标,即[4, 4]
less 用于记录小于 4 的区域的右下标,初始为-1,代表不存在
more 用于记录大于 4 区域的左下标,初始为9,代表不存在
L 用于正在遍历的元素的下标,初始值为0
从 arr[L] 即 arr[0] 开始遍历数组
- 如果 arr[L] > 4, 交换 arr[++ less] 和 arr[L++] 的值
- 如果 arr[L] < 4, 交换 arr[–more] 和 arr[L] 的值
- 如果 arr[L] = 4, 不交换,L++,直接遍历下一个值
当 L >= more,退出循环。
来源:CSDN
作者:ywangjiyl
链接:https://blog.csdn.net/ywangjiyl/article/details/103480175