452. 用最少数量的箭引爆气球

ID: 452
TITLE: 用最少数量的箭引爆气球
TAG: Java，Python，C++，贪心算法

方法：贪心算法

贪心算法一般用来解决需要 “找到要做某事的最小数量” 或 “找到在某些情况下适合的最大物品数量” 的问题，且提供的是无序的输入。

贪心算法的思想是每一步都选择最佳解决方案，最终获得全局最佳的解决方案。

标准解决方案具有 $\mathcal{O}(N \log N)$ 的时间复杂度且由以下两部分组成：

思考如何排序输入数据（ $\mathcal{O}(N \log N)$ 的时间复杂度）。
思考如何解析排序后的数据（ $\mathcal{O}(N)$ 的时间复杂度）

如果输入数据本身有序，则我们不需要进行排序，那么该贪心算法具有 $\mathcal{O}(N)$ 的时间复杂度。

如何证明你的贪心思想具有全局最优的效果：可以使用反证法来证明。

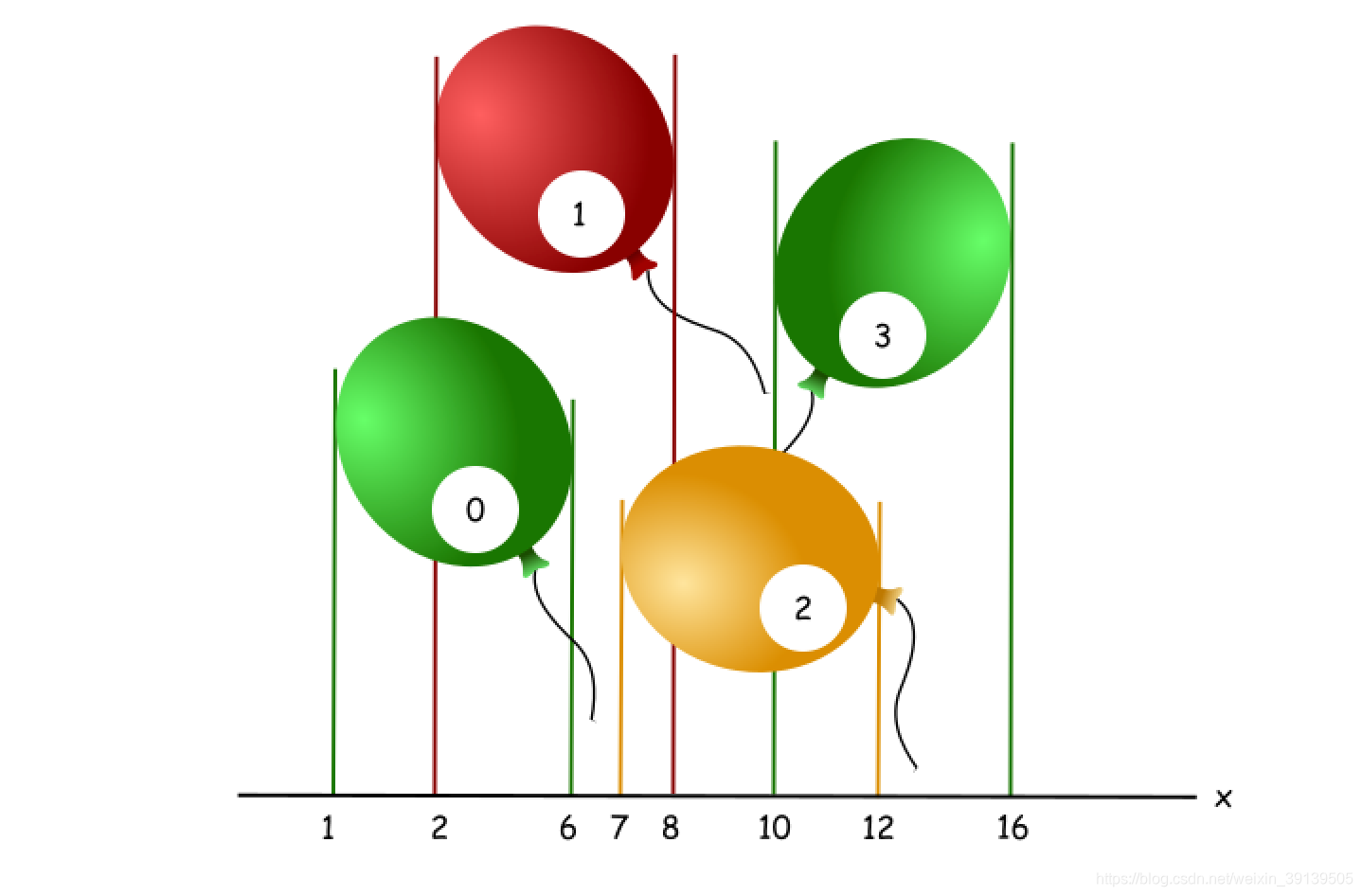
让我们来看下面的气球箭的组合情况。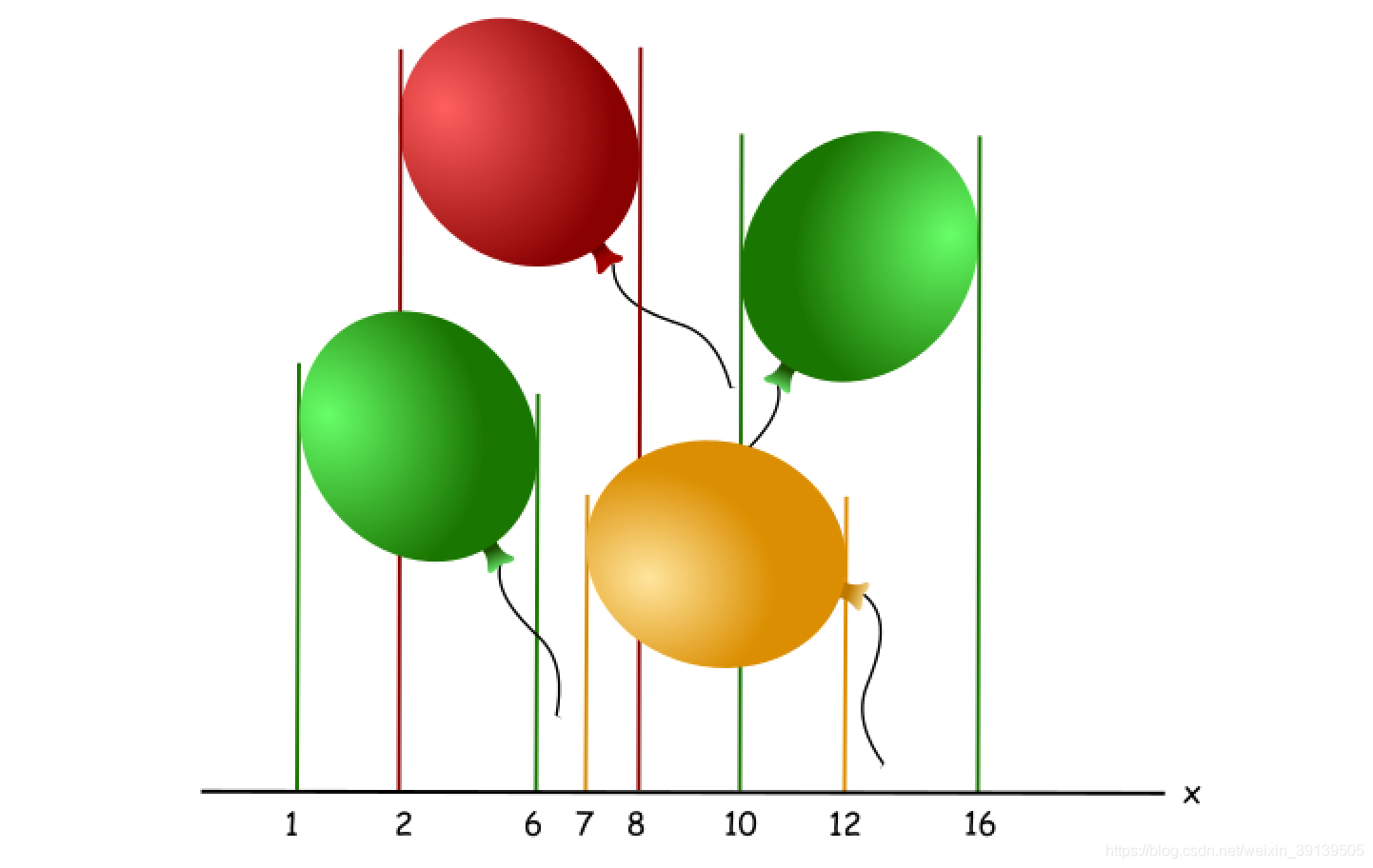
在这里插入图片描述
很明显我们使用两支箭就能使全部气球引爆，我们借助此例子来思考如何用贪心算法的思想来计算结果。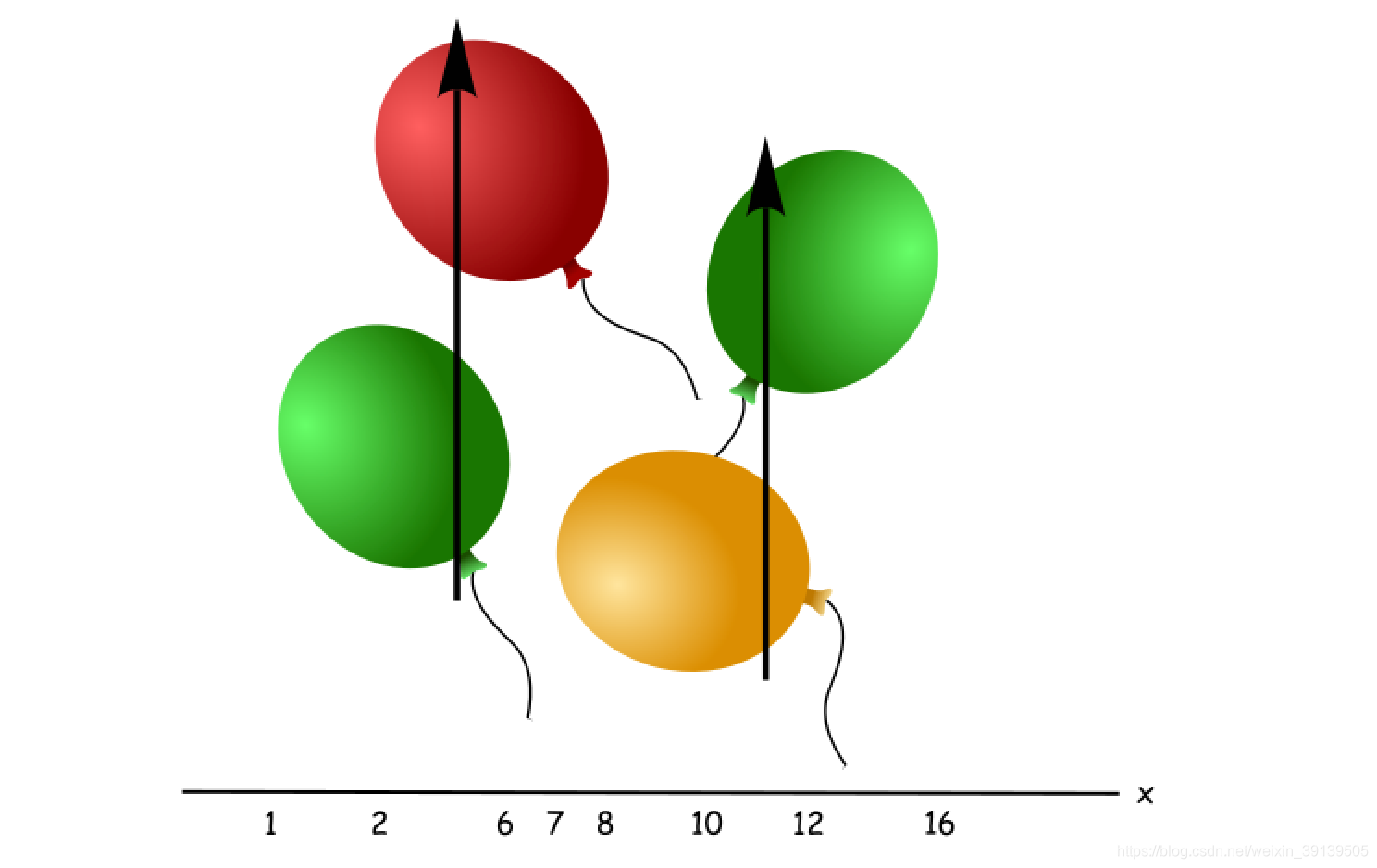

让我们根据气球的结束坐标进行排序，然后一个个进行检查。第一个气球是标有 0 的绿色气球，它的结束坐标是 6。

其他的气球有两种情况：

开始坐标小于 6，例如红色气球，它可以与 0 气球一起被一支箭引爆。
开始坐标大于 6，例如黄色气球，它不可以与 0 气球被一支箭引爆，因此需要增加箭的数量。

这代表了我们可以跟踪气球的结束坐标，若下个气球开始坐标在当前气球的结束坐标前，则我们可以用一支箭一起引爆；若下个气球的开始坐标在当前气球的结束坐标后，则我们必须增加箭的数量。并跟踪下个气球的结束坐标。

算法：

根据 x_end 将气球进行排序。
初始化 first_end 为第一个气球结束的坐标 points[0][1]。
初始化箭的数量 arrows = 1。
遍历所有的气球：
- 如果气球的开始坐标大于 first_end：
  - 则增加箭的数量。
  - 将 first_end 设置为当前气球的 x_end。
返回 arrows。

class Solution:
    def findMinArrowShots(self, points: List[List[int]]) -> int:
        if not points:
            return 0
        
        # sort by x_end
        points.sort(key = lambda x : x[1])
        
        arrows = 1
        first_end = points[0][1]
        for x_start, x_end in points:
            # if the current balloon starts after the end of another one,
            # one needs one more arrow
            if first_end < x_start:
                arrows += 1
                first_end = x_end
        
        return arrows

class Solution {
  public int findMinArrowShots(int[][] points) {
    if (points.length == 0) return 0;

    // sort by x_end
    Arrays.sort(points, new Comparator<int[]>() {
      @Override
      public int compare(int[] o1, int[] o2) {
        return o1[1] - o2[1];
      }
    });

    int arrows = 1;
    int xStart, xEnd, firstEnd = points[0][1];
    for (int[] p : points) {
      xStart = p[0];
      xEnd = p[1];
      // if the current balloon starts after the end of another one,
      // one needs one more arrow
      if (firstEnd < xStart) {
        arrows++;
        firstEnd = xEnd;
      }
    }

    return arrows;
  }
}

class Solution {
  public:
  int findMinArrowShots(vector<vector<int>>& points) {
    if (points.size() == 0) return 0;

    // sort by x_end
    sort(begin(points), end(points),
         [](const vector<int> &o1, const vector<int> &o2) {
      return (o1[1] < o2[1]);
    });

    int arrows = 1;
    int xStart, xEnd, firstEnd = points[0][1];
    for (auto p : points) {
      xStart = p[0];
      xEnd = p[1];
      // if the current balloon starts after the end of another one,
      // one needs one more arrow
      if (firstEnd < xStart) {
        arrows++;
        firstEnd = xEnd;
      }
    }
    return arrows;
  }
};

复杂度分析

时间复杂度： $\mathcal{O}(N \log N)$ 。因为对输入数据进行了排序。
空间复杂度： $\mathcal{O}(1)$ ，仅仅使用了常数空间。

来源：CSDN

作者：陈乐乐happy

链接：https://blog.csdn.net/weixin_39139505/article/details/103495306

标签

时间复杂度