归并排序、快速排序

归并排序：使用的是分而治之的思想，将大问题分解成小的子问题来解决，比如用归并排序来对一个数组进行排序，首先把数组从中间分成前后两部分，然后对它们分别排序，再将排好序的两部分合并在一起，这样整个数组就有序了。

任何情况下都是O(nlogn)，在合并两个有序数组为一个有序数组时，需要借助额外的存储空间，n/2，n/4，…，1 ，所以空间复杂度为 O(n)。稳定。

    public void mergeSort(int[] a) {
        int n = a.length;
        if (n <= 1) {
            return;
        }
        merge(a, 0, n - 1);
    }

    private void merge(int[] a, int l, int r) {
        if (l >= r) {
            return;
        }
        int mid = l + ((r - l) >> 1);
        merge(a, l, mid);
        merge(a, mid + 1, r);
        mergeTwo(a, l, mid, r);
    }

    private void mergeTwo(int[] a, int l, int mid, int r) {
        int[] tmp = new int[r - l + 1];
        int i = l;
        int j = mid + 1;
        int k = 0;
        while (i <= mid && j <= r) {
            if (a[i] <= a[j]) {
                tmp[k++] = a[i++];
            } else {
                tmp[k++] = a[j++];
            }
        }
        while (i <= mid) {
            tmp[k++] = a[i++];
        }
        while (j <= r) {
            tmp[k++] = a[j++];
        }
        for (int m : tmp) {
            a[l++] = m;
        }
    }

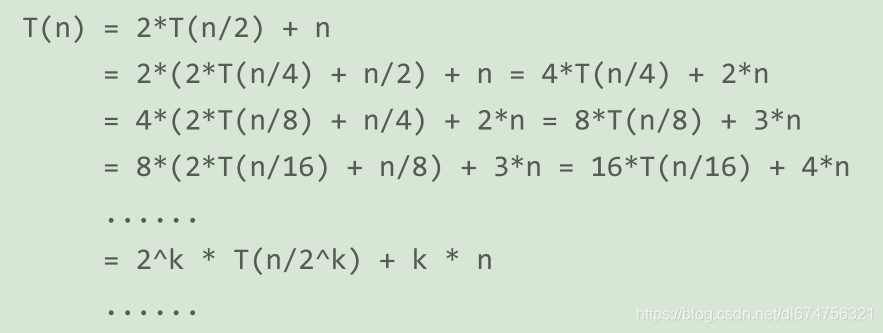
当划分到只有一个元素时，也就是 n/2^k = 1 ，此时 k = logn ，所以最后 T(n) = nlogn 。

  

快速排序：使用的是分而治之的思想，将大问题分解成小的子问题来解决，比如用快速排序来对一个数组进行排序，首先选择一个基准值，然后遍历数组，将小于基准值的放在左边，大于基准值的放在右边，基准值放在中间，这样数组就被分成了三部分，然后在用递归的思想对小于基准值的部分和大于基准值的部分再进行一次比较划分，每一次可以确定其中一个元素的最终位置。

O(nlogn)，O(1)，不稳定。当数组中原来的元素已经有序时，快排的时间复杂度就会退化成O(n)，原因是：快排是通过选择一个元素作为基准值来进行分区，如果有序，那么每次分区都要扫描 n/2 个元素，于是需要进行约n次分区操作才能完成快排，所以时间复杂度就为 O(n) 了。

    public static void quickSort(int[] a, int first, int last) {
        if (first >= last || a == null || a.length <= 1) {
            return; //每一趟结束的条件
        }
        int i = first;
        int j = last;
        int index = a[first]; // 以第一个数49作为基准
        while (i != j) {
            //从右往左扫描，找到第一个比49小的元素，并交换
            while (i < j && a[j] >= index) {
                j--;
            }
            //找到之后交换
            if (i < j) {
                a[i++] = a[j];
            }
            //从左往右扫描，找到第一个比49大的元素，并交换
            while (i < j && a[i] < index) {
                i++;
            }
            //找到之后交换
            if (i < j) {
                a[j--] = a[i];
            }
        }
        a[i] = index;

        quickSort(a, first, i - 1); // 对低子表进行递归排序
        quickSort(a, i + 1, last); // 对高子表进行递归排序
    }

来源：CSDN

作者：喵了个咪的回忆丶

链接：https://blog.csdn.net/dl674756321/article/details/103490274