一、算法简介

k邻近算法( k-nearest neighbors )，即 KNN 算法。

KNN是一种基于实例学习( instance-based learning )，或者所是将所有计算推迟到分类之后的惰性学习( lazy learning )的一种算法，KNN可以说是最简单的分类算法之一，同时，它也是最常用的分类算法之一，注意KNN算法是有监督学习中的分类算法。

二、算法原理

KNN算法的思路是：如果一个样本在特征空间中的 k 个最相似(即特征空间中最邻近)的样本中的大多数属于某一个类别，则该样本也属于这个类别。通常 K 是不大于20的奇数。

用一句我们中国的古话来说，就是“近朱者赤，近墨者黑。”

举个例子：

一只小鹰出生怎么判断自己是一只鹰还是一只鸡呢？

如下图，我们假设绿色代表这只小鹰。红色代表鸡，蓝色代表鹰。

它睁开眼看了一下周围3只动物，两只是鸡，一直是鹰。他就把自己分类为鸡。当他看的比较远的时候，他看到了周围5只动物。发现三只是鹰，两只是鸡。他就把自己分类为鹰。

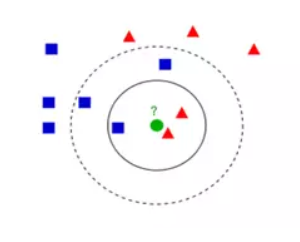
从上面的例子中，我们可以看出该算法涉及3个主要因素：训练集、距离或相似的衡量、k的大小。

关于距离的测量方式有多种，这里只介绍两种。

欧氏距离这种测量方式就是简单的平面几何中两点之间的直线距离。

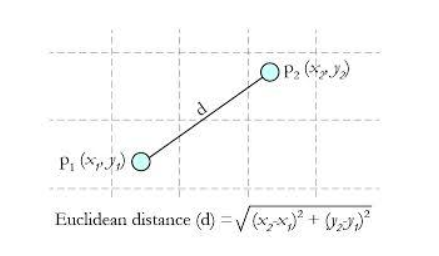
并且这种方法可以延伸至三维或更多维的情况。它的公式可以总结为:

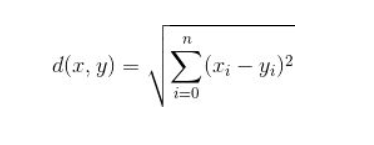
曼哈顿距离顾名思义，城市街区的距离就不能是点和点的直线距离，而是街区的距离。如棋盘上也会使用曼哈顿距离的计算方法：

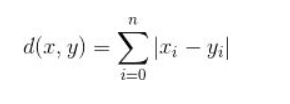
这样我们就明白了如何计算距离，通常KNN算法中使用的是欧式距离。KNN算法最简单粗暴的就是将预测点与所有点距离进行计算，然后保存并排序，选出前面K个值看看哪些类别比较多。

为什么KNN使用欧式距离而不是曼哈顿距离？

KNN不用曼哈顿距离，因为它只计算水平或垂直距离，有维度的限制。另一方面，欧氏距离可用于任何空间的距离计算问题。因为，数据点可以存在于任何空间，欧氏距离是更可行的选择。例如：想象一下国际象棋棋盘，象或车所做的移动是由曼哈顿距离计算的，因为它们是在各自的水平和垂直方向做的运动。

通过小鸡和老鹰的案例我们知道了，KNN算法的关键点K值选取很重要。那么，K究竟应该怎么取值呢？

答案是通过交叉验证（将样本数据按照一定比例，拆分出训练用的数据和验证用的数据，比如6：4拆分出部分训练数据和验证数据），从选取一个较小的K值开始，不断增加K的值，然后计算验证集合的方差，最终找到一个比较合适的K值。

经验规则：k一般低于训练样本数的平方根

简单，易于理解，无需建模与训练，易于实现；

适合对稀有事件进行分类；

适合与多分类问题，例如根据基因特征来判断其功能分类，kNN比SVM的表现要好。

惰性算法，内存开销大，对测试样本分类时计算量大，性能较低；

可解释性差，无法给出决策树那样的规则。

来源：oschina

链接：https://my.oschina.net/u/3938912/blog/3142177

标签