常见激活函数，及其优缺点 - 面试篇

废话不多说，直接开问。

问：什么是激活函数？
在多层神经网络中，上层节点的输出和下层节点的输入之间具有一个函数关系，这个函数称为激活函数。

问：激活函数有什么用？
如果没有激励函数，在这种情况下你每一层节点的输入都是上层输出的线性函数，无论你神经网络有多少层，输出都是输入的线性组合，相当于没有隐藏层，网络的学习能力有限。
深度学习最主要的特点就是：多层，非线性。 多层为了能够学习更多的东西；没有非线性，多层和单层没什么区别，就是简单的线性组合，连异或都解决不了。
感兴趣的可以看这篇文章：为什么神经网络需要解决多层和非线性问题

问：介绍一下你熟悉的激活函数？特点，优缺点

sigmoid函数

$f(z) = \frac{1}{1+e^{-z}}$
特点：
它能够把输入的连续实值变换为0和1之间的输出，特别的，如果是非常大的负数，那么输出就是0；如果是非常大的正数，输出就是1.
导数曲线：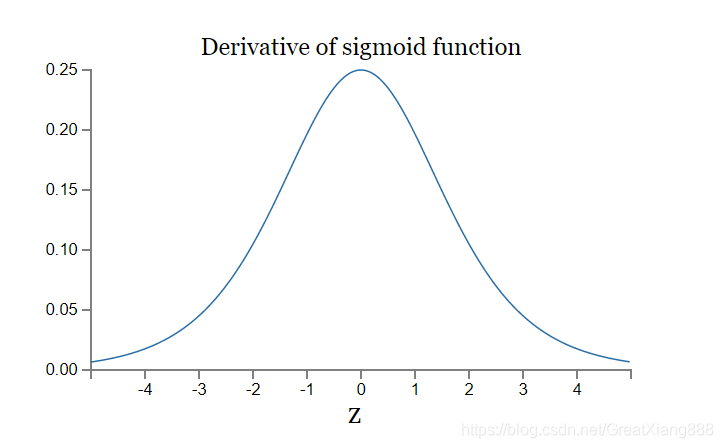

缺点：

1. 容易导致梯度消失。
   如果我们初始化神经网络的权值为 [0,1]之间的随机值，由反向传播算法的数学推导可知，梯度从后向前传播时，每传递一层梯度值都会减小为原来的0.25倍，如果神经网络隐层特别多，那么梯度在穿过多层后将变得非常小接近于0，即出现梯度消失现象。
   （这里有个坑，面试官可能听你提起反向传播，然后问你：什么是反向传播？会推导公式吗？查看我另一篇博客：反向传播，及其公式推导 - 面试篇）
   
   问：梯度消失和梯度爆炸？改进方法。
   解决梯度爆炸：
   a.可以通过梯度截断。通过添加正则项。
   解决梯度消失：
   a.将RNN改掉，使用LSTM等自循环和门控制机制。
   b.优化激活函数，如将sigmold改为relu
   c.使用batchnorm
   d.使用残差结构
   可以看这篇文章 详解机器学习中的梯度消失、爆炸原因及其解决方法

2. Sigmoid 的输出不是0均值（即zero-centered）。
   这会导致后一层的神经元将得到上一层输出的非0均值的信号作为输入。
   结果：那么对w求局部梯度则都为正，这样在反向传播的过程中w要么都往正方向更新，要么都往负方向更新，导致有一种捆绑的效果，使得收敛缓慢。（我没太看明白，点击看原文这里，或者这里）
   我的理解是，像relu函数，导数为1，输入正数输出则为正数，输入负数输出则为负数，正负情况都有。而若经过sigmoid后只有正数了，如果损失函数为二次函数$y=x^{2}$,那只能从右边进行梯度下降了，左边那一块没有用上。（梯度下降是考点，引申 sgd，batch-sgd，优缺点； 其他优化器等 查看我另一篇博客：梯度下降法，优化器及优缺点 - 面试篇）
   （面试官看你说了数据的偏移，不是0均值，可能会问你，你会哪些normalization[规范化]方法？batch norm，layer norm[头条算法岗问过]会不会？
   可以看我另一篇博客：normalization知识点总结 - 面试篇 或者看这篇 BatchNormalization…等总结）
   不过这个缺点相比梯度消失来说比较小。

3. 解析式中含有幂运算，计算机求解时相对来讲比较耗时。对于规模比较大的深度网络，这会较大地增加训练时间。
   像word2vec中为了解决softmax计算慢的问题，有3钟解决办法。1，如果精度要求不高，可以用表格法先计算[-x,x]分为n份对应的值，存在数组中，到时候可以直接查表。2，分层次的softmax，将叶子节点构建成哈夫曼树。 3，负采样技术。(以后有机会再展开，自己都觉得太多太乱了)
   （引申考点：word2vec，哈夫曼树算法[手写，复杂度]）
   
   

tanh函数

$tanh(x) = \frac{e^{x}-e^{-x}}{e^{x}+e^{-x}}$
特点：和sigmoid差不多，但值域为[-1,1]
解决了Sigmoid函数的不是zero-centered输出问题。
梯度消失和幂运算的问题仍然存在。
实际上，tanh和sigmoid函数存在变换关系：
$tanh(\frac{x}{2}) = 2*sigmoid(x)-1$

relu函数

$relu(x)=max(0,x)$
优点：

1. 解决了梯度消失问题
2. 计算速度非常快，只需要判断输入是否大于0
3. 收敛速度远快于sigmoid和tanh，因为这两个梯度最大为0.25，而relu为1

缺点：

1. 输出不是zero-centered
2. Dead ReLU Problem，指的是某些神经元可能永远不会被激活，导致相应的参数永远不能被更新。有两个主要原因可能导致这种情况产生: (1) 非常不幸的参数初始化，少见 。例如w初始化全部为一些负数。(2) learning rate太高导致在训练过程中参数更新太大，不幸使网络进入这种状态。解决方法是可以采用Xavier初始化方法，以及避免将learning rate设置太大或使用adagrad等自动调节learning rate的算法。
   （问：初始化你会哪几种方法？[头条算法岗面试]可以看我另一篇博客：深度学习初始化的方法 - 面试篇 ）
   这和dropout的实现方法可以类比，可以看我另一篇博客：防止过拟合的方法，及dropout原理 - 面试篇
3. 原点不可导
   
   

leaky relu函数

$f(x)=max(\alpha x,x)$
比如取$\alpha=0.01$，可以改善relu中x<0部分的dead问题。

ELU (Exponential Linear Units) 函数

$f(x)=\left\{ \begin{aligned} x , if \,\,\,x&gt;0 \\ \alpha (e^{x}-1),\,otherwise \\ \end{aligned} \right.$
优点：
不会有Dead ReLU问题
输出的均值接近0，zero-centered
缺点：
计算量稍大
原点不可导

gelu函数

论文链接：https://arxiv.org/pdf/1606.08415.pdf
参考 这里 和 这里
bert中使用的激活函数，作者经过实验证明比relu等要好。
$GELU(x) = xP(X \leq x) = x\Phi (x).$
这里$\Phi (x)$是正太分布的概率函数。可以使用参数化的正太分布$\N(\mu,\sigma)$, 然后通过训练得到$\mu$,$\sigma$。
(我自己的一点想法：只要不断向relu函数形状去拟合，可以得到参数。不知道具体怎么做的。)

近似计算公式：
$GELU(x) = 0.5x(1 + tanh[\sqrt{2/\pi }(x + 0.044715x^3)])$
比较：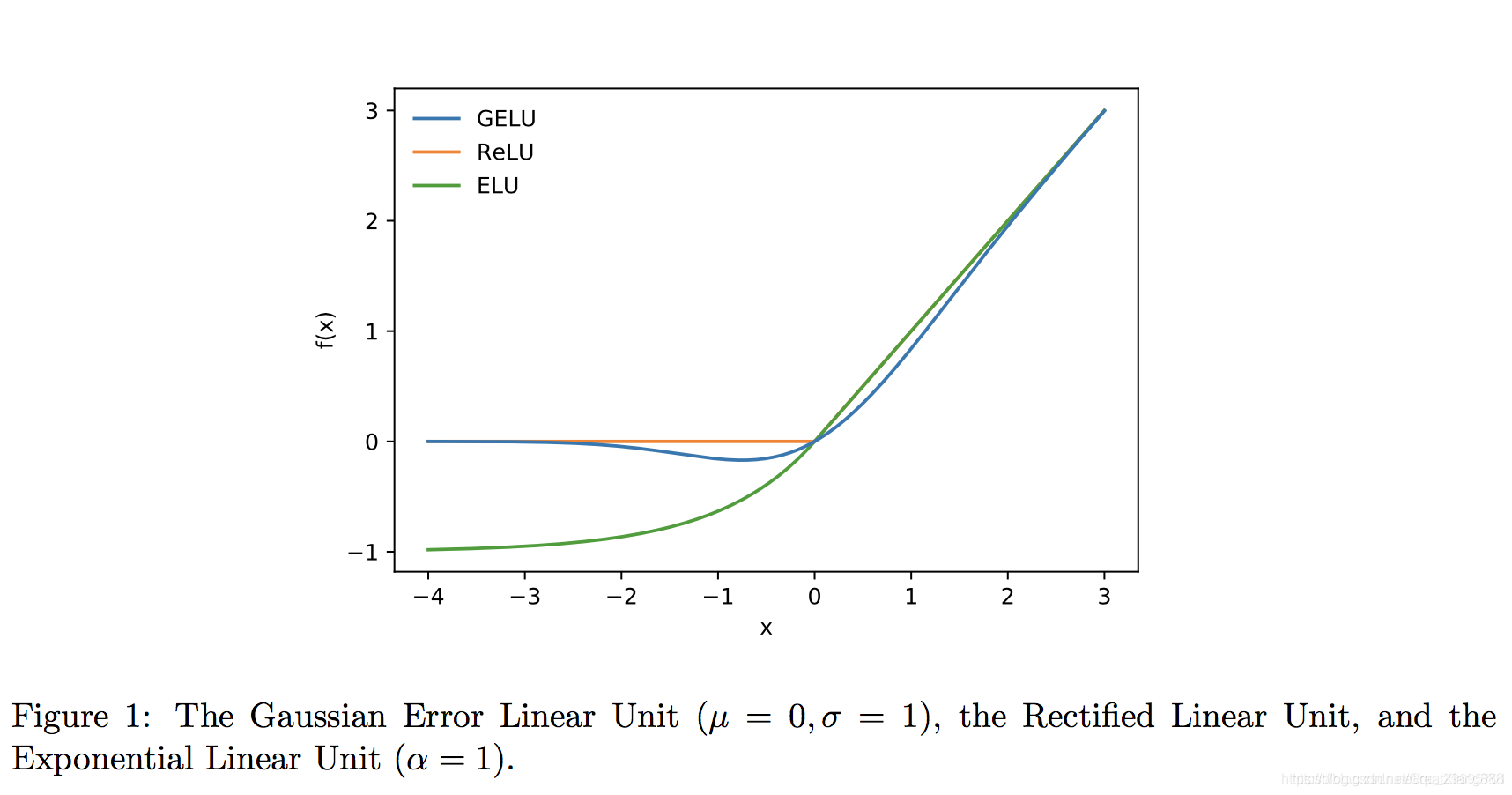

效果：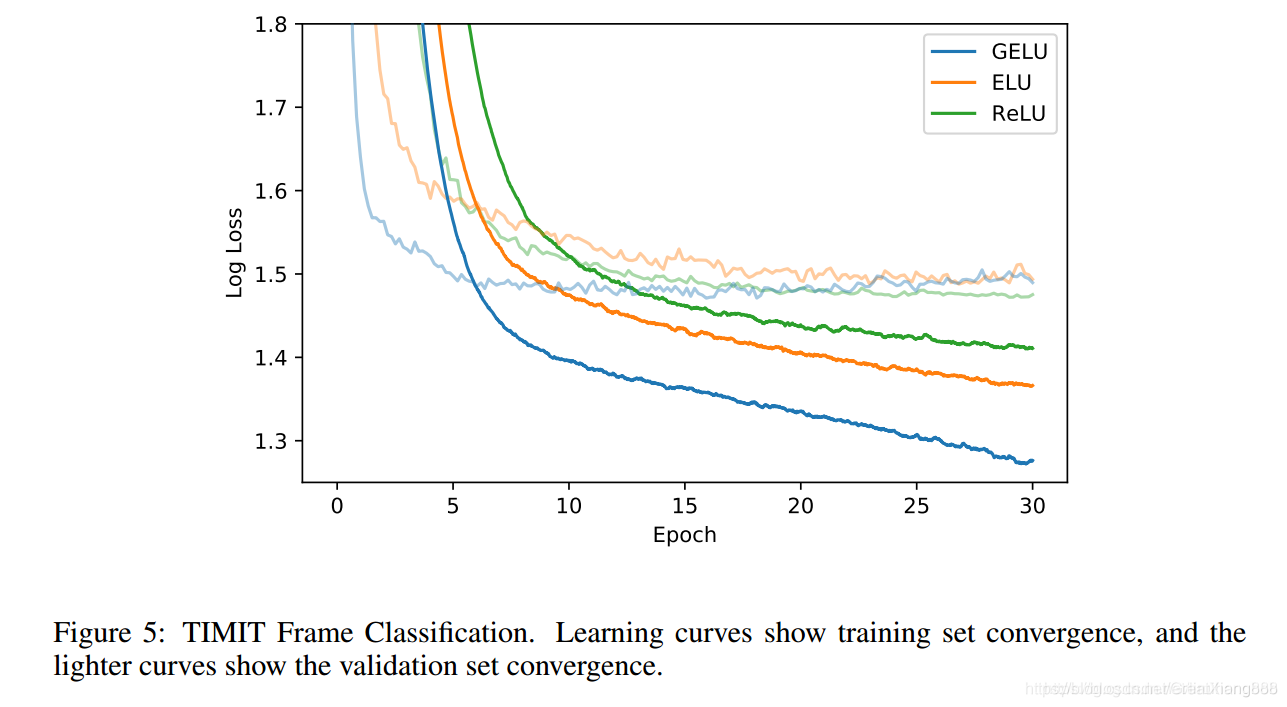

优点：
原点可导
不会有Dead ReLU问题

参考资料：
常见激活函数

来源：https://blog.csdn.net/GreatXiang888/article/details/99296607