leetcode98.验证二叉搜索树

给定一个二叉树，判断其是否是一个有效的二叉搜索树。

假设一个二叉搜索树具有如下特征：

节点的左子树只包含小于当前节点的数。
节点的右子树只包含大于当前节点的数。
所有左子树和右子树自身必须也是二叉搜索树。
示例 1:

输入:
    2
   / \
  1   3
输出: true

示例 2:

输入:
    5
   / \
  1   4
     / \
    3   6
输出: false
解释: 输入为: [5,1,4,null,null,3,6]。
     根节点的值为 5 ，但是其右子节点值为 4 。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/validate-binary-search-tree
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

完整代码

特别说明：并不是左右子树都是二叉搜索树，最终结果就是二叉搜索树

举例：
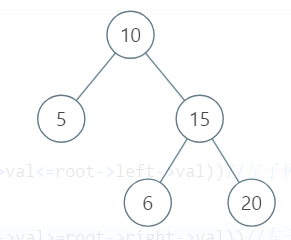
[10,5,15,null,null,6,20]

左右子树的确是二叉搜索树，但是这棵树不是二叉搜索树。
那么如何改进呢？
其实二叉搜索树的中序遍历是一个递增的序列，只需稍微修改下中序遍历的递归算法就可以，只要让上一次遍历的节点的值小于当前遍历节点的值就可以，否则就不是二叉搜索树。
说明：需要特别记录下上一次遍历的节点的值是多少

这里有个坑
初始情况：int preval=INT_MIN;会导致只有一个节点的二叉树且该节点的值是INT_MAX的情况返回false，其实应该是true，所以我们将preval定义成Long型，且最小值是LONG_MIN

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    long preval=LONG_MIN;
    bool isValidBST(TreeNode* root) {
        if(root==NULL)
            return true;
        bool lb,rb;
        lb=isValidBST(root->left);
        if(!lb||preval>=root->val)//左子树不是二叉搜索树或者根的值小于上一次遍历的节点的值
            return false;
        preval=root->val;
        rb=isValidBST(root->right);
        return rb;       
    }
};

同样，使用中序遍历的非递归形式也可以实现

来源：CSDN

作者：qq_31672701

链接：https://blog.csdn.net/qq_31672701/article/details/103481150

标签

二叉搜索树